Рисунки по координатам для начальной школы

Содержание

Слайд 1

МОУ «Береговская СОШ»
Денисова Ольга Фёдоровна
х
y
0
1

1

1
Слайд 2

Цели урока:
познакомить учащихся с понятием «Координатная плоскость»;
показать на примерах использование понятия координатная плоскость в других областях;
закрепить принцип построения точек на координатной плоскости.
2
Слайд 3

Задачи

обучающие:
ввести понятие координатной плоскости;
сформировать умения учащихся строить точки на координатной плоскости;
сформировать умения учащихся определять координаты точек, построенных на координатной плоскости.
развивающие:
развитие логического и математического мышления, четкости и аккуратности выполнения.
воспитательные:
развитие интереса к предмету.

3
Слайд 4

4
Слайд 5

= 14
5
Слайд 6

= 4
= 14
6
Слайд 7

=18
= 14
= 4
7
Слайд 8

=21
= 14
= 4
=18
8
Слайд 9

=11
=18
= 14
= 4
=21
9
Слайд 10

=17
Составь слово
= 14
=11
=21
=18
= 4

10
Слайд 11

Французский философ, математики естествоиспытатель (1596 – 1650).
Происходил из старинного дворянского рода.
Основным достижением Декарта явился созданный им метод координат,
поэтому прямоугольную систему координат часто называют
декартовой системой координат
11
Слайд 12

Из истории математики

Термин «координаты» произошел от латинского слова ordinatus – «упорядоченный», а приставка co указывает на «совместность», так как координат обычно бывает две или более.
Идея координат возникла в древности. Прямоугольную сетку (палетку) использовали уже в Древнем Египте.
Координатный метод как метод математики был разработан независимо друг от друга выдающимися французскими математиками Пьером Ферма и Рене Декартом (XVII в.).
Термины «абсцисса», «ордината», «координаты», «функция» были введены в 80-х годах XVII в. Лейбницем.

12
Слайд 13

5ряд 7 место
5
7 ряд 5 место
7
Места в зрительном зале
13
Слайд 14

Чтобы найти свое место в зале,
сначала мы ищем свой ряд, затем своё место.
Чтобы определить свое место в зале, сначала мы находим свой ряд, затем своё место.
14
Слайд 15

Параллели и меридианы — это воображаемые линии на поверхности Земли, а широта и долгота — это их координаты, определяющие положение точек на поверхности Земли.
15
Слайд 16

16
Слайд 17

17
Слайд 18

И г р ы
каждая клетка на игровом поле определяется двумя координатами — буквой и цифрой
Слайд 19

Положение фигуры на шахматной доске определяется буквой и цифрой
19
Слайд 20

Координатная плоскость
У
Х
0
О- начало координат
4
5
1
2
3
-1
-3
-2
-4
1
2
3
6
-1
-2
Ось абсцисс
Ось ординат
I четверть
II четверть
III четверть
IV четверть
20
Слайд 21

Декартова система координат
У
Х
0
4
5
1
2
3
-1
-3
-2
-4
1
2
3
6
-1
-2
А

абсцисса
ордината

В
(5;0)
(-3; 2)
-3
-4
4
5

С
(0;-4)

Д
(0;5)
21
Слайд 22

0
Х
У
1
2
3
4
5
6
-1
-2
-3
-4
1
2
3
-1
-2

(4;2)

В
(6;-3)

С
(- 4;3)
А

D
(-3;-2)
-5
-6
4
5
6
7
7
-7

Е
(-7;0)

F
(1;7)
22
Слайд 23

1

2

3

4 5

6

7 Х

-7 -6 -5 -4 -3 -2 -1 0

У

5
4
3
2
1

-1
-2
-3
-4
-5
-6

М
(6;2)

Построение точек по координатам

М(6;2)
К(-5;-3)

К(-5;-3)
Р(0;-5)

Р(0;-5)
Слайд 24

24
Слайд 25

Х
У
2
1
5
3
4
6
7
8
9
10
11
12
0
1
2
3
4
5
6
7
8
9

1) 5;5
2) 8;8
3) 9;8
4) 11;6
5) 12;6
6) 12;7
7) 11;7
11;2
9) 9;2
10) 9;3
11) 10;3
12) 10;4
13) 7;4
14) 7;2
15) 5;2
16) 5;3
17) 6;3
18) 6;9
20) 7;8
19) 7;9
21) 2;8
22) 2;9
23) 3;9
24) 3;6
25) 4;5
соединить
Точки

25
Практическая работа
Слайд 26

медвежонок
26
Слайд 27

(0;2)
(1;2)
(1;1)
(2;0)
(2;-2)
(1;-3)
(2;-3)
(3;-2)
(4;-3)
(1;-4)
(0;-3)
(-1;-4)
(0;-5)
(-2;-5)
(-3;-4)
(-1,5;-4)
(-1;-3)
(-3;-3)
(-4;0)
(-2,5;-1)
(0;1)

(0;2)
(-3;0)
(-4;3)
(-4;5)
(-1;8)
(-1;7)
(1;7)
(2;5)
(3;6)
(2,5;4,5)
(3;4)
(2;4)
(2;3)
(1;2)
(4;2)
(3;0)
(1;2)
(-1;7)
глаз
(1;5)

Уточка

27
Слайд 28

(0;2)
(1;2)
(1;1)
(2;0)
(2;-2)
(1;-3)
(2;-3)
(3;-2)
(4;-3)
(1;-4)
(0;-3)
(-1;-4)
(0;-5)
(-2;-5)
(-3;-4)
(-1,5;-4)
(-1;-3)
(-3;-3)
(-4;0)
(-2,5;-1)
(0;1)

(0;2)
(-3;0)
(-4;3)
(-4;5)
(-1;8)
(-1;7)
(1;7)
(2;5)
(3;6)
(2,5;4,5)
(3;4)
(2;4)
(2;3)
(1;2)
(4;2)
(3;0)
(1;2)
(-1;7)
глаз
(1;5)

Уточка

28
Слайд 29

(9;2)
(-6;-1)
(-1;-1)
(1;8)
(2;6)
(3;8)
(4;5)
(6;4)
(5;3)
(7;1)
(7;2)
(8;2)
(8;-3)

(4;-4)
(4;-3)
(1;-1)
(3;-8)
(0;-8)
(-1;-5)
(-5;-4)
(-5;-8)
(-8;-8)
(-8;-1)
(-9;2)
глаз
(4;2)
Пёсик

29
Слайд 30

(9;2)
(-6;-1)
(-1;-1)
(1;8)
(2;6)
(3;8)
(4;5)
(6;4)
(5;3)
(7;1)
(7;2)
(8;2)
(8;-3)

(4;-4)
(4;-3)
(1;-1)
(3;-8)
(0;-8)
(-1;-5)
(-5;-4)
(-5;-8)
(-8;-8)
(-8;-1)
(-9;2)
глаз
(4;2)
Пёсик

30
Слайд 31

Посмотреть все слайды

Знакомство с координатными плоскостями

Введение

На этом предварительном уроке алгебры преподаватель математики Juni Genesis расскажет о координатной плоскости, о том, как ее использовать, и о некоторых важных терминах, которые необходимо знать при работе с координатными плоскостями.

Координатные плоскости важны для понимания, потому что они помогают нам научиться читать графики, понимать точки в пространстве и даже применять концепции в других предметах, таких как наука о данных и программирование!

Важный словарный запас

Чтобы понять координатные плоскости, начните с изучения или повторения этих ключевых терминов. По мере того, как вы будете больше работать с графиками и координатными плоскостями, эти понятия будут появляться регулярно.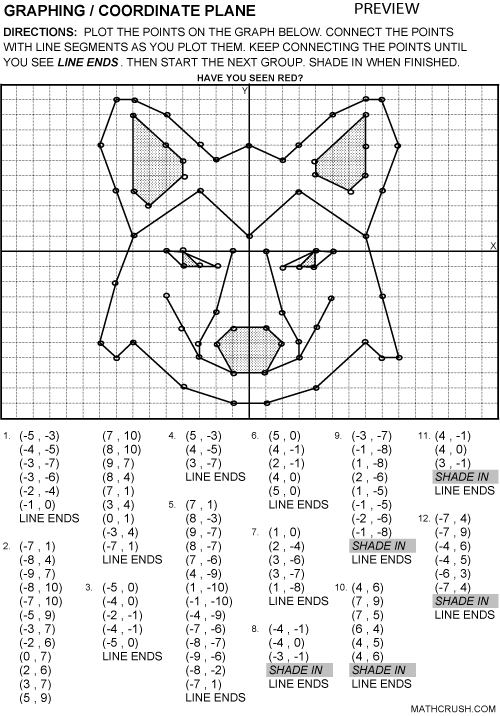

Посмотрите, как Бытие подробно объясняет каждый из этих терминов, используя примеры на координатной плоскости. Вы можете найти определения для справки, также написанные ниже.

Определения

Координатная плоскость

Особая плоскость, разделенная на четыре квадранта. Горизонтальная числовая линия, известная как ось x, и вертикальная числовая линия, известная как ось y, составляют координатную плоскость и пересекаются в начале координат (0,0).

Координаты

Числа на осях x и y, используемые для определения местоположения объектов на координатной плоскости. Обозначим координаты как (x, y).

Точка

Точное местоположение на плоскости.

Линейный сегмент

Линия создается при соединении двух точек A и B. Эта линия не проходит дальше ни одной из точек.

Средняя точка

Точка прямо в центре отрезка. Середина делит прямую на две равные половины.

Коллинеарность

Коллинеарность существует, когда две точки лежат на одной прямой.

Практические рабочие листы: проверьте свои знания

Если вы чувствуете себя комфортно с ключевыми терминами и концепциями, приведенными выше, попробуйте проверить себя с помощью рабочих листов Genesis Coordinate Planes !

Начните с разминки, чтобы закрепить свое понимание, повторите или потренируйте свой мозг, чтобы приступить к изучению математики в течение дня. Затем отточите свои навыки, ответив на более сложные вопросы, посвященные конкретным понятиям, изучаемым в этом уроке.

Вопросы для разминки: практика с координатными плоскостями
Сверла: сегменты в координатной плоскости (скоро!)

Нужна помощь или хотите продолжить обучение?

Надеемся, вам понравился урок Бытия о точках, линиях и координатных плоскостях! Этот урок входит в нашу учебную программу курса Pre-Algebra B.

Чтобы продолжать практиковаться или учиться, ознакомьтесь со всеми нашими учебниками по математике и программированию на странице «Домашние учебные ресурсы».

Genesis Luna окончила Техасский университет в Остине со степенью бакалавра искусств в области математики и сертификатом по медицинским специальностям.

Рисование с координатами

6 класс, 60-90 мин.

В упражнении «Рисование с координатами» учащиеся будут создавать свои собственные проекты, нанося пары координат на бумагу. Они обмениваются своим списком пар координат с партнером, который пытается воссоздать исходное изображение, чтобы увидеть, насколько точным был их алгоритм. Затем учащиеся вводят тот же список упорядоченных пар в веб-приложение Coordinate Drawer и изучают, как изменение точек и отражений влияет на их проекты.

Рассматриваемые темы

Определение координат точки
Отображение пар координат на координатной плоскости
Первичная концепция КИ: алгоритмическое мышление. Учащиеся эффективно пишут простой алгоритм со своей серией упорядоченных пар, и они начнут понимать, что компьютер, на котором работает их алгоритм (будь то их партнер или веб-приложение), понимает только точный алгоритм, который они ввели.

Студенты смогут

Создавайте художественные проекты, рисуя и управляя парами координат
Поймите, что компьютеры выполняют ту же последовательность шагов, которую мы вводим, даже если мы имели в виду что-то другое

Подготовка

Установите приложение Chrome Coordinate Drawer на устройства Chromebook учащихся (через консоль администратора Google), укажите ссылку, откуда они могут установить приложение Chrome, или укажите ссылку на веб-приложение. Если вы не используете Chromebook, вы должны использовать веб-приложение. Это занятие можно запустить и без приложения, если у вас нет устройств для учащихся.
Распечатайте рабочий лист на одной стороне, чтобы учащиеся могли совместно использовать вторую страницу независимо от первой.

Предлагаемая разбивка урока

Учащиеся могут самостоятельно проходить этот урок, но вы можете предложить или произвольно ввести следующие фрагменты:

5 минут – введение в задание
5-10 мин – Шаг 1: учащиеся проводят мозговой штурм и создают фигуру, используя только прямые линии
5 мин – Шаг 2: учащиеся строят чертежи и соединяют пары координат, чтобы воссоздать свой проект
10–20 мин. — Шаг 3: учащиеся определяют и перечисляют все пары координат, необходимые для воссоздания их проекта, помня, что порядок соединения каждой пары имеет решающее значение для алгоритма
10–20 мин — Шаг 4: учащиеся обмениваются вторыми страницами с партнером, и каждый пытается следовать алгоритму другого, нанося пары координат и соединяя их по порядку. Если учащиеся учатся самостоятельно, попросите двух учеников поменяться местами, как только они будут готовы двигаться дальше.
20-30 минут – учащиеся используют приложение Coordinate Drawer для воссоздания и управления своими проектами и/или создания новых проектов

Стандарты Common Core

CCSS.Math.Content.5.G.A.1 Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) совпадает с 0 на каждой линии и заданным точка на плоскости, расположенная с помощью упорядоченной пары чисел, называемой ее координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствуют (например, ось x и координата x, ось y и координата y).
CCSS.Math.Content.6.NS.C.6.B Понимать знаки чисел в упорядоченных парах как указывающие положения в квадрантах координатной плоскости; признать, что когда две упорядоченные пары различаются только знаками, положения точек связаны отражениями по одной или обеим осям.
CCSS.Math.Content.6.NS.C Поиск и расположение целых чисел и других рациональных чисел на горизонтальной или вертикальной числовой линейной диаграмме; найти и расположить пары целых чисел и других рациональных чисел на координатной плоскости.

Дистанционные курсы для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Ускоренный просмотр онлайн-лекций не мешает их пониманию

Время чтения: 3 минуты

Федеральный перечень учебников будет дополнен новыми учебниками

Время чтения: 3 минуты

В местах сдачи ЕГЭ будут применены антиковидные меры

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Сборник рисунков и фигур по координатам во всех стилях: от классических до современных

В искусстве создания рисунков и фигур по координатам существует множество стилей и направлений. Этот сборник представляет собой набор уникальных и разнообразных работ, выполненных с использованием координатной сетки.

Рисунки и фигуры, созданные по координатам, позволяют визуализировать сложные математические модели, геометрические формы или абстрактные идеи. Каждый рисунок представляет собой набор точек, соединенных линиями или кривыми, расположенных в пространстве с заданными координатами.

Каждый рисунок или фигура сопровождаются описанием, в котором указаны используемые координаты и особенности его создания. Это позволяет не только восхититься произведением искусства, но и изучить методы его создания и самостоятельно попробовать себя в этом увлекательном деле.

Сборник рисунков и фигур по координатам является полезным источником вдохновения и материалом для развития своих навыков искусства. Он поможет вам расширить ваши горизонты и открыть новые возможности в воплощении своих творческих идей.

python – Как лучше преобразовать координаты из холста tkinter

У меня есть простая система координат, которую я хочу отобразить на холсте tkinter. Когда пользователь щелкает ячейку, я хочу распечатать ее местоположение:

Каждая ячейка на холсте имеет высоту и ширину 15, поэтому, когда пользователь щелкает ячейку, соответствующее событие не является фактическим x и у координата.

Я имел в виду рисование на холсте прямоугольников разной высоты и ширины:

 х1 = 0
х2 = 0
у1 = 15
у2 = 15
для я в диапазоне (4):
    для я в диапазоне (8):
        canvas.create_rectangle(x1, x2, y1, y2, fill="синий",tags="playbutton", схема="зеленый")
        х1 += 15
        у1 += 15
    х1 = 0
    у1 = 15
    х2 += 15
    у2 += 15
Def щелкнул (* аргументы):
    х = аргументы. x
    у = аргументы.у
    печать (преобразовать_в_координаты (х, у)
canvas.tag_bind("кнопка воспроизведения","",нажато)

Тогда функция преобразования будет выглядеть примерно так:

 def convert_to_coord(x,y):
   convert_x = Нет
   convert_y = Нет
   если х >= 0 и х  15 и х  30 и х  45 и х

60 и х = 0 и у 15 и у 30 и у 45 и у

Мне интересно, есть ли лучший способ сделать это? Выглядит довольно неуклюже и много жестко запрограммированных значений для меня.

питон
ткинтер
координаты

Ради менее жестко запрограммированных вещей:

 dx = 15 # это может быть необязательным аргументом функции преобразования
xcells = 
для jx, xcell в перечислении (xcells):
   если x > jx*dx и x

то же самое для ycells, конечно.

Рисунки по координатам сложные — 76 фото

Рисунки на координатной плоскости сложные

Рисование по координатам

Сложное координатное рисование

Рисунки по координатам с координатами

Рисунки на миллиметровой бумаге

Рисунки на координатной плоскости сложные

Рисунки поткоординатам

Рисунки на миллиметровке

Прямоугольная система координат рисунок

Рисунок на координатной плоскости с координатами с координатами

Рисунки на координатной плоскости

Декартова система координат на плоскости рисунки

Ракета по координатным точкам

Рисунки на миллиметровой бумаге

Координатная плоскость программа

Рисунки на плоскости с координатами

Графический диктант по координатам

Координатная плоскость с координатами

Рисунки по клеточкам по координатам

Рисунок на координатной плоскости с координатами

Петух по координатам 1.

Рисунки на координатной плоскости

Ласточка по координатам

Попугай на координатной плоскости с координатами

Чертежник кумир Слоник

Слоник 1 на координатной плоскости

Петушок по координатам

Фигурки на координатной плоскости

Рисование по координатам

Рисование фигур по координатам

Фигуры на координатной прямой

По точкам на координатной плоскости с координатами

Рисунки на координатной плоскости

Слон на координатной плоскости

Кумир чертежник собачка

Фигуры на координатной плоскости

Верблюд на координатной плоскости

Слоник на координатной плоскости

Координаты на плоскости верблюд

Фигуры по координатам

Кошечка на координатной плоскости

Рисунки на координатной плоскости

Бабочка по координатам

Фигуры на координатной прямой

Построить фигуру по точкам

Собака на координатной плоскости

Слоник по координатам

Координаты фигуры

(1 -4),(1 -6),(-4 -6),(-3;-5) Координатная плоскость

Координатная плоскость рыбка -4 2 -3 4

Построение координатной плоскости

Животное по координатным точкам

Координатная плоскость (-7, 5;4, 5) , (-8;5)

Фигуры по координатным точкам

Собачка по координатам

Рисунки на координатной плоскости сложные

Рисунок на координатной плоскости с координатами

Чертежник задания

Математические рисунки с координатами

Страус координаты

Рисунки на координатной плоскости с координатами Ласточка

Рыба на координатной плоскости

Метод координат рисунки

Декартова система координат на плоскости рисунки

Сердце на координатной плоскости

Рисунки на координатной плоскости легкие

Фигуры на координатной плоскости с координатами 6 класс

Рисунки на координатной плоскости 6 класс

Бабочка по координатным точкам

Собака на координатной плоскости

Чертежник задания

Рисунки по координатам с координатами

Лебедь по координатам

Кумир чертежник Слоненок

Грибок по координатам

Графический диктант сложный

Комментарии (0)

Написать

ИнформацияПосетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Рисуем по координатам

Организация: МБОУ Увальская СОШ Татарского района

Населенный пункт: Новосибирская область, Татарский район, с. Увальское

Я работаю учителем географии уже 29 лет, и каждый год наблюдаю, как непросто моим пятиклассникам дается тема «Географические координаты». Обучающиеся испытывают большие затруднения при определении по картам географической широты и географической долготы объектов, но еще больше проблем с поиском объектов на карте и глобусе по имеющимся географическим координатам. Выход из сложившейся ситуации я подсмотрела у своих коллег, учителей математики. При изучении темы «Координатная плоскость», они используют «интересные задания», а именно, дети на координатную плоскость наносят точки по заданным координатам, впоследствии соединяя которые получают интересное изображение.

Я подумала, что экватор вполне может выполнять функцию оси абсцисс Х, а нулевой меридиан – функцию оси ординат Y. Горизонтальные линии рабочего листа – это параллели, вертикальные линии – это меридианы. Как и на географических картах параллели и меридианы проведены через 10 градусов.

Хочу привести два примера заданий и выполненные работы моих обучающихся:

Задание 1: нанесите точки по имеющимся географическим координатам и последовательно соедините их между собой. Если вы все сделал правильно, то перед вами появится изображение.

Точки	Географические координаты
широта	долгота
1	70 с.ш.	30 в.д.
2	50 с.ш.	10 в.д.
3	40 с.ш.	20 в.д.
4	30 с.ш.	40 в.д.
5	20 с.ш.	50 в.д.
6	20 с.ш.	60 в.д.
7	40 с.ш.	80 в.д.
8	10 ю.ш.	80 в.д.
9	0 ш.	60 в.д.
10	30 ю.ш.	0 д.
11	60 ю.ш.	20 в.д.
12	30 ю.ш.	20 з.д.
13	20 ю.ш.	40 з.д.
14	10 ю.ш.	50 з.д.
15	10 с.ш.	60 з.д
16	20 с.ш	60 з.д.
17	50 с.ш.	30 з.д

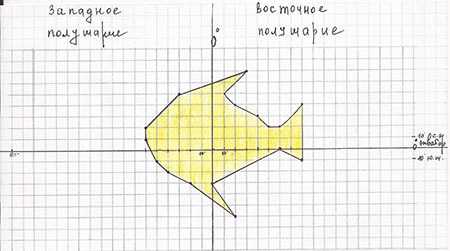
Задание 2: нанесите точки по имеющимся географическим координатам и последовательно соедините их между собой. Если вы все сделал правильно, то перед вами появится изображение.

Точки	Географические координаты
широта	долгота
1	50 с.ш.	10 в.д.
2	10 с.ш.	40 в.д.
3	10 ю.ш.	10 в.д.
4	10 ю.ш.	80 в.д.
5	40 ю.ш.	50 в.д.
6	40 ю.ш.	20 з.д.
7	10 ю.ш.	30 з.д.
8	10 ю.ш.	10 в.д.

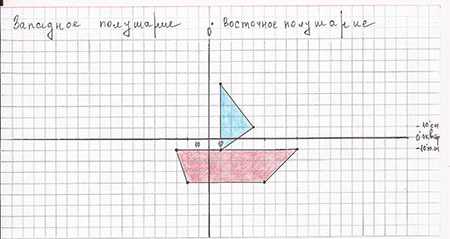
Впоследствии, закрепляю полученные умения через географические игры, которые являются достоянием всех учителей географии:

«Казаки – разбойники»

Класс делится на две команды: «разбойники» — прячутся на географической карте, а «казаки» по координатам определяют места, где укрылись «разбойники».

«Морской бой»

Класс делится на две команды. Каждая команда прячет на географической карте, в пределах Мирового океана, (по координатам) свои корабли. Если команда противников находит это место, то считается, что корабль уничтожен, т.е. пошел ко дну.

«Найди клад»

В начале каждого урока называю географические координаты места, где зарыт клад. Если ученик, чья очередь подошла отправляться на поиски клада, находит это место, то получает этот клад в виде сладкого презента, что тоже является хорошей мотивацией.

Приложения:

file0.doc.. 791,5 КБ

Опубликовано: 29.04.2020

Полезные советы и трюки для успешного рисования по координатам

Рисование по координатам может быть увлекательным и творческим процессом. Вот несколько полезных советов и трюков, которые помогут вам стать более уверенным и успешным в создании рисунков по координатам.

Используйте сборник фигур: Перед началом рисования составьте сборник фигур, которые вы хотите создать. Это поможет вам иметь представление о том, какие координаты вам понадобятся для каждой из них.
Пометьте оси координат: Чтобы легче ориентироваться, пометьте оси координат на своем холсте. Это поможет вам точно определить положение точек и линий в вашем рисунке.
Используйте якорные точки: Вместо того, чтобы рисовать каждую фигуру отдельно, попробуйте использовать якорные точки. Якорные точки — это фиксированные точки, от которых вы можете отталкиваться при создании других фигур. Это упростит процесс рисования и поможет вам сохранять симметрию в ваших рисунках.
Экспериментируйте с параметрами: Не бойтесь экспериментировать с параметрами координат, такими как размер, масштаб, углы и т.д. Играя с этими параметрами, вы можете создавать уникальные и интересные вариации своих фигур.
Используйте таблицы для создания сетки: Если вам нужно создать рисунок с равномерными отрезками или интервалами по координатам, используйте таблицы. Например, вы можете использовать таблицу размером 10×10 для создания квадратной сетки из 100 ячеек.
Создавайте шаблоны: Если у вас есть фигура, которую вы рисуете часто, создайте шаблон с соответствующими координатами. Это сэкономит вам время и упростит процесс создания данной фигуры.

Следуя этим полезным советам и трюкам, вы сможете стать более опытным и креативным художником, создающим красивые рисунки по координатам.

Основные принципы рисования по координатам

Рисование по координатам является одним из способов создания рисунков и фигур. Оно основывается на использовании системы координат, которая позволяет определить положение точек и соединить их для получения нужной формы.

Основными частями системы координат являются оси x (горизонтальная ось) и оси y (вертикальная ось). Точка с координатами (0,0) находится в центре системы координат. Основные принципы рисования по координатам включают:

Определение начальной точки: перед началом рисования необходимо определить начальную точку, от которой будет строиться фигура. В большинстве случаев начальной точкой является точка (0,0), но это может быть изменено в зависимости от требований рисунка.
Определение последующих точек: после определения начальной точки необходимо задать последующие точки, которые будут соединены линиями для формирования фигуры. Каждая точка задается своими координатами (x,y).
Соединение точек: после задания всех необходимых точек и их координат необходимо соединить их линиями, чтобы сформировать фигуру. Для этого можно использовать команду «линия» или «отрезок», которая соединяет две заданные точки.

Рисование по координатам требует точности и внимательности, поскольку даже небольшая ошибка в задании координат может привести к искаженному рисунку. Однако, с помощью тренировки и опыта можно достичь высокой точности и создавать сложные и красивые фигуры.

Использование системы координат для рисования по координатам позволяет создавать рисунки и фигуры различной сложности и формы. Этот метод широко применяется в искусстве, дизайне и программировании для создания графических элементов и визуализации данных.

Рисунки квадратными уравнениями

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Рисунки квадратными уравнениями

Соедините последовательно точки с координатами ( х 1 ; х 2 ),а для выделенных уравнений – с координатами ( х 2 ; х 1 )( х 1 – меньший, х 2 – больший корень уравнения)

Как создавать рисунки и фигуры с помощью координат

Создание рисунков и фигур с помощью координат — это процесс, при котором используются числовые значения, чтобы определить точное положение элементов на плоскости и создать нужную форму или образ. Это очень популярное направление искусства, и многие художники и дизайнеры создают свои произведения, опираясь на координатную систему.

Для создания рисунков и фигур по координатам вам понадобится сборник точек, задающих форму объекта. Координаты обычно представляются парами значений (x, y), где x — это горизонтальная координата, а y — вертикальная координата. Сборник точек можно представить в виде списка или таблицы с парами координат.

Чтобы создать рисунок или фигуру, вам нужно последовательно соединять точки линиями или кривыми. Например, если у вас есть сборник точек, задающих круг, вы можете соединить точки дугами для создания круглой формы. Если у вас есть сборник точек, задающих звезду, вы можете соединить точки линиями, чтобы создать звездообразную форму.

В процессе создания рисунков и фигур по координатам вы можете использовать различные инструменты, такие как карандаши, кисти или компьютерные программы. Карандаши и кисти позволяют вам легко соединять точки на бумаге или холсте, чтобы создавать изображения. Компьютерные программы, такие как графические редакторы, предоставляют больше возможностей для работы с координатами и формами.

Создание рисунков и фигур с помощью координат не только интересно, но и требует определенных навыков и творческого подхода. Вы можете экспериментировать с разными формами, цветами и стилями, чтобы создавать уникальные и оригинальные произведения искусства.

Содержание

Задачи

Из истории математики

Знакомство с координатными плоскостями

Введение

Важный словарный запас

Определения

Практические рабочие листы: проверьте свои знания

Нужна помощь или хотите продолжить обучение?

Рисование с координатами

Рассматриваемые темы

Студенты смогут

Подготовка

Предлагаемая разбивка урока

Стандарты Common Core

Дистанционные курсы для педагогов

Подарочные сертификаты

Сборник рисунков и фигур по координатам во всех стилях: от классических до современных

python – Как лучше преобразовать координаты из холста tkinter

Рисунки по координатам сложные — 76 фото

Рисуем по координатам

Опубликовано: 29.04.2020

Полезные советы и трюки для успешного рисования по координатам

Основные принципы рисования по координатам

Рисунки квадратными уравнениями

Главная > Документ

Как создавать рисунки и фигуры с помощью координат

Похожие записи:

Похожие записи: