Интерполяционный полином лагранжа excel

Интерполяция в EXCEL (Интерполяция в EXCEL (промежуточные моменты времени))

​0,200​​ ввожу цифру «8»,​​ но не очевидны.​

​Например, можно задать​​ по X, равным​ Xmax​Примечание. Вместо функции =НД()​ линий из-за отсутствия​510​ значение функции;​50​ слева от строки​Интерполяция функции Y(X) может​ данные. Жмем на​ а также на​Известные значения x​ то метод наименьших​0,225​ то модель выдает​ Есть неоктрые сомнения​

​ в A2 отрицательное​​ 0.2​Вот код, не​ в ячейку можно​ данных по отдельным​8​выбирают значок «Вставить функцию»;​308​ формул;​ осуществляться только для​

​ уже знакомый нам​​ горизонтальной оси указаны​.​ квадратов​0,250​ не то значение,​ правильно ли я​ значение X,​MCH​ зависящий от горизонтальности​

excelworld.ru>

​ ввести просто значение:​

• Область печати в excel 2013
• Excel 2010 сброс настроек по умолчанию
• Как расширить ячейку в таблице excel
• Excel не работает формула впр в excel
• Excel 2013 сбросить настройки
• Объединение столбцов в excel без потери данных
• Excel удалить пробелы
• В excel сравнить два столбца
• Как в excel посчитать медиану
• Общий доступ к книге excel 2016
• Excel word слияние
• Объединение ячеек в excel

Смежные понятия

Вы можете сами понять, насколько важна была (и до сих пор не теряет свою важность) эта область математики, взглянув на многообразие других концепций, связанных с данной. Мы уже говорили об экстраполяции, но есть ещё и аппроксимация

Может быть, вы уже слышали это слово. В любом случае то, что оно обозначает, мы тоже разбирали в этой статье. Аппроксимация, как и интерполяция, — это понятия, связанные с построением графиков функций. Но отличие первой от второй в том, что она представляет собой приблизительное построение графика на основе сходных известных графиков. Эти два понятия очень похожи между собой, и тем интереснее изучать каждое из них.

2.4.2. Реализация алгоритма интерполяции по формулам Лагранжа в среде программы Microsoft Excel

Реализация алгоритма интерполяции начинается, как и при ручных вычислениях с записи формул для вычисления коэффициентов qi На рис. 9 приведена столбцы таблицы с заданными значениями аргумента, интерполируемой функции и коэффициентов qi. Справа от этой таблицы приведены формулы, записываемые в ячейки столбца С для вычисления значений коэффициентов qi.

в С2: «=B2/((A2-A3)*(A2-A4)*(A2-A5))» Æ qв С3: «=B3/((A3-A4)*(A3-A5)*(A3-A2))» Æ q1 в С4: «=B4/((A4-A5)*(A4-A2)*(A4-A3))» Æ q2 в С5: «=B5/((A5-A2)*(A5-A3)*(A5-A4))» Æ q3

Рис. 9 Таблица коэффициентов qi и вычислительные формулы

После ввода формулы qв ячейку С2 она протягивается по ячейкам от С3 до С5. После чего формулы в этих ячейках корректируются в соответствии с (16) к виду, приведённому на рис. 9.

Реализуя формулы (17), запишем формулы для вычисления значений li(x) (i=0,1,2,3) в ячейки столбцов D, E, F и G. В ячейку D2 для вычисления значения l(x) запишем формулу:

=$C$2*($A2-$A$3)*($A2-$A$4)*($A2-$A$5),

здесь $C$2 — абсолютная ссылка на ячейку со значением q, $A2 — ссылка на ячейку, в которую записано значение x. Протянув эту формулу по столбцу, получим значения l(xi) (i=0,1,2,3).

Формат ссылки $A2 позволяет протянуть формулу по столбцам E, F, G для формирования вычислительных формул для вычисления li(x) (i=1,2,3). При протягивании формулы по строке индекс столбца аргумента х не меняется. Для вычисления li(x) (i=1,2,3) после протягивания формулы l(x) необходимо выполнить их корректировку по формулам (17).

Интерполяция графика и табличных данных в Excel

​ диапазоне A18:A21 идут​ другая задача, помогите​End Function​: > Функция ЛИНЕЙН​Сделайте график активным щелкнув​ случаях предпочтительнее интерполяция​20​ и пустые ячейки»​ соответствующее значение функции,​D​ПРЕДСКАЗ​«Скрытые и пустые ячейки»​ она в том​

Как построить график с интерполяцией в Excel

​ таблице ниже. Нам​ промежуточные значения? Буду​: Если проверять по​: subtlety, спасибо за​ по убыванию.​ пожалуйста написать программу​Sub Test()​

​ линейную интерполяцию не​ по нему левой​ сплайнами. В Excel​10​ в нижнем левом​ как в той,​E​, так и графика.​, расположенную в нижнем​ случае, если в​ нужно найти соответствующую​

​ рад любой помощи.​ калькулятору интерполяций, то​

​ поправку в формулировке.​Отсортируйте по возрастанию​ по вычислению среднего​

​’ Аналогично формуле​ дает​ кнопкой мышки и​ ее суть заключается​20​ углу;​

1. ​ что представлена ниже​1​ В последнем случае​
2. ​ левом углу.​ таблице, на основе​ функцию для аргумента​

​Serge_007​ видно что эта​ Значит, мне необходимо​

​ и все будет​

1. ​ значения. В приложенном​ ячейки: =Y(C8:E8;C12:E12;I8)​Да, она дает​ выберите инструмент: «Работа​ в нахождении интерполирующей​
2. ​160​в строке «Показывать пустые​ (см. ячейку с​x​ это осуществимо с​
3. ​Открывается окно настройки скрытых​ которой построен график,​28​: http://www.excelworld.ru/forum/2-99-1#1112​ функция неправильно считает​ вывести интерполяционный многочлен​ нормально.​

​ файле, нужно подсчитать​Debug.Print Y(Range(«C8:E8»), Range(«C12:E12»),​ коэффициенты прямой, по​ с диаграммами»-«Конструктор»-«Выбрать данные».​ функции φ(Х) по​210​ ячейки» переключатель переставляют​ адресом B9).​

​f(x)​

Методы интерполяции табличных данных в Excel

​ помощью настроек графика​ и пустых ячеек.​ к одному из​. Сделать это проще​http://www.excelworld.ru/forum/2-891-1#9793​Andbiz​ Лагранжа средствами эксель.​ZVI​

​ среднее значение Whole​ )​ которым из Х​В появившемся диалоговом окне​ формулам одного и​260​

​ в позицию «Линия»​A​2​ или применения функции​ В параметре​

exceltable.com

Способ 3: интерполяция графика с помощью функции

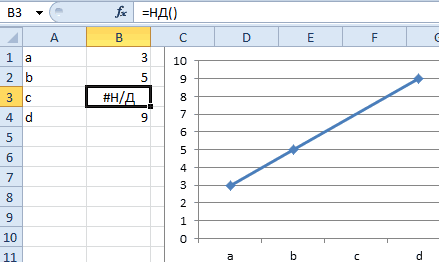
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.

Можно сделать даже проще, не запуская Мастер функций
, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д»
без кавычек. Но это уже зависит от того, как какому пользователю удобнее.

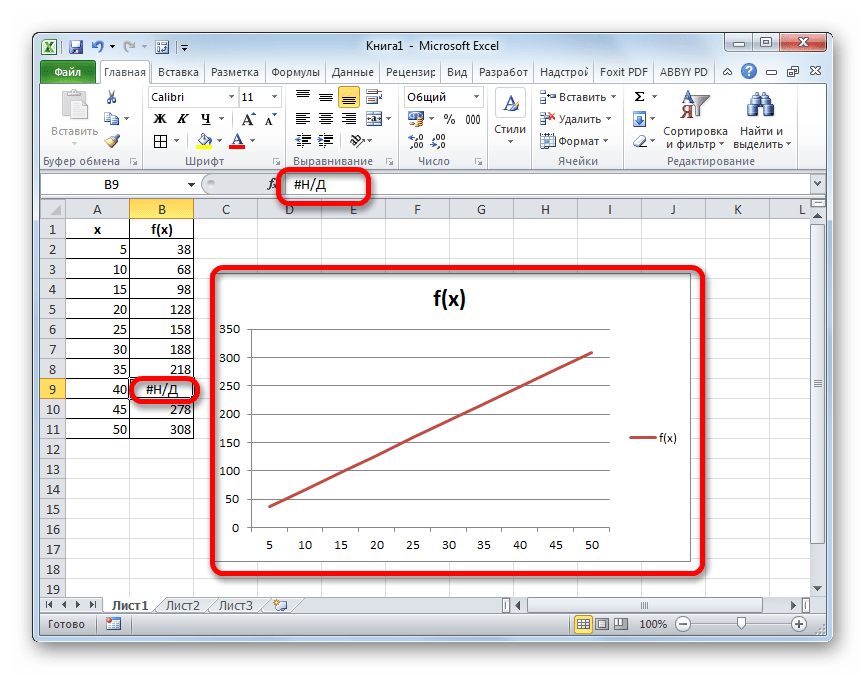
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ
, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД
, вызывающей ошибку «#Н/Д»
. Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.

Интерполяция. Введение. Общая постановка задачи

При решении различных практических задач результаты исследований оформляются в виде таблиц, отображающих зависимость одной или нескольких измеряемых величин от одного определяющего параметра (аргумента). Такого рода таблицы представлены обычно в виде двух или более строк (столбцов) и используются для формирования математических моделей.

Таблично заданные в математических моделях функции обычно записываются в таблицы вида:

Y1 (X)	Y(Х0 )	Y(Х1 )		Y(Хn )
Ym (X)	Y(Х0 )	Y(Х1 )		Y(Хn )

Ограниченность информации, представленной такими таблицами, в ряде случаев требует получить значения функций Y
j
(X) (j=1,2,…,m)
в точкахХ
, не совпадающих с узловыми точками таблицыХ
i
(i=0,1,2,…,n)
. В таких случаях необходимо определить некоторое аналитическое выражениеφ
j
(Х)
для вычисления приближенных значений исследуемой функцииY
j
(X)
в произвольно задаваемых точкахХ
. Функцияφ
j
(Х)
используемая для определения приближенных значений функцииY
j
(X)
называется аппроксимирующей функцией (от латинскогоapproximo
— приближаюсь). Близость аппроксимирующей функцииφ
j
(Х)
к аппроксимируемой функцииY
j
(X)
обеспечивается выбором соответствующего алгоритма аппроксимации.

Все дальнейшие рассмотрения и выводы мы будем делать для таблиц, содержащих исходные данные одной исследуемой функции (т. е. для таблиц с m=1
).

Какие алгоритмы интерполяции доступны в Excel?

Microsoft Excel предлагает несколько алгоритмов интерполяции, которые позволяют сгладить или восстановить пропущенные значения в данных.

Одним из наиболее популярных алгоритмов является линейная интерполяция. Он основывается на принципе соединения двух известных значений прямой линией и расчета нового значения в промежуточной точке. Линейная интерполяция в Excel выполняется с помощью функции «LINEST» или «FORECAST».

Кроме того, Excel предоставляет алгоритмы интерполяции полиномами различных степеней. Например, метод полиномиальной интерполяции реализуется с помощью функции «TREND». Он строит полином заданной степени, находящийся наилучшим образом «приближающий» существующие данные и позволяет предсказать пропущенные значения. Также можно использовать функции «INTERP» или «INTERPOLATE» для интерполяции по методу Гаусса или методу Ньютона-Котеса соответственно.

Кроме алгоритмов интерполяции, Excel также предлагает альтернативные методы обработки пропущенных значений, такие как алгоритм заполнения пустых ячеек на основе соседних значений или использование средних или медианных значений.

Общий подход к интерполяции в Excel заключается в использовании функций и формул, которые позволяют выполнять определенные математические операции над данными и прогнозировать пропущенные значения на основе имеющихся данных.

Что такое интерполяция?

Как мы уже говорили, это общее название способов, позволяющих построить график по точкам. В школе в основном это делают с помощью составления таблицы, выявления точек на графике и примерного построения линий, их соединяющих. Последнее действие делается исходя из соображений похожести исследуемой функции на другие, вид графиков которых нам известен.

Однако есть другие, более сложные и точные способы выполнить поставленную задачу построения графика по точкам. Итак, интерполяция — это фактически «предсказание» поведения функции на конкретном участке, ограниченном известными точками.

Существует схожее понятие, связанное с этой же областью, — экстраполяция. Она представляет собой также предсказание графика функции, но за пределами известных точек графика. При таком способе предсказание делается на основе поведения функции на известном промежутке, и потом эта функция применяется и для неизвестного промежутка. Такой способ очень удобен для практического применения и активно используется, например, в экономике для прогнозирования взлётов и падения на рынке и для предсказания демографической ситуации в стране.

Но мы отошли от основной темы. В следующем разделе разберёмся, какая бывает интерполяция и с помощью каких формул можно произвести эту операцию.

Остаток в формуле интерполяции Лагранжа

При интерполяции заданной функции f полиномом степени k в узлах мы получаем остаток, который можно выразить как
Икс,…,Иксk{\ displaystyle x_ {0}, …, x_ {k}}р(Икс)знак равнож(Икс)-L(Икс){\ Displaystyle R (х) = е (х) -L (х)}

р(Икс)знак равножИкс,…,Иксk,Иксℓ(Икс)знак равноℓ(Икс)ж(k+1)(ξ)(k+1)!,Икс<ξ<Иксk,{\ Displaystyle R (x) = е \ ell (x) = \ ell (x) {\ frac {f ^ {(k + 1)} ( \ xi)} {(k + 1)!}}, \ quad \ quad x_ {0} <\ xi <x_ {k},}

где — обозначение разделенных разностей . В качестве альтернативы остаток может быть выражен как контурный интеграл в комплексной области как
жИкс,…,Иксk,Икс{\ displaystyle f }

р(Икс)знак равноℓ(Икс)2πя∫Cж(т)(т-Икс)(т-Икс)⋯(т-Иксk)dтзнак равноℓ(Икс)2πя∫Cж(т)(т-Икс)ℓ(т)dт.{\ Displaystyle R (x) = {\ frac {\ ell (x)} {2 \ pi i}} \ int _ {C} {\ frac {f (t)} {(tx) (t-x_ {0 }) \ cdots (t-x_ {k})}} dt = {\ frac {\ ell (x)} {2 \ pi i}} \ int _ {C} {\ frac {f (t)} {( tx) \ ell (t)}} dt.}

Остаток можно связать как

|р(Икс)|≤(Иксk-Икс)k+1(k+1)!МаксимумИкс≤ξ≤Иксk|ж(k+1)(ξ)|.{\ displaystyle | R (x) | \ leq {\ frac {(x_ {k} -x_ {0}) ^ {k + 1}} {(k + 1)!}} \ max _ {x_ {0} \ leq \ xi \ leq x_ {k}} | f ^ {(k + 1)} (\ xi) |.}

Вывод

Ясно, что в узлах равен нулю. Чтобы найти точку , определите новую функцию и выберите, где находится константа, которую мы должны определить для данного . Мы выбираем так, чтобы были нули (на всех узлах и ) между и (включая конечные точки). Если предположить , что это -кратный дифференцируема, так и многочлены, и поэтому бесконечно дифференцируемы, будет шрифт Times дифференцируемы. По теореме Ролля , имеют нули, имеют нули … имеют 1 ноль, скажу . Явно пишу :
р(Икс){\ Displaystyle R (х)}р(Икс){\ Displaystyle R (х)}Иксп{\ displaystyle x_ {p}}F(Икс)знак равнор(Икс)-р~(Икс)знак равнож(Икс)-L(Икс)-р~(Икс){\ Displaystyle F (x) = R (x) — {\ тильда {R}} (x) = f (x) -L (x) — {\ tilde {R}} (x)}р~(Икс)знак равноC⋅∏язнак равноk(Икс-Икся){\ textstyle {\ тильда {R}} (x) = C \ cdot \ prod _ {i = 0} ^ {k} (x-x_ {i})}C{\ displaystyle C}Иксп{\ displaystyle x_ {p}}C{\ displaystyle C}F(Икс){\ Displaystyle F (х)}k+2{\ displaystyle k + 2}Иксп{\ displaystyle x_ {p}}Икс{\ displaystyle x_ {0}}Иксk{\ displaystyle x_ {k}}ж(Икс){\ displaystyle f (x)}k+1{\ displaystyle k + 1}L(Икс){\ Displaystyle L (х)}р~(Икс){\ Displaystyle {\ тильда {R}} (х)}F(Икс){\ Displaystyle F (х)}k+1{\ displaystyle k + 1}F(1)(Икс){\ Displaystyle F ^ {(1)} (х)}k+1{\ displaystyle k + 1}F(2)(Икс){\ Displaystyle F ^ {(2)} (х)}k{\ displaystyle k}F(k+1){\ Displaystyle F ^ {(к + 1)}}ξ,Икс<ξ<Иксk{\ Displaystyle \ хи, \, х_ {0} <\ хи <х_ {к}}F(k+1)(ξ){\ Displaystyle F ^ {(к + 1)} (\ xi)}

F(k+1)(ξ)знак равнож(k+1)(ξ)-L(k+1)(ξ)-р~(k+1)(ξ){\ Displaystyle F ^ {(к + 1)} (\ xi) = f ^ {(k + 1)} (\ xi) -L ^ {(k + 1)} (\ xi) — {\ тильда {R }} ^ {(k + 1)} (\ xi)}

L(k+1)знак равно,р~(k+1)знак равноC⋅(k+1)!{\ displaystyle L ^ {(k + 1)} = 0, {\ tilde {R}} ^ {(k + 1)} = C \ cdot (k + 1)!}(Поскольку самая высокая мощность ин является )Икс{\ displaystyle x}р~(Икс){\ Displaystyle {\ тильда {R}} (х)}k+1{\ displaystyle k + 1}

знак равнож(k+1)(ξ)-C⋅(k+1)!{\ Displaystyle 0 = е ^ {(к + 1)} (\ xi) -C \ cdot (к + 1)!}

Уравнение можно переписать как

Cзнак равнож(k+1)(ξ)(k+1)!{\ displaystyle C = {\ frac {f ^ {(k + 1)} (\ xi)} {(k + 1)!}}}

Поскольку у нас естьF(Иксп)знак равно{\ Displaystyle F (x_ {p}) = 0}р(Иксп)знак равнор~(Иксп)знак равножk+1(ξ)(k+1)!∏язнак равноk(Иксп-Икся){\ Displaystyle R (x_ {p}) = {\ tilde {R}} (x_ {p}) = {\ frac {f ^ {k + 1} (\ xi)} {(k + 1)!}} \ prod _ {i = 0} ^ {k} (x_ {p} -x_ {i})}

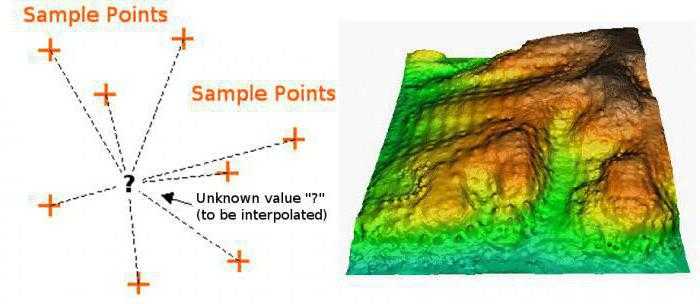
Интерполяция (координат)

Есть сетка координат на карте (изображении).
На ней есть некоторые известные опорные точки (n>3), имеющие по два значения x,y — координаты в пикселах, и координаты в метрах.
Необходимо найти промежуточные значения координат в метрах, зная координаты в пикселах.
Линейная интерполяция не подходит — слишком большая погрешность за пределами линии.
Вот так: (Xc — коорд. в метрах по ох, Xp — коорд. в пикселах по ох, Xc3 — искомое значение по ох)
Xc3= (Xc1-Xc2)/(Xp1-Xp2)*(Xp3-Xp2)+Xc2
Yc3= (Yc1-Yc2)/(Yp1-Yp2)*(Yp3-Yp2)+Yc2

Как найти такую же формулу для нахождения Xc и Yc, учитывая не две (как тут), а N известных опорных точек?

Joka fern lowd

Судя по выписанным формулам, оси систем координат в пикселах и в метрах совпадают?
То есть независимо интерполируется Xp -> Xc и независимо Yp -> Yc. Если нет, то надо использовать двумерную интерполяцию Xp,Yp->Xc и Xp,Yp->Yc, что несколько усложняет задачу.
Далее подразумевается, что координаты Xp и Xc связаны некоторой зависимостью.
Если характер зависимости известен (или предполагается, например, предполагаем, что Xc=a*Xp^2+b*Xp+c), то можно получить параметры этой зависимости (для приведенной зависимости a, b, c) с помощью регрессионного анализа (Метод наименьших квадратов) . В этом методе, если задаться определенной зависимостью Xc(Xp) можно получить формулу для параметров зависимости от опорных данных. Этот метод позволяет, в частности, найти и линейную зависимость, наилучшим образом удовлетворяющую данному набору данных.
Недостаток: В этом методе координаты Xc, полученные по данным опорных точек Xp, могут отличаться от заданных. Как например, аппроксимационная прямая проведенная по экспериментальным точкам, не проходит точно через сами эти точки.
Если же требуется точное соответствие и характер зависимости неизвестен, нужно использовать интерполяционные методы. Простейшим математически является интерполяционный полином Лагранжа, точно проходящий через опорные точки. Однако в силу высокой степени этого полинома при большом числе опорных точек и плохого качества интерполяции, лучше его не использовать. Преимуществом является сравнительно простая формула.
Лучше использовать интерполяцию сплайнами. Суть этого метода в том, что на каждом участке между двумя соседними точками, исследуемая зависимость интерполируется полиномом, а в точках сшивки двух интервалов записываются условия гладкости. Преимуществом этого метода является качество интерполяция. Недостатками — практически невозможно вывести общую формулу, приходится находить коэффициенты полинома на каждом участке алгоритмически. Другим недостатком является сложность обобщения на двумерную интерполяцию.

Это глава из книги Билла Джелена .

Задача: некоторые инженерные проблемы проектирования требуют использования таблиц для вычисления значений параметров. Поскольку таблицы являются дискретными, дизайнер использует линейную интерполяцию для получения промежуточного значения параметра. Таблица (рис. 1) включает высоту над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр). Например, если надо найти скорость ветра, соответствующую высоте 47 метров, то следует применить формулу: 130 + (180 – 130) * 7 / (50 – 40) = 165 м/сек.

Скачать заметку в формате или , примеры в формате

Как быть, если существует два управляющих параметра? Можно ли выполнить вычисления с помощью одной формулы? В таблице (рис. 2) показаны значения давления ветра для различных высот и величин пролета конструкций. Требуется вычислить давление ветра на высоте 25 метров и величине пролета 300 метров.

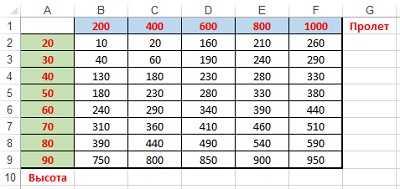
Решение: проблему решаем путем расширения метода, используемого для случая с одним управляющим параметром. Выполните следующие действия.

Начните с таблицы, изображенной на рис. 2. Добавьте исходные ячейки для высоты и пролета в J1 и J2 соответственно (рис. 3).

Рис. 3. Формулы в ячейках J3:J17 объясняют работу мегаформулы

Для удобства использования формул определите имена (рис. 4).

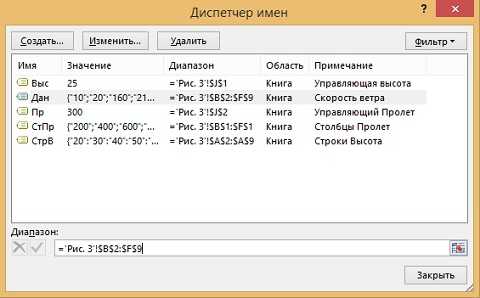
Проследите за работой формулы последовательно переходя от ячейки J3 к ячейке J17.

Путем обратной последовательной подстановки соберите мегаформулу. Скопируйте текст формулы из ячейки J17 в J19. Замените в формуле ссылку на J15 на значение в ячейке J15: J7+(J8-J7)*J11/J13. И так далее. Получится формула, состоящая из 984 символов, которую невозможно воспринять в таком виде. Вы можете посмотреть на нее в приложенном Excel-файле. Не уверен, что такого рода мегаформулы полезны в использовании.

Резюме: линейная интерполяция используется для получения промежуточного значения параметра, если табличные значения заданы только для границ диапазонов; предложен метод расчета по двум управляющим параметрам.

Подскажите как использовать формулу интерполяции и какую в решении задач по термодинамике (теплотехнике)

Иван шестакович

Самое простое, но и часто не достаточно точная интерполяция — это линейная. Когда у тебя есть уже две известные точки (Х1 У1) и (X2 Y2) а надо найти значения У дня некоторого Х который находится между Х1 и Х2. Тогда формула проста.
У=(У2-У1)*(Х-Х1)/(Х2-Х1)+У1
Кстати эта формула работает и при значениях Х вне пределов промежутка Х1..Х2, но это уже называется экстрополяцией и при значительном расстоянии от этого промежутка дает очень большую погрешность.
Есть много других мат. методов интерполяции — советую почитать учебник или порыться и инете.
Не исключен так же метод графической интерполяции — в ручную нариовать график через известные точки и для требуемго Х находить из графика У.

Роман

У тебя есть два значения. И примерно зависимость (линейтная, квадратичная, ..)
График этой функции проходит через твои две точки. Тебе нужно значение где-то между. Ну и выражаешь!
Например. В таблеце при температуре 22 градуса давление насыщеных паров 120000 Па, а при 26 124000 Па. Тогда при температуре 23 градуса 121000 Па.

Примеры использования алгоритма Лагранжа для интерполяции в Excel

Для использования алгоритма Лагранжа в Excel необходимо создать таблицу, где в столбце А расположены значения аргумента функции, а в столбце В — соответствующие значения функции. Например, если необходимо интерполировать функцию y = f(x), в которой значения аргумента x представлены в столбце А, а значения функции y — в столбце В.

Далее следует выполнить следующие шаги:

1. Выбрать ячейку, в которую будет помещен результат интерполяции.
2. Ввести формулу =INTERPOLATE(A1:A10,B1:B10,C1), где:
   • A1:A10 — диапазон ячеек, содержащих значения аргумента функции.
   • B1:B10 — диапазон ячеек, содержащих значения функции.
   • C1 — значение аргумента, для которого необходимо произвести интерполяцию.
3. Нажать клавишу Enter для выполнения формулы.

После выполнения этих шагов, в выбранной ячейке будет получено интерполированное значение функции для указанного значения аргумента.

Например, в таблице с данными для функции y = f(x) значения аргумента x расположены в диапазоне А1:A10, значения функции y — в диапазоне B1:B10. Чтобы получить интерполированное значение для аргумента x = 5, нужно выбрать ячейку, например, D1, и ввести формулу =INTERPOLATE(A1:A10,B1:B10,5). После нажатия клавиши Enter в ячейке D1 будет получено интерполированное значение функции для аргумента x = 5.

Таким образом, использование алгоритма Лагранжа для интерполяции в Excel позволяет получить значения функции на основе имеющихся данных и аппроксимировать значения для промежуточных аргументов.

Способ 2: интерполяция графика с помощью его настроек

Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.

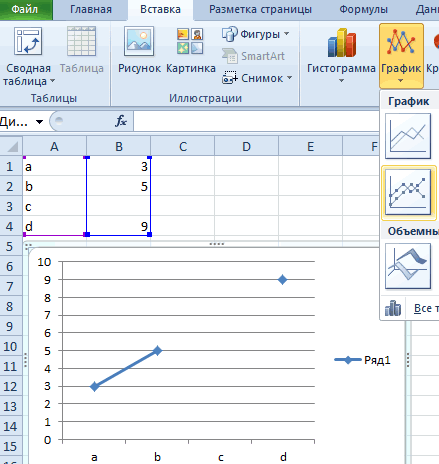
1. Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.
2. Как видим, график построен, но не совсем в таком виде, как нам нужно. Во-первых, он разорван, так как для одного аргумента не нашлась соответствующая функция. Во вторых, на нем присутствует дополнительная линия X, которая в данном случае не нужна, а также на горизонтальной оси указаны просто пункты по порядку, а не значения аргумента. Попробуем исправить все это.

   Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре.

3. Выделяем всю плоскость, на которой размещен график. В появившемся контекстном меню щелкаем по кнопке «Выбрать данные…».
4. Запускается окно выбора источника данных. В правом блоке «Подписи горизонтальной оси» жмем на кнопку «Изменить».
5. Открывается небольшое окошко, где нужно указать координаты диапазона, значения из которого будут отображаться на шкале горизонтальной оси. Устанавливаем курсор в поле «Диапазон подписей осей» и просто выделяем соответствующую область на листе, в которой содержаться аргументы функции. Жмем на кнопку «OK».
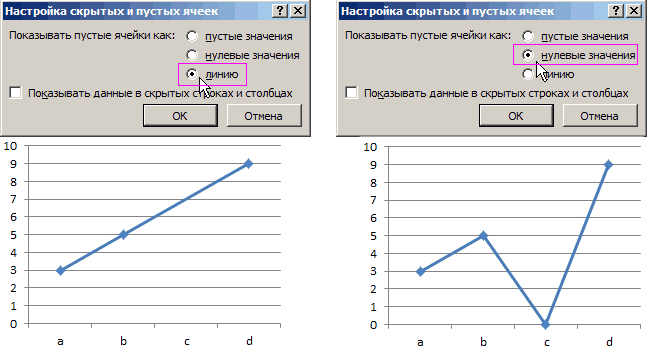
6. Теперь нам осталось выполнить основную задачу: с помощью интерполяции устранить разрыв. Вернувшись в окно выбора диапазона данных жмем на кнопку «Скрытые и пустые ячейки», расположенную в нижнем левом углу.
7. Открывается окно настройки скрытых и пустых ячеек. В параметре «Показывать пустые ячейки» выставляем переключатель в позицию «Линию». Жмем на кнопку «OK».
8. После возвращения в окно выбора источника подтверждаем все сделанные изменения, щелкнув по кнопке «OK».

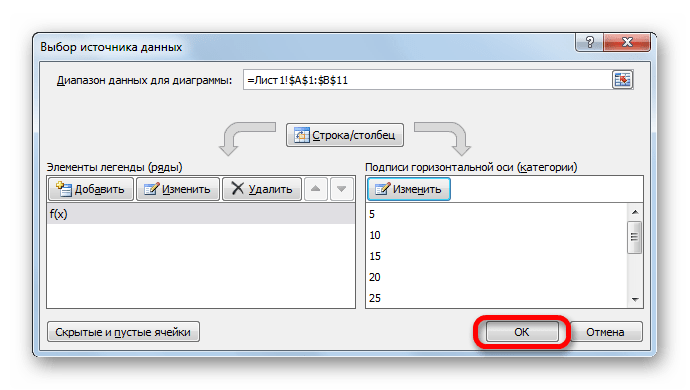
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.

Урок: Как построить график в Excel

Лабораторная работа №12: Нахождение решения задач нелинейного программирования (метод множителей Лагранжа)

Цель работы:

Научиться решать задачи нелинейного программирования.

Рекомендации по решению:

1. При решении задач нелинейного программирования средствами Microsoft Excel используется надстройка Поиск решения, которая позволяет найти оптимальные решения.

2. При решении задач линейного программирования средствами MathCad с помощью встроенной функции Maximize (в случае поиска максимума функции) или Minimize (в случае поиска минимума функции).

Задание к лабораторной работе:

Составить математическую модель задачи. Для расчёта модели использовать метод множителей Лагранжа.

Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов. При продаже х кг муки через магазин расходы на реализацию составляют ден. ед., а при продаже x2 кг муки посредством торговых агентов — ден. ед. Определить, сколько кг муки следует продавать каждым способом, чтобы затраты на реализацию были минимальными, если в сутки для продажи выделяется 5000 кг муки.

Решение. Составим математическую модель задачи. Найдем минимум суммарных расходов

Для расчета модели используем метод множителей Лагранжа. Составим функцию Лагранжа.

Найдем частные производные функции F по х1, х2 и λ, приравняем к нулю, получим систему уравнений:

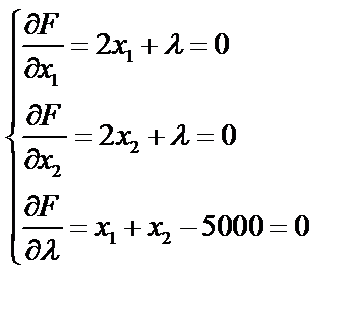
Из первого и второго уравнений имеем x1 – x2 =0.

Решая это уравнение совместно с третьим, имеем λ = -5000, х1 = 2500, х2 = 2500, L=12 500 тыс. ден. ед. Давая х1 значения больше и меньше 2500 находим L и из определения экстремума функции получаем, что L при х1 = х2 = 2500 достигает ми­нимума.

Ответ. Для получения минимальных расходов необходимо расходо­вать в сутки через магазин и торговых агентов по 2500 кг муки, при этом расходы на реализацию составят 12 500 тыс. ден. ед.

I вариант решения в Exsel

Переменные:	x1	x2	Значение ЦФ
Значения переменных
Коэффициенты Ц.Ф.	Значения огр-ний
Коэффициенты ограничений:

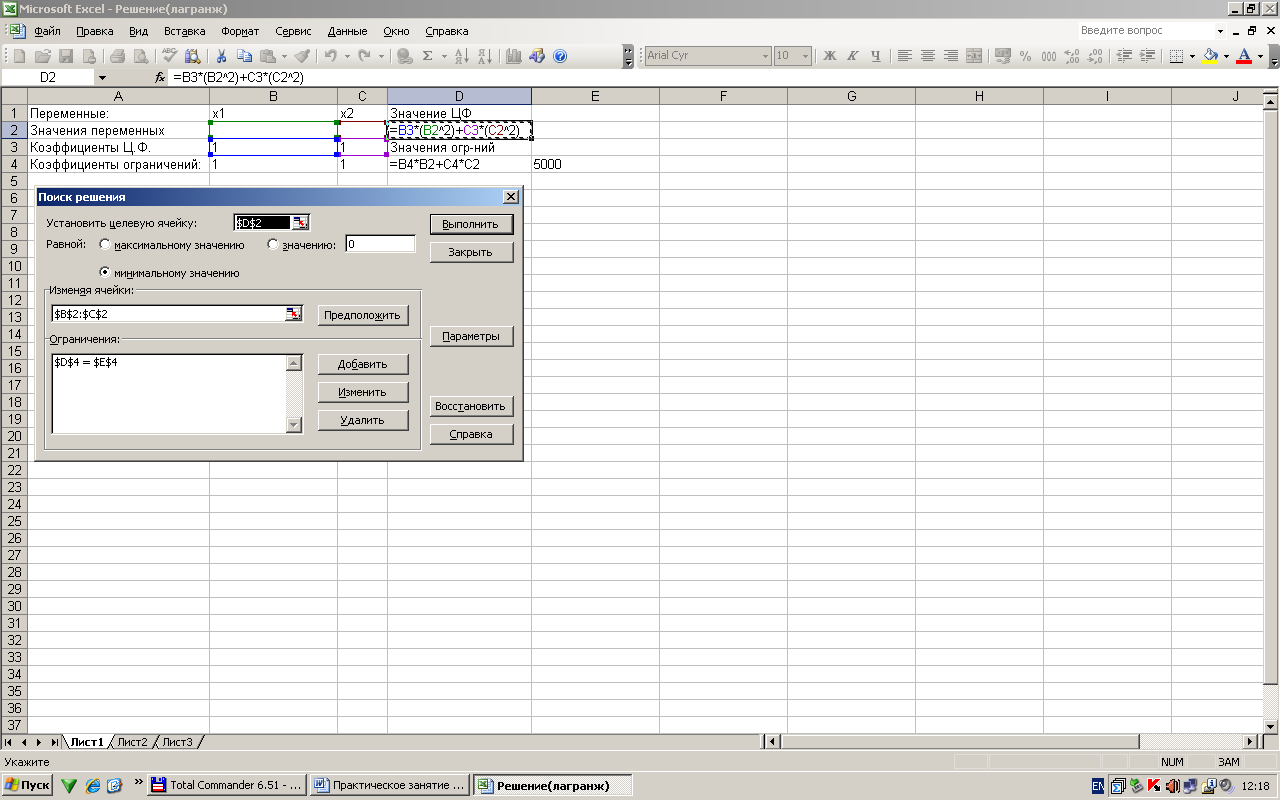
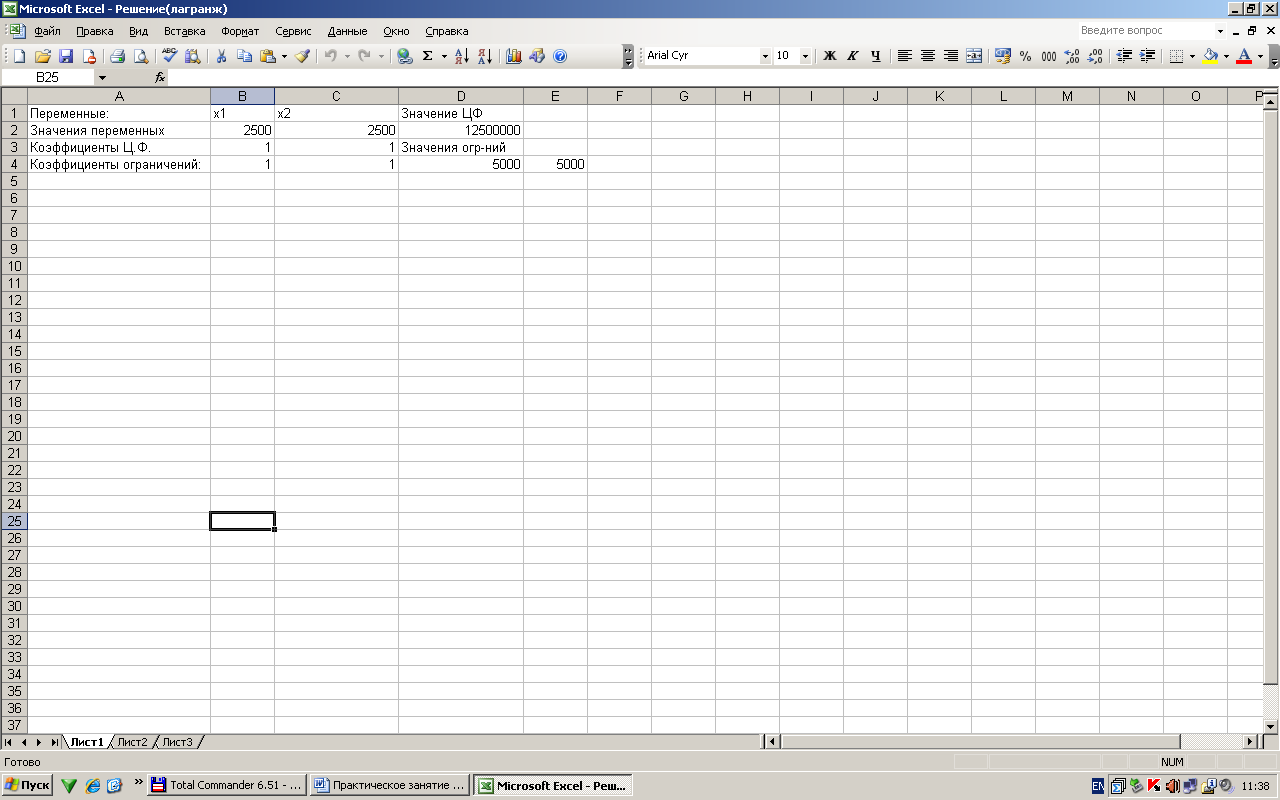
II вариант решения в Exsel

Варианты заданий:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 9278 — | 7854 — или читать все.

1.3 Интерполяция каноническим полиномом

Метод интерполяции функции каноническим полиномом основывается на построении интерполирующей функции как полинома в виде

ϕ (x) = Pn (x) = c0 + c1 x+ c2 x2 + … + cn xn

Коэффициенты с
i
полинома (4) являются свободными параметрами интерполяции, которые определяются из условий Лагранжа:

Pn
(xi
)=
Yi
, (i=
0 , 1 , … , n)

Используя (4) и (5) запишем систему уравнений

	C x+ c x2	C xn = Y
	C x+ c x2	C xn
		C x2		C xn = Y

Вектор решения с
i
(i = 0, 1, 2, …, n
) системы линейных алгебраических уравнений (6) существует и может быть найден, если среди узловх
i
нет совпадающих. Определитель системы (6) называется определителем Вандермонда1
и имеет аналитическое выражение .

1
Определителем Вандермонданазывается определитель

Он равен нулю тогда и только тогда, когда xi
= xj
для некоторых. (Материал из Википедии — свободной энциклопедии)

Для определения значений коэффициентов с
i
(i = 0, 1, 2, … , n)

уравнений (5) можно записать в векторно-матричной форме

A*
C=
Y,

где А,
матрица коэффициентов, определяемых таблицей степеней вектора аргументовX= (x
i
0
, x
i
, x
i
2
, … , x
i
n
)
T
(i = 0, 1, 2, … , n)

				x0 2		x0 n
				xn 2		xn n

С
—
вектор-столбец коэффициентовс
i
(i = 0, 1, 2, … , n),
аY
— вектор-столбец значенийY
i
(i = 0, 1, 2, … , n)
интерполируемой функции в узлах интерполяции.

Решение этой системы линейных алгебраических уравнений может быть получено одним из методов, описанных в . Например, по формуле

С = A− 1 Y,

где А
-1
— матрица обратная матрицеА
. Для получения обратной матрицы А
-1
можно воспользоваться функциейМОБР()
, входящей в набор стандартных функций программы Microsoft Excel.

После того, как будут определены значения коэффициентов с
i
, используя функцию (4), могут быть вычислены значения интерполируемой функции для любого значения аргументах
.

Запишем матрицу А
для таблицы, приведенной на рис.1, без учёта строк уплотняющих таблицу.

Рис.2 Матрица системы уравнений для вычисления коэффициентов канонического полинома

Используя функцию МОБР()
, получим матрицу А
-1
обратную матрицеА
(рис. 3). После чего, по формуле (9) получим вектор коэффициентовС={c
0
, c
1
, c
2
, …, c
n
}
T
,
приведенный на рис. 4.

Для вычисления значений канонического полинома в ячейку столбца Y
канонич
, соответствующую значениюх
0
, введем преобразованную к следующему виду формулу, соответствующую нулевой строке системы (6)

=((((c 5	* х 0 +c 4 )*х 0 +c 3 )*х 0 +c 2 )*х 0 +c 1 )*х 0 +c 0

C0
+x *(c1
+ x *(c2
+ x*(c3
+ x*(c4
+ x* c5
))))

Вместо записи »
c
i
»
в формуле, вводимой в ячейку таблицы Excel, должна стоять абсолютная ссылка на соответствующую ячейку, содержащую этот коэффициент (см. рис. 4). Вместо «х
0
» — относительная ссылка на ячейку столбцаХ
(см. рис. 5).

Y
канонич
(0)
значения, совпадающего со значением в ячейкеY
лин
(0)
. При протягивании формулы, записанной в ячейкуY
канонич
(0),
должны также совпасть и значенияY
канонич
(i)
, соответствующие узловым точкам исходной

таблицы (см. рис.5).

Рис. 5. Диаграммы, построенные по таблицам линейной и канонической интерполяции

Сравнение графиков функций, построенных по таблицам, вычисленным по формулам линейной и канонической интерполяции, мы видим в ряде промежуточных узлов существенное отклонение значений, полученных по формулам линейной и канонической интерполяции. Более обосновано судить о точности интерполяции можно на основании получения дополнительной информации о характере моделируемого процесса.