Улитка паскаля в excel как сделать

Простейший график изменений

График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.

Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:

Год	Чистая прибыль*
2010	13742
2011	11786
2012	6045
2013	7234
2014	15605

* Цифры условные, для учебных целей.

Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:

Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.

Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:

Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.

Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:

Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».

Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:

Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).

Шаг 1: Создание таблицы данных

Первым шагом для построения графика улитки Паскаля в Excel необходимо создать таблицу данных. В данной таблице будут содержаться числа треугольника Паскаля, которые будут использованы для построения графика.

Для начала, создайте новую книгу в Excel и перейдите на лист, на котором будет располагаться ваша таблица. Затем, введите необходимое количество строк и столбцов для таблицы данных. Желательно выбрать столько строк и столбцов, чтобы было достаточно места для размещения всех чисел треугольника Паскаля, которые вы планируете использовать.

Затем, заполните ячейки таблицы данными чисел треугольника Паскаля. Для этого, следуйте следующему алгоритму:

1. В первом столбце (столбец А) введите число 1 в первую ячейку (ячейка А1).
2. Затем, в каждую следующую ячейку первого столбца введите число 1, увеличивая его на 1 с каждой новой ячейкой.
3. Во втором столбце (столбец В) введите числа треугольника Паскаля. Начните со второй ячейки (ячейка В2).
4. Для заполнения каждой следующей ячейки треугольника Паскаля, сложите числа из ячеек над ней в предыдущем столбце и в ячейке слева от нее в текущем столбце. Введите полученный результат в текущую ячейку.

Повторите шаги 3-4 для каждого следующего столбца таблицы, заполняя таблицу числами треугольника Паскаля до тех пор, пока не будут заполнены все необходимые строки и столбцы.

После того, как таблица данных будет заполнена, вы можете перейти ко второму шагу — созданию графика улитки Паскаля в Excel.

На этом шаге вы создали таблицу данных, которая содержит числа треугольника Паскаля. Теперь вы готовы перейти к следующему шагу — созданию графика улитки Паскаля.

Как нарисовать касательную линию в Excel – Вокруг-Дом – 2021

Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:

Создайте строку на листе в программе, вписав туда известные значения X.

Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.

Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.

Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.

Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.

В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.

Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).

Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.

Шаг 1

Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.

Шаг 2

Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.

Как сделать касательную в excel к графику

Argument ‘Topic id’ is null or empty

Николай Павлов, Planetaexcel, 2006-2021 info@planetaexcel.ru

Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.

За изображения спасибо Depositphotos.com

ИП Павлов Николай Владимирович ИНН 633015842586 ОГРН 310633031600071

Шаг 3

Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.

Шаг 4

Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.

Метод касательной сделать в MS Excel

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Метод касательной, нахождение производнойКак найти производную? У меня программа для решения уравнения методом касательной. На форме.

Метод касательной (Ньютона). Нужно исправить программуProgram kasat; var a,b,x,eps:real;n:integer; function f (x:real):real; begin.

Как сделать вылет шара по касательнойДобрый день! Столкнулся со следующей проблемой. В моем примере два шара А и Б. А — неподвижный.

Excel: Сделать List (of Excel.Range) по столбцу с пустыми и заполненными ячейкамиДоброго времени! За несколько часов так и не решил задачку. Файл Excel в столбце D имеет.

Как сделать в Excel сделать матрицу из коэффициентов и столбца свободных членов (ТММ)В общем мне нужно рассчитать Синтез и кинематику шарнирного четырехзвенного механизма в Excel.

Метод SaveAs в ExcelВсем доброго времени суток.Помогите разобраться с методом SaveAs Есть,ну назовем ее,небольшая.

Метод дихотомии — MS ExcelЗдравствуйте) помогите пожалуйста найти минимум функции f(X) = 2*Х^2 + EXP(-X). Есть пример этого.

Метод Крамера в ExcelДоброго времени суток! Прошу помощи с работой в MS Exel. Низко кланяюсь и извиняюсь за.

Формула Бернулли в Эксель

Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.

Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .

Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).

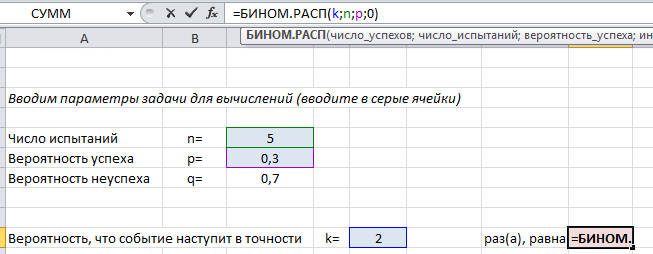
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:

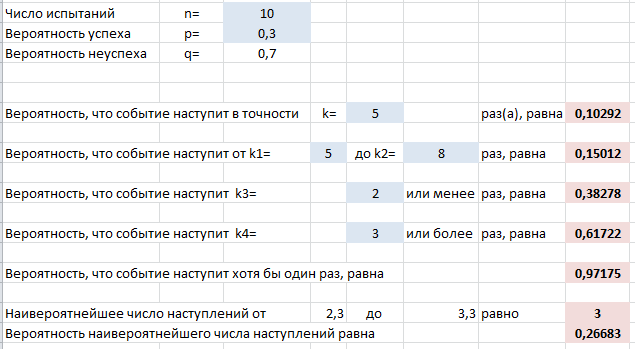
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):

• Событие произойдет в точности $k$ раз из $n$: =БИНОМ.РАСП(k;n;p;0) $$P_n(k)=C_n^k cdot p^k cdot q^$$
• Событие произойдет от $k_1$ до $k_2$ раз: =БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0) $$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$
• Событие произойдет не более $k_3$ раз: =БИНОМ.РАСП(k_3;n;p;1) $$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$
• Событие произойдет не менее $k_4$ раз: =1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0) $$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$
• Событие произойдет хотя бы один раз: =1-БИНОМ.РАСП(0;n;p;0) $$P_n( X ge 1)=1-P_n(0)=1-q^$$
• Наивероятнейшее число наступлений события $m$: =ОКРУГЛВВЕРХ(n*p-q;0) $$np-q le m le np+p$$

Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.

Как построить график улитка Паскаля в Excel

Чтобы построить график улитки Паскаля в Excel, вам потребуется следующая информация:

1. Откройте программу Excel и создайте новый лист. Введите числа треугольника Паскаля в ячейки, начиная с верхнего левого угла. Например, начните с числа 1 в ячейке A1.
2. Для удобства, можно воспользоваться формулой для автоматического заполнения ячеек треугольника Паскаля. Введите в ячейку A1 число 1, затем в ячейку A2 введите формулу «=A1», а в ячейку A3 введите формулу «=A1+A2». Выделите обе ячейки с формулами и перетяните их вниз, чтобы Excel заполнил оставшиеся ячейки треугольника.
3. Теперь нужно построить график на основе полученных чисел. Выберите все ячейки с числами треугольника Паскаля, включая пустые ячейки. Нажмите правую кнопку мыши и выберите «Скопировать».
4. Перейдите на лист, на котором хотите построить график, и нажмите правую кнопку мыши. Выберите «Вставить» и затем «Вставить специально». В появившемся окне выберите «Значения» и нажмите «ОК».
5. Теперь выберите все числа треугольника Паскаля, включая пустые ячейки, и нажмите «Вставить».
6. Выделите полученные числа и нажмите на кнопку «Диаграмма» на вкладке «Вставка». Выберите нужный тип диаграммы и нажмите «ОК».
7. Измените необходимые настройки диаграммы, такие как шрифты, цвета и заголовки.

Теперь у вас есть график улитки Паскаля в Excel. Вы можете изменять числа треугольника и обновлять график вручную, либо использовать формулы Excel для автоматического обновления.

Простой гид для создания спирали Архимеда в программе Excel

Создание графического изображения спирали Архимеда в программе Excel не требует высоких навыков работы в данном ПО. В этой статье мы рассмотрим простой гид для создания данной фигуры.

Шаг 1. Создание таблицы данных

Для начала необходимо создать таблицу данных, которая будет содержать значения координат x и y для нашей спирали Архимеда.

В первой колонке введите значения углов в радианах от 0 до 10π (или любые другие значения, в зависимости от вашего проекта). Для этого можно воспользоваться функцией «PI()» или ввести значения вручную.

Во второй колонке напишите формулу для расчета координат x и y в соответствии с уравнением спирали Архимеда:

Здесь a — коэффициент масштабирования, а θ — угол в радианах.

После ввода формул, заполните таблицу данными, используя автозаполнение.

Шаг 2. Создание диаграммы

Для создания диаграммы спирали Архимеда в Excel необходимо выполнить следующие действия:

Выделите все ячейки таблицы с данными с помощью мыши.

Нажмите на вкладку «Вставка» на главной панели инструментов Excel.

Выберите тип диаграммы «Рассеяние» в разделе «Диаграммы».

Выберите один из предложенных вариантов оформления.

После этого Excel создаст диаграмму спирали Архимеда.

Шаг 3. Оформление диаграммы

Для того чтобы диаграмма выглядела более привлекательно, можно изменить ее внешний вид. Для этого можно использовать следующие элементы:

• Заголовок диаграммы;
• Оси координат;
• Цвет линии и маркеров;
• Масштабирование.

Чтобы изменить параметры графика, выполните следующие действия:

Выберите диаграмму с помощью мыши.

Нажмите на кнопку «Диаграмма» на главной панели инструментов Excel.

В выпадающем меню выберите «Оформление диаграммы».

В появившемся окне выберите вкладку «Оси», чтобы настроить оси координат.

Для изменения цвета линии и маркеров выберите соответствующую вкладку настроек.

Готово! Теперь вы можете наслаждаться своим графиком спирали Архимеда в Excel.

Вывод

Создание спирали Архимеда в программе Excel — это простой и увлекательный процесс, который может быть использован в различных проектах. С помощью шагов, описанных в этой статье, вы сможете создать свой собственный график в несколько минут. Удачи!

Шаг 5: Настройка внешнего вида графика

После того как мы построили график улитка Паскаля с помощью диаграммы рассеяния и добавили подписи осей и заголовок, мы можем приступить к настройке его внешнего вида.

В Excel есть множество инструментов для настройки внешнего вида графиков. Воспользуемся некоторыми из них, чтобы сделать наш график привлекательным и понятным.

• Выберите график, чтобы активировать вкладку «Рисование» на ленте.
• На вкладке «Рисование» вы найдете различные инструменты для изменения цветов, шрифтов, фона и других параметров графика.
• Измените цвет линий и маркеров точек, чтобы легче различать разные диаграммы.
• Добавьте легенду, чтобы обозначить каждую диаграмму улитки Паскаля.
• Измените шрифт и размер подписей осей и заголовка, чтобы сделать их более разборчивыми.
• Настройте размеры графика и его положение на листе, чтобы он лучше вписывался в документ.

Это только некоторые возможности настройки внешнего вида графика улитка Паскаля в Excel. Вы можете экспериментировать с различными возможностями и настройками, чтобы достичь желаемого результата.

После настройки внешнего вида графика можно сохранить его в формате изображения или вставить его в другой документ Excel или в презентацию PowerPoint.

Теперь у вас есть все необходимые навыки, чтобы построить график улитка Паскаля в Excel. Не останавливайтесь на достигнутом — продолжайте экспериментировать и создавать удивительные графики!

Добавление второй оси

Иногда информация может быть представлена в таблице так, что поместить ее на одной общей диаграмме, на первый взгляд, невозможно. Если представить, что накладные расходы указаны не в рублях, а в долларах, график получится некорректным.

Можно построить две разных диаграммы для каждого ряда данных. Или перед тем, как сделать график в Экселе, пересчитать сумму по действующем курсу — но это будет не слишком правильно, если затраты определялись именно в валюте. Решение проблемы — добавить вторую ось со своими единицами измерения. 

Для этого можно выполнить такие действия: 

1. Построить основу — график, единицы измерения у которого одинаковые для каждого ряда. 
2. Выделить диаграмму и на вкладке «Конструктор» перейти к изменению ее типа. 
3. Выбрать вариант «Комбинированная» и второй вариант в списке — гистограмму с группировкой и график на вспомогательной оси. 
4. Настроить отображение — указать, для какого ряда будет построена вспомогательная ось, изменить виды диаграмм. 
5. Нажать «ОК» для перехода к дальнейшим настройкам. 

Теперь на графике будет две отличающихся друг от друга диаграммы, каждая из которых имеет свою шкалу с отдельными единицами измерения. Можно сделать так, чтобы на экране были, например, две похожих линии, выбрав соответствующие варианты на этапе изменения типа. Хотя это будет не так удобно даже при наличии легенды. 

Улитка Паскаля

Улитка Паскаля – плоская кривая. Ее можно определить как геометрическое место точек М и М₁, расположенных на прямых пучка с центром в точке О, лежащей на данной окружности радиуса R, и находящихся на равном расстоянии а по обе стороны от точки пересечения Р прямых пучка с окружностью – см. рис., – где а < 2R. Улитка Паскаля изображена на нем красной линией.Уравнение улитки Паскаля в полярных координатах имеет вид:

ρ = 2 Rcosφ + a,

где φ – полярный угол радиуса-вектора текущей точки.
Если а = 2R, то петля улитки Паскаля (сплошная линия внутри данной окружности на рис.) стягивается в точку, и улитка Паскаля вырождается в кардиоиду.

Если a > 2R, улитка Паскаля не имеет общих точек с данной окружностью (см. рис.).

х2у2Rx2a2x2y2аRа R а R S

при этом в случае а < 2R площадь внутренней петли считается по этой формуле дважды.
Улитка Паскаля – конхоида окружности диаметра 2 R; она же –  частный случай декартова овала; она же – эпитрохоида.

Кривая названа в честь знаменитого французского ученого Б. Паскаля, изучавшего ее в первой половине XVII в.

Шаг 2: Заполнение таблицы данными

Для заполнения таблицы следуйте этим шагам:

1. Введите число 1 в ячейку A1, которая будет располагаться в левом верхнем углу таблицы.
2. Переместитесь вправо на одну ячейку и введите число 1 в ячейку B1.
3. Переместитесь вниз на одну ячейку и введите число 1 в ячейку B2.
4. Переместитесь вправо на одну ячейку и введите сумму чисел, находящихся над этой ячейкой в столбце B — 1.
5. Продолжайте перемещаться вправо и вниз, вводя суммы чисел из предыдущего столбца, пока таблица не будет полностью заполнена.

После заполнения таблицы данными, вы должны увидеть улитку Паскаля, состоящую из чисел, которые верно отображают построение треугольника Паскаля.

Как построить кардиоиду в excel

1. Выделяем ячейку, в которой будет отображаться результат проведенных вычислений. Кликаем по значку «Вставить функцию», который размещен у строки формул.
2. Запускается окно Мастера функций. Выполняем переход в категорию «Статистические» или «Полный алфавитный перечень». В открывшемся списке производим поиск наименования «ПРЕДСКАЗ». Найдя его, выделяем, а затем щелкаем по кнопке «OK» в нижней части окна.
3. Мы перемещаемся к окну аргументов вышеуказанной функции. Она имеет всего три аргумента и соответствующее количество полей для их внесения.

Для расчета в таблицах часто требуется значения одного столбца разделить на данные второй колонки. Конечно, можно делить значение каждой ячейки тем способом, который указан выше, но можно эту процедуру сделать гораздо быстрее.

Если объяснять просто, то параметрическое уравнение (представление) — это ещё один способ выражения функции. Обычно они используются в задачах или уравнениях кинематики (задачах основ физики) для описания таких свойств, как траектория ракеты или орбита планеты, вращающейся вокруг массивного объекта.

Давайте рассмотрим следующую функцию, которая создаёт параболу.

Чтобы получить эту функцию, мы можем разложить (при помощи вузовской алгебры) вышеприведённое уравнение, изолировав X и Y и сгенерировав отдельный параметр, входящими данными которого является t, как показано в функции ниже.

По сути, если мы создадим таблицу этих двух интерпретаций функции, то они будут давать одинаковые ответы.

Обычная функция (сверху) и параметрическая функция (снизу)

По сути, когда мы используем две функции для генерирования координат X и Y, то можем, как вы увидите ниже, создать огромное количество графики, примеры которой представлены в этом посте. (Помните, что это всего один набор уравнений).

А теперь самое интересное — ниже я опишу процесс, благодаря которому сгенерировал все представленные в посте изображения.

Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».

Можно сделать даже проще, не запуская Мастер функций , а просто с клавиатуры вбить в пустую ячейку значение Н Д без кавычек. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!

Методом (половинного деления или итерации)(нужно выбрать правильный) найти корень уравнения (x — 3) / (x ^ 2 + 2) = 0 расположенный на отрезке с абсолютной погрешностью 10 ^ — 4 программа паскальи еще нужна блок схема.

Практическая работа в MS Excel «Графики»

Построить спираль Архимеда по следующим данным:— в столбце А – значения угла t в радианах от до 10 с шагом 0,2— в столбце В – значения r = 0,5*t— в столбце С – значения х = r*cos(t)— в столбце D – значения y = r*sin(t)— выделить значения в столбцах С и D и построить диаграмму (тип: точечная с гладкими кривыми)

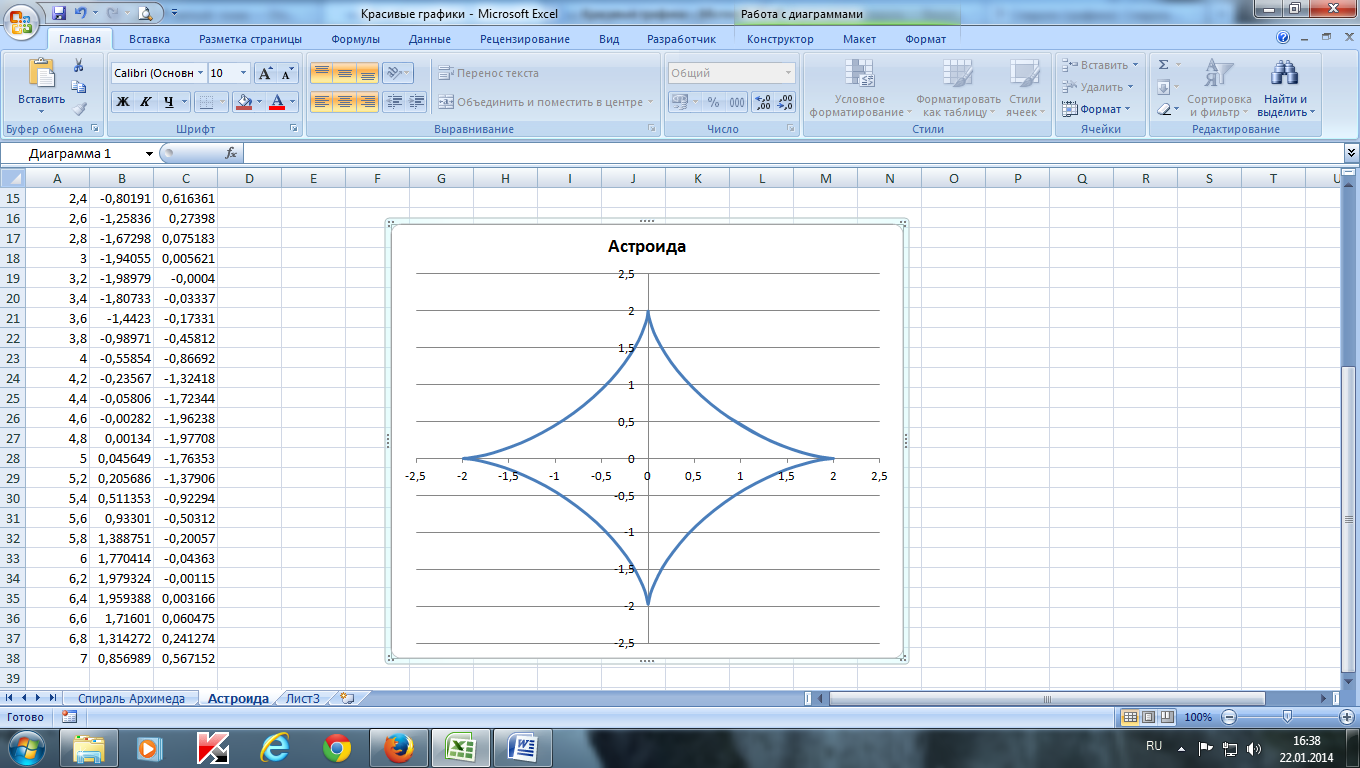
Построить астроиду по следующим данным:— в столбце А – значения угла t в радианах от до 7 с шагом 0,2— в столбце В – значения х = 2*(cos (t)) 3 — в столбце С – значения y = 2*(sin (t)) 3 — выделить значения в столбцах B и С и построить диаграмму (тип: точечная с гладкими кривыми)

Построить улитку Паскаля по следующим данным:— в столбце А – значения a от до 360 с шагом 10 (угол в градусах)— в столбце В – значения t = a*π/180 (угол в радианах) — в столбце С – значения p = cos(t)–0,5— в столбце D – значения x = p*cos(t)— в столбце Е – значения у = p*sin(t) — выделить значения в столбцах D и E и построить диаграмму (тип: точечная с гладкими кривыми)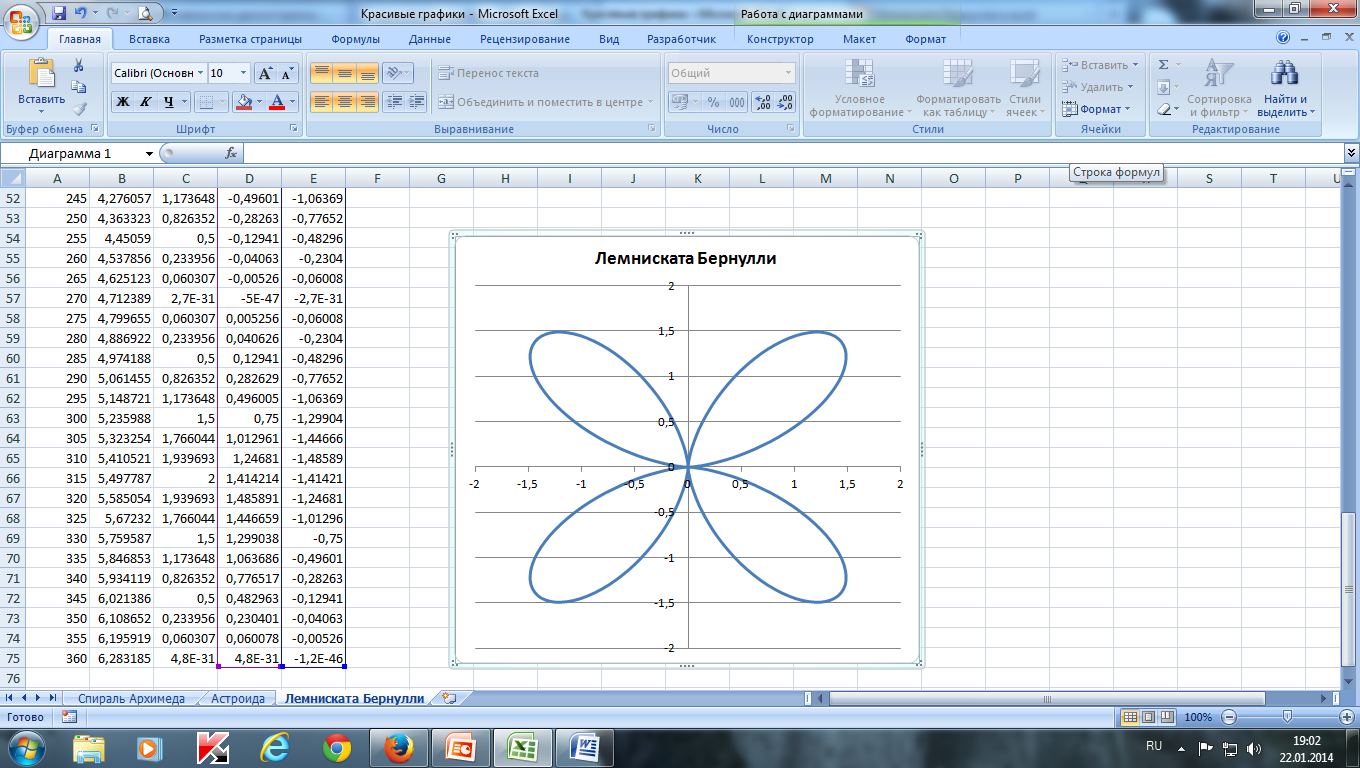

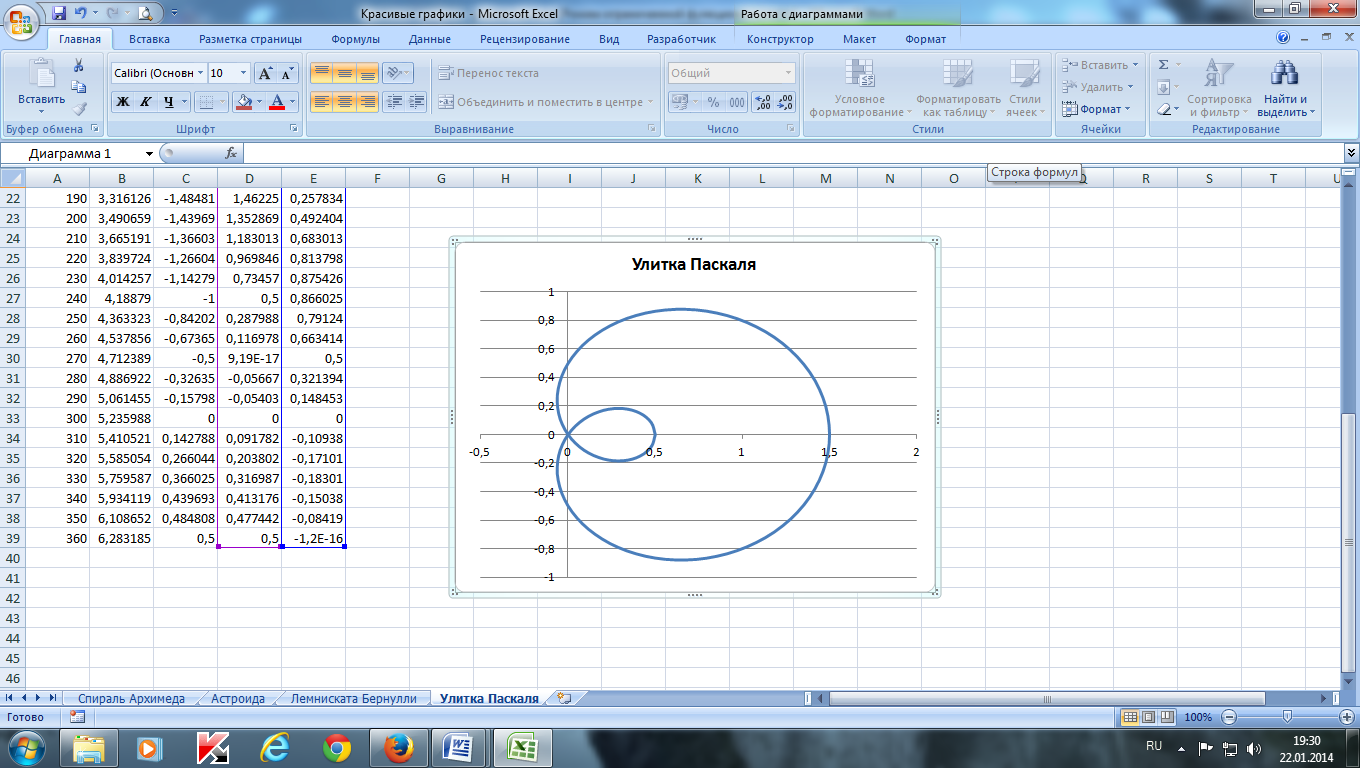
Построить лемнискату Бернулли по следующим данным:— в столбце А – значения a от до 360 с шагом 10 (угол в градусах)— в столбце В – значения t = a*π/180 (угол в радианах)— в столбце С – значения r = 2*sin(2*t) 2 — в столбце D – значения x = r*cos(t)— в столбце E – значения y = r*sin(t)— выделить значения в столбцах D и E и построить диаграмму (тип: точечная с гладкими кривыми)

Построить график в форме сердца по следующим данным:— в столбце А – значения a от до 360 с шагом 10 (угол в градусах)— в столбце В – значения t = a*π/180 (угол в радианах)— в столбце С – значения x = 16*(sin(t)) 3 — в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)— выделить значения в столбцах C и D и построить диаграмму (тип: точечная с гладкими кривыми)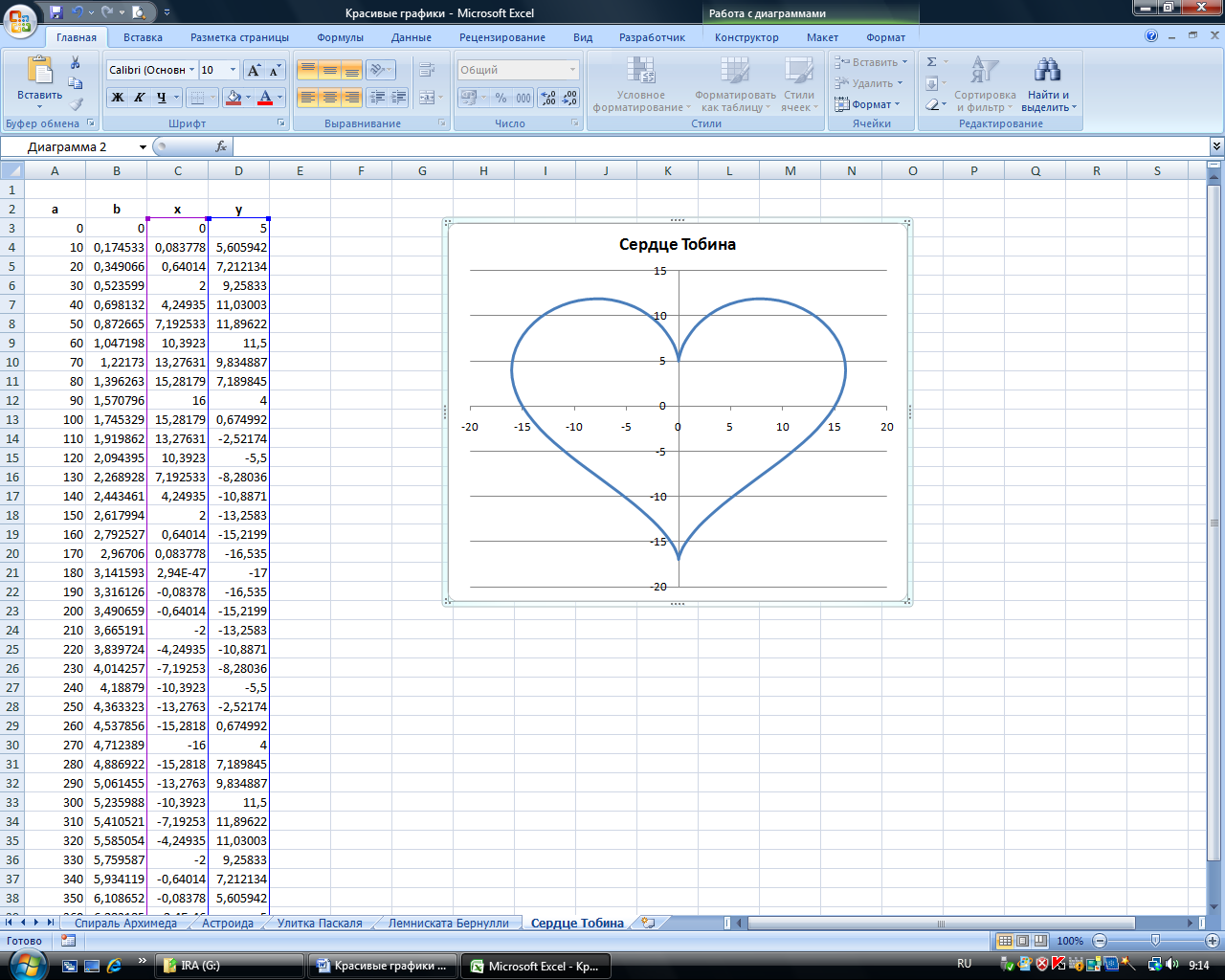

Практическая работа в MS Excel «Графики»

Работа в формате .docx

Просмотр содержимого документа «Практическая работа в MS Excel «Графики»»

Практическая работа «Красивые графики функций»

Построить спираль Архимеда по следующим данным:— в столбце А – значения угла t в радианах от до 10 с шагом 0,2— в столбце В – значения r = 0,5*t— в столбце С – значения х = r*cos(t)— в столбце D – значения y = r*sin(t)— выделить значения в столбцах С и D и построить диаграмму (тип: точечная с гладкими кривыми)

Построить астроиду по следующим данным:— в столбце А – значения угла t в радианах от до 7 с шагом 0,2— в столбце В – значения х = 2*(cos (t)) 3 — в столбце С – значения y = 2*(sin (t)) 3 — выделить значения в столбцах B и С и построить диаграмму (тип: точечная с гладкими кривыми)

Построить улитку Паскаля по следующим данным:— в столбце А – значения a от до 360 с шагом 10 (угол в градусах)— в столбце В – значения t = a*π/180 (угол в радианах) — в столбце С – значения p = cos(t)–0,5— в столбце D – значения x = p*cos(t)— в столбце Е – значения у = p*sin(t) — выделить значения в столбцах D и E и построить диаграмму (тип: точечная с гладкими кривыми)

Построить лемнискату Бернулли по следующим данным:— в столбце А – значения a от до 360 с шагом 10 (угол в градусах)— в столбце В – значения t = a*π/180 (угол в радианах)— в столбце С – значения r = 2*sin(2*t) 2 — в столбце D – значения x = r*cos(t)— в столбце E – значения y = r*sin(t)— выделить значения в столбцах D и E и построить диаграмму (тип: точечная с гладкими кривыми)

Построить график в форме сердца по следующим данным:— в столбце А – значения a от до 360 с шагом 10 (угол в градусах)— в столбце В – значения t = a*π/180 (угол в радианах)— в столбце С – значения x = 16*(sin(t)) 3 — в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)— выделить значения в столбцах C и D и построить диаграмму (тип: точечная с гладкими кривыми)

Источник

Гипоциклоида

Гипоцикло́ида — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.

, где — радиус неподвижной окружности, — радиус катящейся окружности.

К сожалению, у меня гипоциклоида пока что не получается, но, то что получается, мне очень нравится, думаю, и вам понравится.

Проект можно использовать на уроках математики при изучении функций гиперболы и параболы. А также можно работать над продолжением проекта – добавлять функции, изучаемые в школе. Конечно, мне очень хочется продолжить работу над проектом и создать проект построения функций в полярных координатах. И, как говорилось в начале проекта, может быть я смогу вывести формулу любви и построить её график.

При пользовании «Инфоуроком» вам не нужно платить за интернет!

Минкомсвязь РФ: «Инфоурок» включен в перечень социально значимых ресурсов .

Практическая работа «Красивые графики функций»

Варианты заданий для построения графиков.

1. Способы задания функций:

2. Исходные данные для функции, заданной в параметрическом виде или полярных координатах: a, b, l – параметры кривой.

Индивидуальные задания

1. Графики 3-х функций построить различными цветами на одном листе;

2. Каждый график построить на отдельном листе.

Источник теоретического материала:

Требования к отчету:

При работе в Excel:

1. Выполнить работу, согласно вашему заданию.

2. Каждый график рассчитывается и строится на отдельном листе книги.

3. Название листа книги должно соответствовать построенному графику

4. На каждом листе книги заполнить таблицу исходными данными, необходимыми для построения одного графика.

5. Проверять вводимые данные, на имеющиеся ограничения. (например а>0, при таких ограничениях значения ане должны быть отрицательными)

6. Выполнить все необходимые расчеты

7. Оформить внешний вид таблиц (заголовок, обрамление).

8. На каждом листе создать внедренный график, построенный на данных, рассчитанных в таблице. График должен иметь заголовок, и не иметь легенды.

9. После построения всех графиков создать диаграмму, расположенную на отдельном листе, на которую вынести все графики. Легенда обязательна.

10. В текстовом редакторе Word составить отчет, который включает задание, таблицы с необходимыми расчетами и соответствующие графики.

11. Ответить на вопросы преподавателя.

Создание отчета в Word:

2. Таблицы расчетов и внедренные графики, выполненные в Excel, должны быть вставлены в отчет с использованием связей (технология OLE)

Задание 7.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Работа в формате .docx

Просмотр содержимого документа «Практическая работа в MS Excel «Графики»»

Практическая работа «Красивые графики функций»

• Nokia браузер не может подключиться к веб сайту nokia

    

• Как открыть страницу в 1с

    

• Как убрать в ворде полоски между словами

    

• Настройка outlook через прокси

    

• Как убрать разделение слов на слоги в ворде