Основные понятия теории вероятностей с помощью excel

Как построить простой график

Для начала нужно создать какую-нибудь таблицу. Для примера будем исследовать зависимость затрат в разные дни отпуска.

Дальше нужно выполнить следующие действия.

1. Выделите всю таблицу целиком (включая шапку).

2. Перейдите на вкладку «Вставка». Кликните на иконку «Графики» в разделе «Диаграммы». Выберите тип «Линия».

3. В результате этого на листе появится простой график.

Благодаря этому графику мы можем увидеть, в какие дни были самые высокие затраты, а когда, наоборот, – минимальные. Кроме этого, по оси Y мы видим конкретные цифры. Диапазон проставляется автоматически, в зависимости от данных в таблице.

Схема независимых испытаний

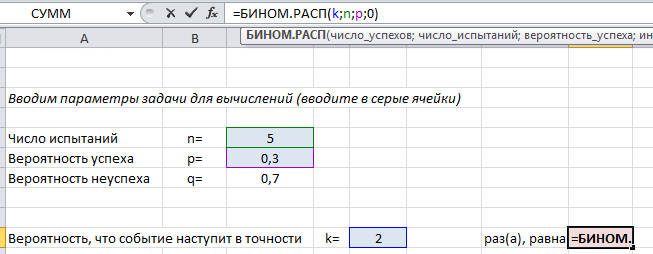
В общем виде схема повторных независимых испытаний записывается в виде задачи:

Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.

Эта вероятность вычисляется по формуле Бернулли:

$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$

Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:

• Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
• Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
• События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.

Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.

Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.

Несовместные и совместные события

Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.

Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно. 

Несовместные события — такие события, появление одного из которых исключает появление другого. 

Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности. 

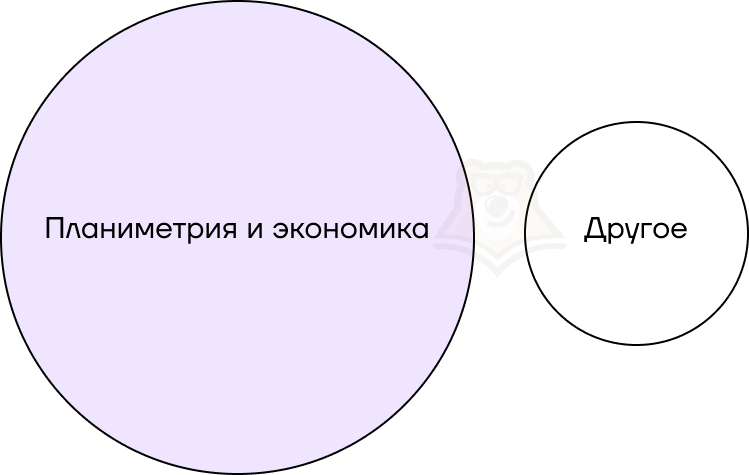
Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.

Сформулируем определение суммы вероятностей двух несовместных событий. 

Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:\(P(A \cup B) = P(A) + P(B)\)

Если существуют несовместные события, то существуют и совместные. 

Совместные события — события, наступление одного из которых не исключает наступления другого. 

В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят?  Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет. 

Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”. 

Найдем вероятность события А: \(\frac{1}{6}\). 

Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна \(\frac{3}{6} = \frac{1}{2}\)

Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А. 

Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги. 

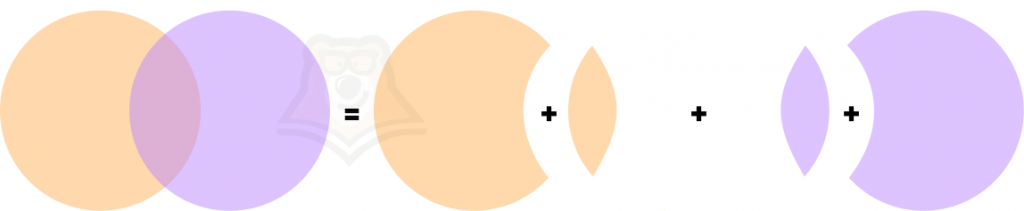
А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок. 

Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:\(P(A \cup B) = P(A) + P(B) — P(A \cap B)\)

В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике. 

Теорема Бернулли

Предположим, что мы произвели большое число п испытаний Бернулли с вероятностью успеха р. По числу полученных успехов определим наблюденную частоту Спрашивается, как сильно может отличаться наблюденная частота успеха от вероятности успеха р? Ясно, что, вообще говоря, частота может принимать любые значения от 0 до 1. Так, мы вполне можем получить в n испытаниях одни неудачи. Но, как мы знаем, вероятность такого события равна и при больших n она будет весьма мала. Поэтому естественно ожидать, что при больших n частота с большой вероятностью группируется вокруг вероятности р, что мы сейчас и установим, исходя из интегральной теоремы Муавра-Лапласа.

Пусть — любое сколь угодно малое число, а событие А заключается в том, что наблюдаемая в п испытаниях частота отличается от вероятности по модулю не больше чем на Иными словами, событие А происходит тогда и только тогда, когда число успехов в п испытаниях заключено в пределах от Теперь, если п велико, то мы можем воспользоваться интегральной теоремой Муавра-Лапласа, в которой и, значит,

Но с ростом В свою очередь, Поэтому, каково бы ни было с ростом п вероятность того, что частота отличается от вероятности р не более чем на стремится к 1.

Установленный нами факт предельного постоянства частоты впервые был обнаружен Я. Бернулли, он носит название (слабого) закона больших чисел или теоремы Бернулли. Закон больших чисел и его многочисленные обобщения являются звеном, позволяющим связать аксиоматическое построение теории вероятностей с эмпирическим законом постоянства частоты, с которого мы начали путешествие в теорию вероятностей. Именно он позволяет обосновать то широкое применение методов теории вероятностей на практике, которое мы имеем в настоящее время.

Однако если произвести более строгий логический анализ, то окажется, что слабый закон больших чисел также не вполне удовлетворяет нашим исходным предпосылкам, поскольку когда мы говорим о стабильности частоты, то имеем в виду процесс, протекающий во времени. Слабый закон больших чисел утверждает только, что при большом, но фиксированном числе испытаний частота мало отличается от вероятности. Слабый закон больших чисел еще не исключает значительных, но редких отклонений частоты от вероятности при последовательном проведении испытаний. Здесь мы пока только отметим, что имеет место усиленный закон больших чисел, который в определенной степени устраняет это логическое несовершенство слабого закона больших чисел.

Более подробно закон больших чисел, как и интегральная теорема Муавра-Лапласа, будут обсуждены нами в гл. 8, посвященной предельным теоремам теории вероятностей.

Генерация случайных чисел. Биномиальное распределение

Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий p
, которая является характеристикой нашего производственного процесса. Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же p
осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.

Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении Альфа
. Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке, p
«скорее всего» увеличилось. Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.

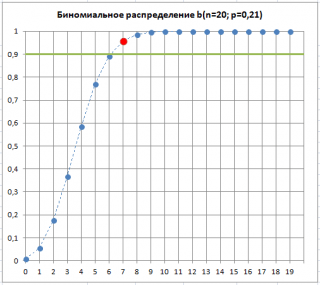
Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать бо
льший процент бракованных изделий.

Примечание
: До MS EXCEL 2010 в EXCEL была функция КРИТБИНОМ()
, которая эквивалентна БИНОМ.ОБР()
. КРИТБИНОМ()
оставлена в MS EXCEL 2010 и выше для совместимости.

Генерация случайных чисел. Биномиальное распределение

Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий p
, которая является характеристикой нашего производственного процесса. Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же p
осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.

Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении Альфа
. Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке, p
«скорее всего» увеличилось. Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.

Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать бо
льший процент бракованных изделий.

Примечание
: До MS EXCEL 2010 в EXCEL была функция КРИТБИНОМ()
, которая эквивалентна БИНОМ.ОБР()
. КРИТБИНОМ()
оставлена в MS EXCEL 2010 и выше для совместимости.

Расчет в Excel трубопроводов по формулам теоретической гидравлики.

Рассмотрим порядок и формулы расчета в Excel на примере прямого горизонтального трубопровода длиной 100 метров из трубы ø108 мм с толщиной стенки 4 мм.

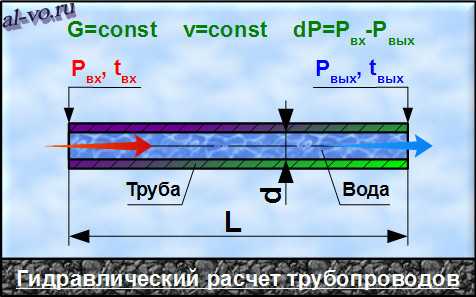
Исходные данные:

1. Расход воды через трубопровод G в т/час вводим

в ячейку D4: 45,000

2. Температуру воды на входе в расчетный участок трубопровода  t_вхв °C заносим

в ячейку D5: 95,0

3. Температуру воды на выходе из расчетного участка трубопровода  t_выхв °C записываем

в ячейку D6: 70,0

4. Внутренний диаметр трубопровода  dв мм вписываем

в ячейку D7: 100,0

5. Длину трубопровода  Lв м записываем

в ячейку D8: 100,000

6. Эквивалентную шероховатость внутренних поверхностей труб  ∆ в мм вносим

в ячейку D9:  1,000

Выбранное значение эквивалентной шероховатости соответствует стальным старым заржавевшим трубам, находящимся в эксплуатации много лет.

Эквивалентные шероховатости для других типов и состояний труб приведены на листе «Справка» расчетного файла Excel«gidravlicheskiy-raschet-truboprovodov.xls», ссылка на скачивание которого дана в конце статьи.

7. Сумму коэффициентов местных сопротивлений  Σ(ξ) вписываем

в ячейку D10: 1,89

Мы рассматриваем пример, в котором местные сопротивления присутствуют в виде стыковых сварных швов (9 труб, 8 стыков).

Для ряда основных типов местных сопротивлений данные и формулы расчета представлены на листах «Расчет коэффициентов» и «Справка» файла Excel «gidravlicheskiy-raschet-truboprovodov.xls».

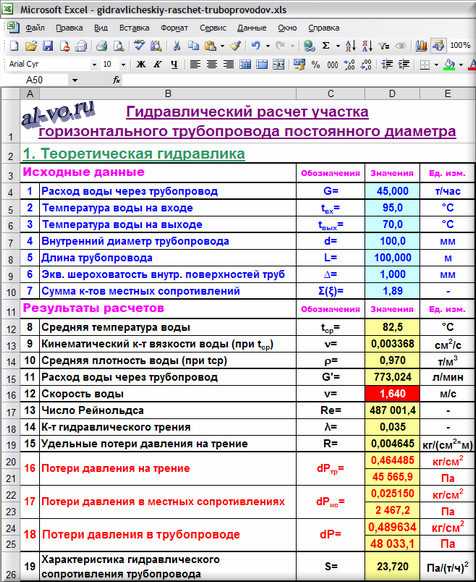
Результаты расчетов:

8.Среднюю температуру воды t_ср в °C вычисляем

в ячейке D12: =(D5+D6)/2 =82,5

t_ср=(t_вх+t_вых)/2

9.Кинематический коэффициент вязкости воды n в cм2/с при температуреt_ср рассчитываем

в ячейке D13: =0,0178/(1+0,0337*D12+0,000221*D12^2) =0,003368

n=0,0178/(1+0,0337*t_ср+0,000221*t_ср2)

10.Среднюю плотность воды ρ в т/м3 при температуреt_ср вычисляем

в ячейке D14: =(-0,003*D12^2-0,1511*D12+1003,1)/1000 =0,970

ρ=(-0,003*t_ср2-0,1511*t_ср+1003, 1)/1000

11.Расход воды через трубопровод G’ в л/мин пересчитываем

в ячейке D15: =D4/D14/60*1000 =773,024

G’=G*1000/(ρ*60)

Этот параметр пересчитан нами в других единицах измерения для облегчения восприятия величины расхода.

12.Скорость воды в трубопроводе vв м/с вычисляем

в ячейке D16: =4*D4/D14/ПИ()/(D7/1000)^2/3600 =1,640

v=4*G/(ρ*π*(d/1000)2*3600)

К ячейкеD16 применено условное форматирование. Если значение скорости не попадает в диапазон 0,25…1,5 м/с, то фон ячейки становится красным, а шрифт белым.

Предельные скорости движения воды приведены на листе «Справка» расчетного файла Excel «gidravlicheskiy-raschet-truboprovodov.xls».

13.Число Рейнольдса Reопределяем

в ячейке D17: =D16*D7/D13*10 =487001,4

Re=v*d*10n

14.Коэффициент гидравлического трения λрассчитываем

в ячейке D18: =ЕСЛИ(D17<=2320;64/D17;ЕСЛИ(D17<=4000; 0,0000147*D17;0,11* (68/D17+D9/D7)^0,25)) =0,035

λ=64Re                             при Re≤2320

λ=0,0000147*Re               при 2320≤Re≤4000

λ=0,11*(68/Re+∆/d)0,25  при Re≥4000

15.Удельные потери давления на трение Rв кг/(см2*м)вычисляем

в ячейке D19: =D18*D16^2*D14/2/9,81/D7*100 =0,004645

R=λ*v2*ρ*100/(2*9,81*d)

16.Потери давления на трение dP_трв кг/см2 и Па находим соответственно

в ячейке D20: =D19*D8 =0,464485

dP_тр=R*L

и в ячейке D21: =D20*9,81*10000 =45565,9

dP_тр=dP_тр*9,81*10000

17.Потери давления в местных сопротивлениях dP_мсв кг/см2 и Па находим соответственно

в ячейке D22: =D10*D16^2*D14*1000/2/9,81/10000 =0,025150

dP_мс=Σ(ξ)*v2*ρ/(2*9,81*10)

и в ячейке D23: =D22*9,81*10000 =2467,2

dP_тр=dP_мс*9,81*10000

18.Расчетные потери давления в трубопроводе dPв кг/см2 и Па находим соответственно

в ячейке D24: =D20+D22 =0,489634

dP=dP_тр+dP_мс

и в ячейке D25: =D24*9,81*10000 =48033,1

dP=dP*9,81*10000

19.Характеристику гидравлического сопротивления трубопровода Sв Па/(т/ч)2 вычисляем

в ячейке D26: =D25/D4^2 =23,720

S=dPG2

Гидравлический расчет в Excel трубопровода по формулам теоретической гидравлики выполнен!

Схема независимых испытаний

В общем виде схема повторных независимых испытаний записывается в виде задачи:

Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.

Эта вероятность вычисляется по формуле Бернулли:

$$ P_n(k)=C_n^k \cdot p^k \cdot (1-p)^ =C_n^k \cdot p^k \cdot q^ . \qquad(1) $$

Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:

• Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
• Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
• События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.

Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.

Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.

Математическая статистика

При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):

Обработка выборки: формулы Excel

Вычисляет среднее абсолютных значений отклонений точек данных от среднего.

Вычисляет среднее арифметическое аргументов.

Вычисляет среднее геометрическое.

Вычисляет среднее гармоническое.

Определяет эксцесс множества данных.

Находит медиану заданных чисел.

Определяет значение моды множества данных.

Определяет квартиль множества данных.

Определяет асимметрию распределения.

Оценивает стандартное отклонение по выборке.

Оценивает дисперсию по выборке.

Законы распределений: формулы Excel

Определяет интегральную функцию плотности бета-вероятности.

Определяет обратную функцию к интегральной функции плотности бета-вероятности.

Вычисляет одностороннюю вероятность распределения хи-квадрат.

Вычисляет обратное значение односторонней вероятности распределения хи-квадрат.

Находит экспоненциальное распределение.

Находит F-распределение вероятности.

Определяет обратное значение для F-распределения вероятности.

Находит преобразование Фишера.

Находит обратное преобразование Фишера.

Находит обратное гамма-распределение.

Выдает распределение Пуассона.

Выдает t-распределение Стьюдента.

Выдает обратное t-распределение Стьюдента.

Выдает распределение Вейбулла.

Другое (корреляция, регрессия и т.п.)

Определяет доверительный интервал для среднего значения по генеральной совокупности.

Находит коэффициент корреляции между двумя множествами данных.

Подсчитывает количество чисел в списке аргументов.

Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона.

Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек.

Вычисляет значение линейного тренда.

Находит параметры линейного тренда.

Определяет коэффициент корреляции Пирсона.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

σ2 – дисперсия;

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X < b) = Ф(b) – Ф(a)

Вычисление вероятностей с использованием функций MS EXCEL

1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).

2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.

3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА) .

Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.

Распределение Пуассона в Excel: применение и формулы

В Excel распределение Пуассона может быть использовано для анализа данных по поступлению в систему заявок, количеству ошибок на производстве, частоте возникновения аварий и других случайных явлений.

Для вычисления значения функции распределения Пуассона в Excel используется функция POISSON.DIST. Эта функция принимает три аргумента: значение, среднее значение и логический параметр, указывающий, следует ли использовать значение функции распределения (TRUE) или значение плотности вероятности (FALSE).

Например, чтобы вычислить вероятность того, что в заданном интервале времени произойдет ровно 3 события при среднем значении 2, можно использовать следующую формулу:

=POISSON.DIST(3,2,FALSE)

Функция POISSON.DIST возвращает значение вероятности для заданных аргументов. В данном случае, вероятность составляет около 18.29%.

Также в Excel есть функции POISSON.INV и POISSON.TEST, которые используются для обратных расчетов и тестирования гипотезы соответственно.

Распределение Пуассона является очень полезным инструментом для анализа и моделирования случайных событий с постоянной интенсивностью. С помощью функций распределения Пуассона в Excel можно осуществлять вычисления и проводить статистический анализ без необходимости в использовании дополнительного программного обеспечения.

Лабораторная работа ‘MS Excel. Построение графиков и диаграмм’

«Построение и редактирование различных типов диаграмм в MS Excel».

Цель урока: Закрепить умения по построению различных типов диаграмм, редактированию и изменению их типов.

Оснащение урока: ПК, MS Excel, задания для практического занятия

Построить функцию, заданную уравнением: , .

Для построения графика функции используется тип диаграммы Точечная. Выделяется только диапазон значений x и y.

Построим таблицу и произведем расчеты:

Для получения полной трехлепестковой розы значение fi должно быть от 0 до 3,2.

Формулы для вычисления:

Построить график функции: (fi выбираем из интервала с шагом 0,05)

Построить график функции (Декартов лист): . Fi из диапазона -0,15 до 2 шагом 0,05.

Построить Верьсьеру: . Принять t от -5 до 5 шагом 0,3.

Построить Лемнискату Бернулли: . Fi возьмите из диапазона от -3 до 0 с шагом 0,1.