Как использовать критерий Фишера в Excel
Критерий Фишера (англ. Fisher’s exact test) — это метод, который используется для проверки значимости статистических связей между двумя категориальными переменными. Он часто применяется в медицине, биологии и других областях при исследовании взаимосвязей между двумя группами. Вы можете легко применить критерий Фишера в Excel, используя встроенную функцию.
Начните с выбора двух таблиц сопряженности на листе Excel. Одна таблица должна содержать данные наблюдаемых значений, а вторая — ожидаемых значений. Затем вы можете использовать функцию FISHER.TEST(), чтобы вычислить вероятность получения таких же либо более значимых результатов, если бы связь между этими двумя переменными была случайной.
Вы также можете использовать условное форматирование в Excel, чтобы визуализировать результаты вашей таблицы сопряженности. Раскрасьте ячейки в соответствии с уровнем значимости, чтобы быстро определить, какие ячейки являются статистически значимыми, а какие нет.
Критерий Фишера — это инструмент, необходимый при исследовании различных взаимосвязей в категориальных данных. Использование этого метода в Excel позволяет быстро и удобно определить статистическую значимость этих связей, а также визуализировать результаты.
-Критерий стьюдента для уравнения множественной регрессии.
Частный
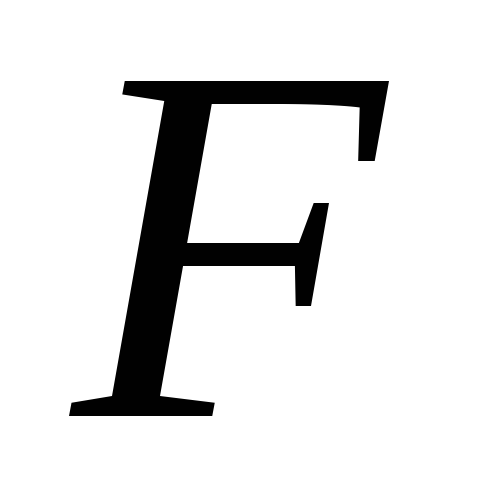 -критерий
-критерий
оценивает значимость коэффициентов
чистой регрессии. Зная величину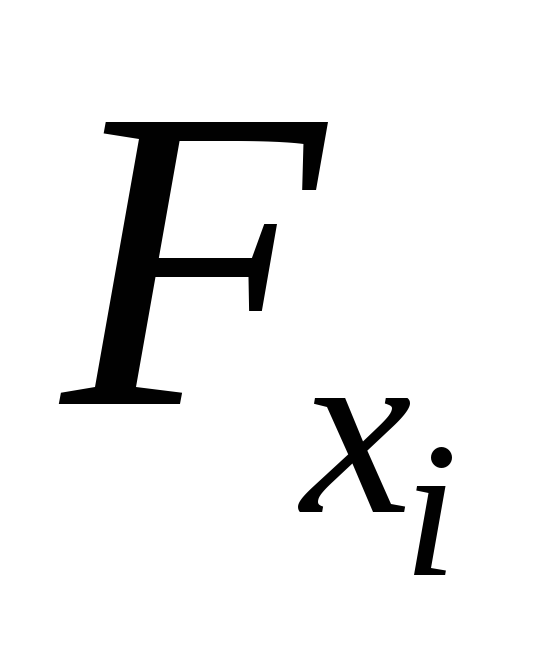 ,
,
можно определить и-критерий
для коэффициента регрессии при-м
факторе,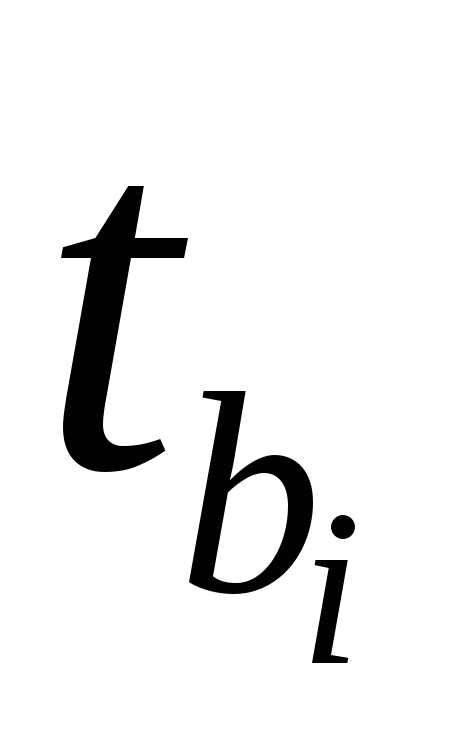 ,
,
а именно:
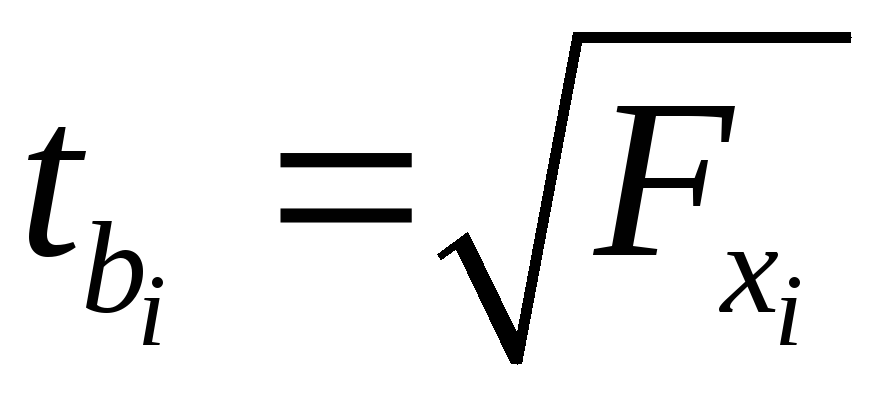 .
.
(2.24)
Оценка значимости коэффициентов чистой
регрессии по
-критерию
Стьюдента может быть проведена и без
расчета частных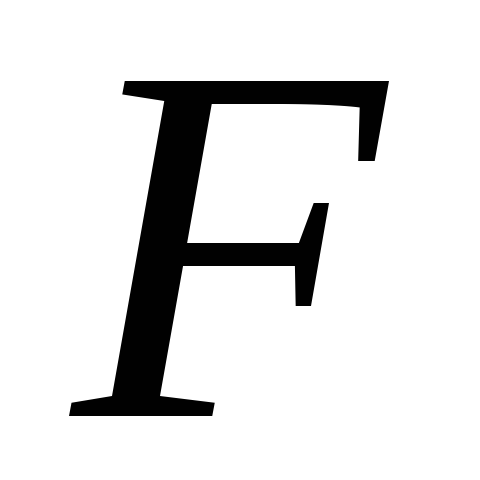 -критериев.
-критериев.
В этом случае, как и в парной регрессии,
для каждого фактора используется
формула:
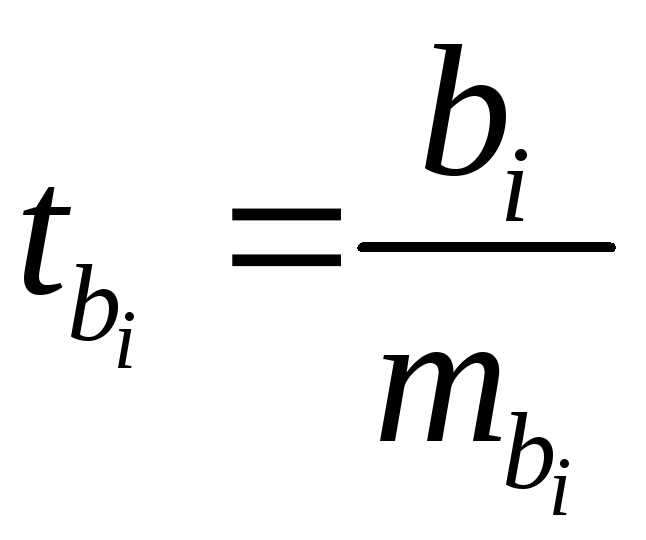 ,
,
(2.25)
где
 – коэффициент чистой регрессии при
– коэффициент чистой регрессии при
факторе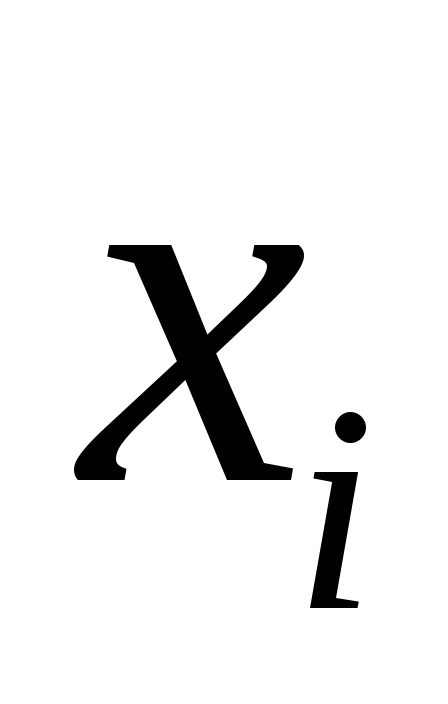 ,
,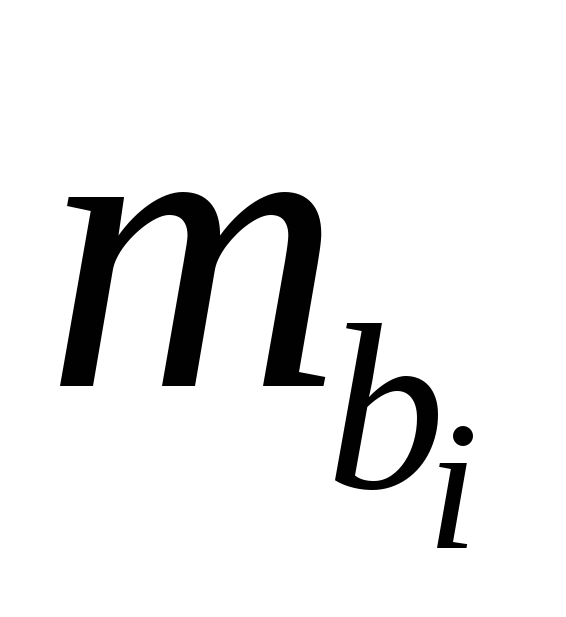 – средняя квадратическая (стандартная)
– средняя квадратическая (стандартная)
ошибка коэффициента регрессии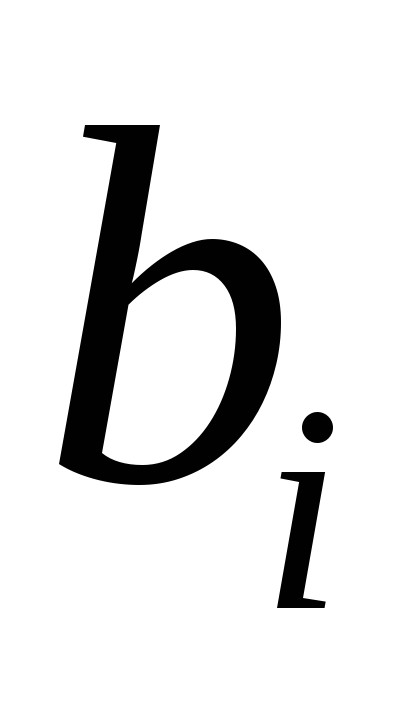 .
.
Для уравнения множественной регрессии
средняя квадратическая ошибка коэффициента
регрессии может быть определена по
следующей формуле:
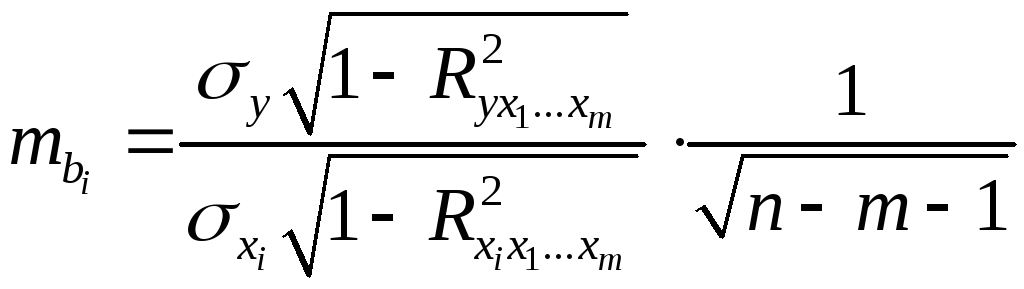 ,
,
(2.26)
где
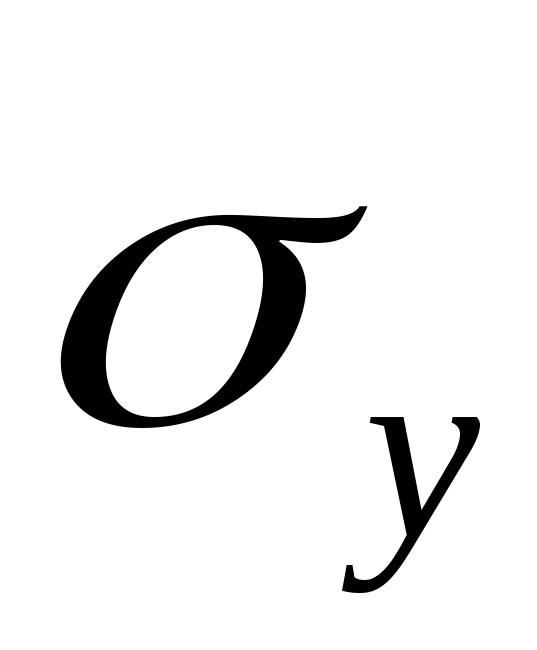
 ,
,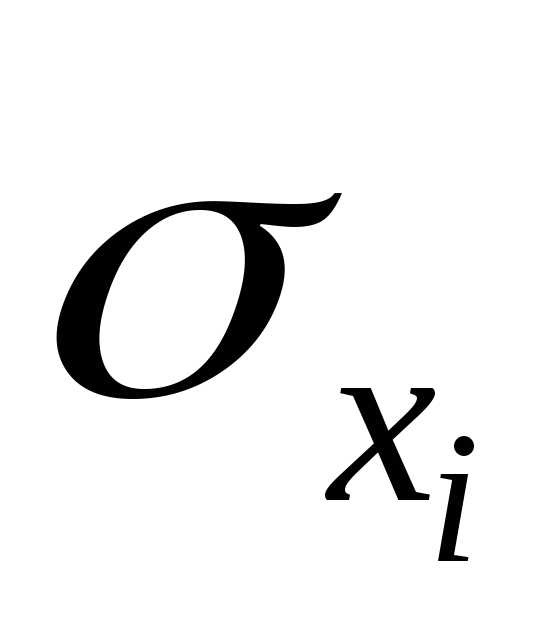 – среднее квадратическое отклонение
– среднее квадратическое отклонение
для признака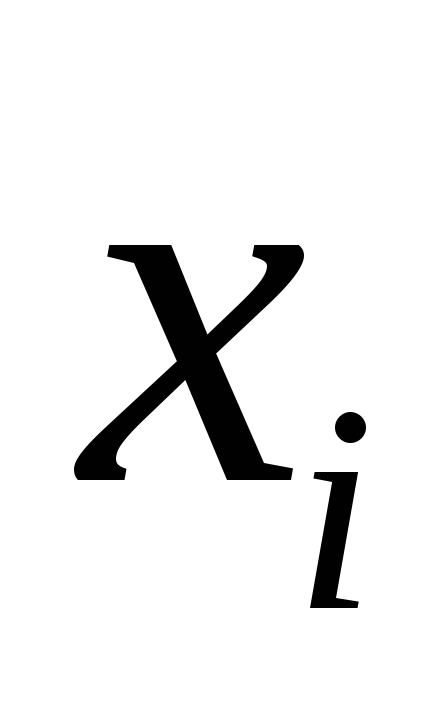 ,
, – коэффициент детерминации для
– коэффициент детерминации для
уравнения множественной регрессии,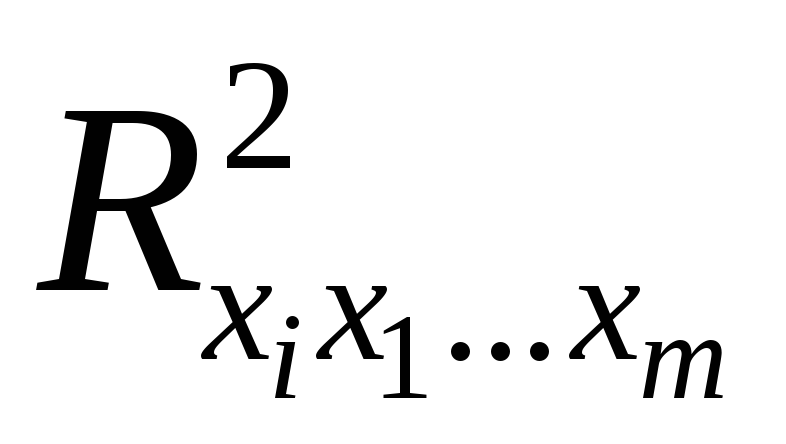 – коэффициент детерминации для
– коэффициент детерминации для
зависимости фактора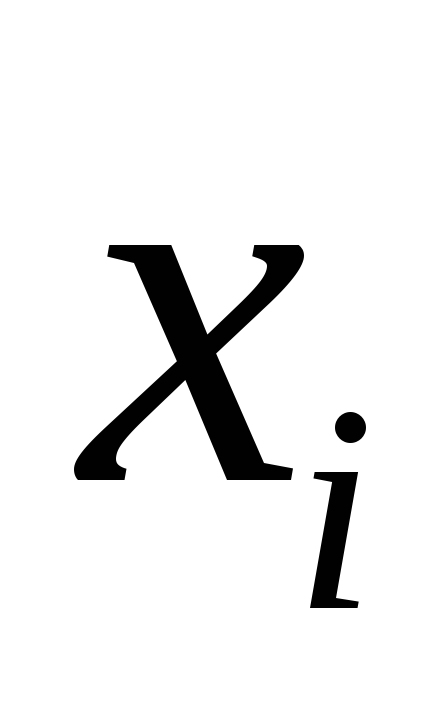 со всеми другими факторами уравнения
со всеми другими факторами уравнения
множественной регрессии;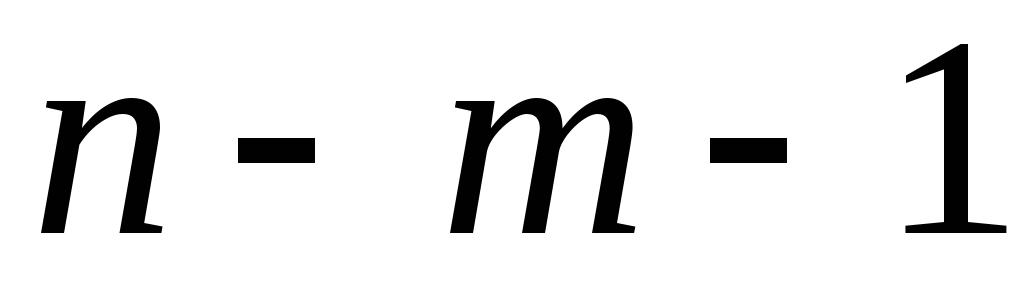 – число степеней свободы для остаточной
– число степеней свободы для остаточной
суммы квадратов отклонений.
Как видим, чтобы воспользоваться данной
формулой, необходимы матрица межфакторной
корреляции и расчет по ней соответствующих
коэффициентов детерминации
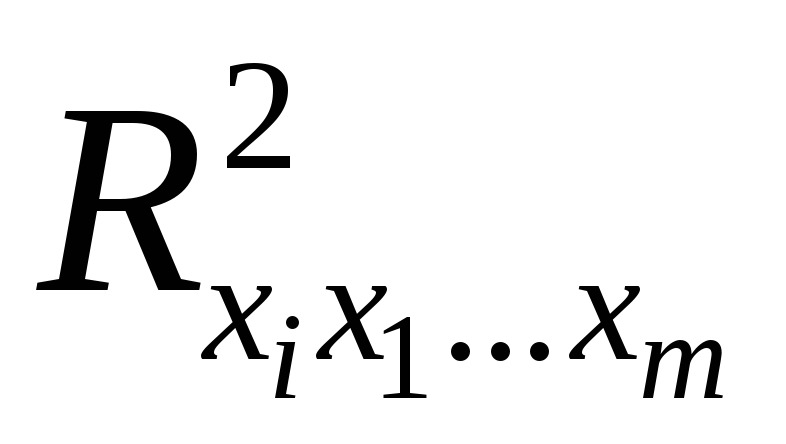 .
.
Так, для уравнения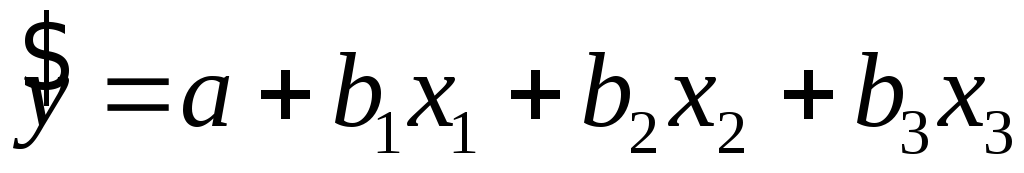 оценка значимости коэффициентов
оценка значимости коэффициентов
регрессии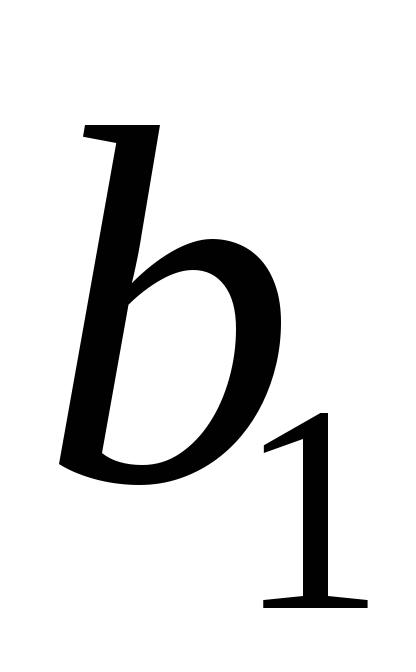 ,
,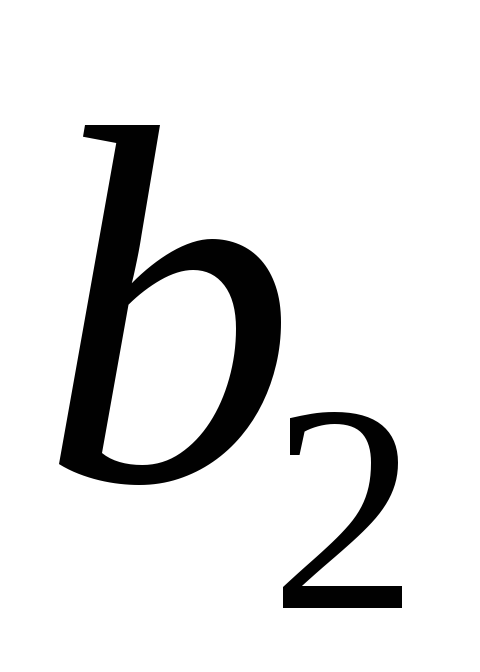 ,
,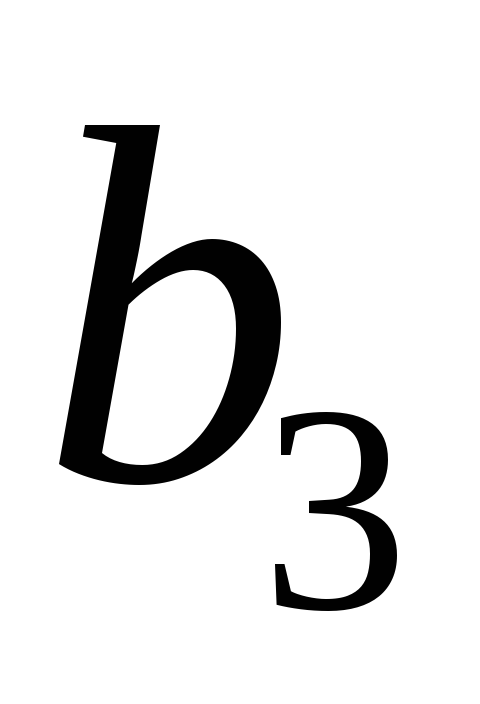 предполагает расчет трех межфакторных
предполагает расчет трех межфакторных
коэффициентов детерминации: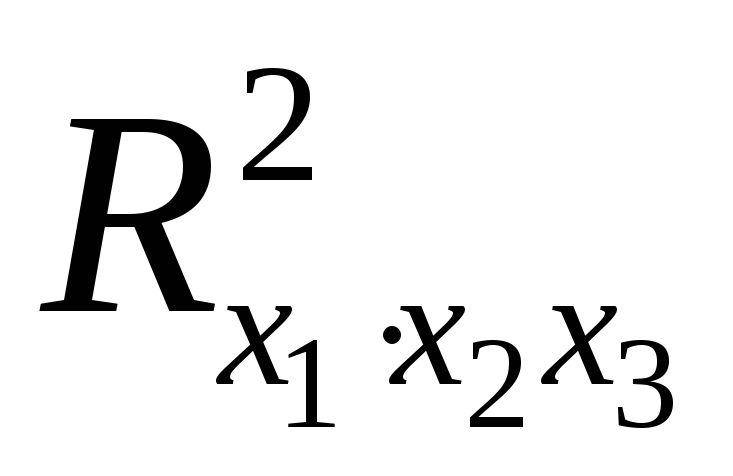 ,
,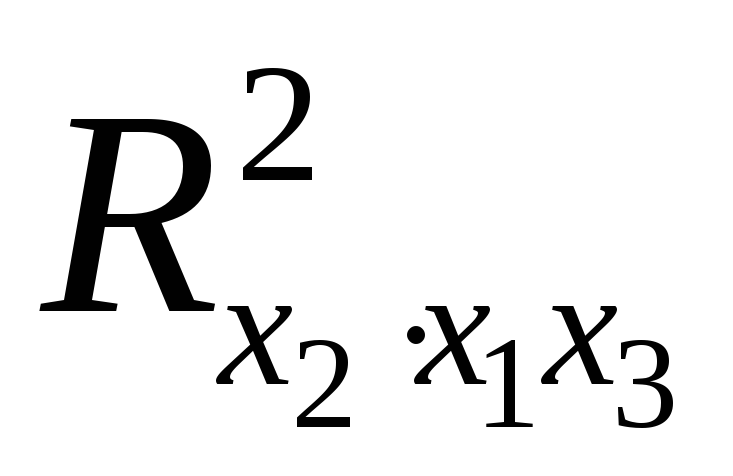 ,
,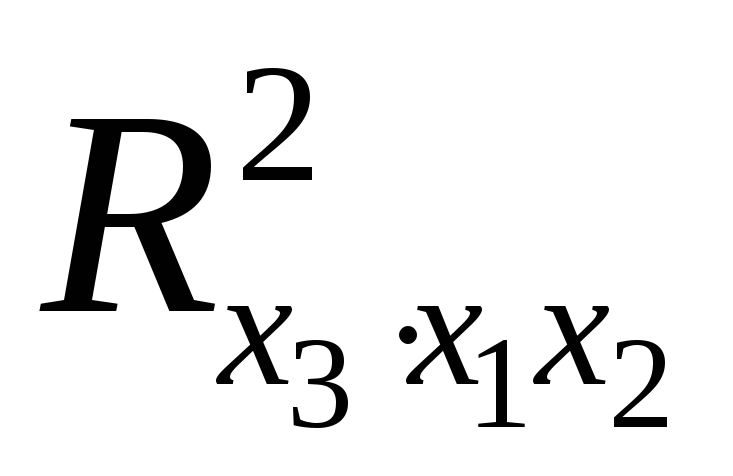 .
.
Взаимосвязь показателей частного
коэффициента корреляции, частного
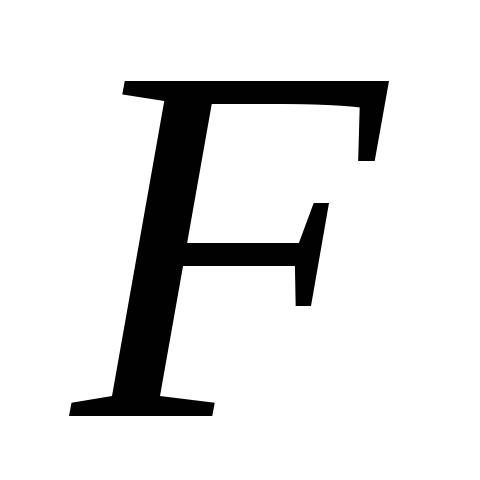 -критерия
-критерия
и-критерия
Стьюдента для коэффициентов чистой
регрессии может использоваться в
процедуре отбора факторов. Отсев факторов
при построении уравнения регрессии
методом исключения практически можно
осуществлять не только по частным
коэффициентам корреляции, исключая на
каждом шаге фактор с наименьшим незначимым
значением частного коэффициента
корреляции, но и по величинам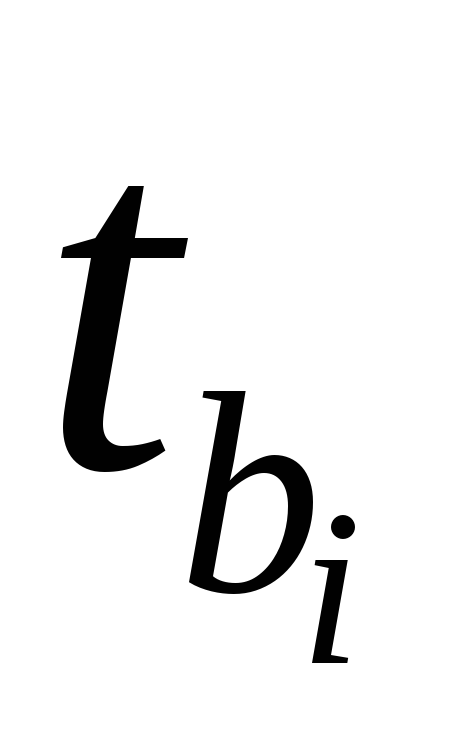 и
и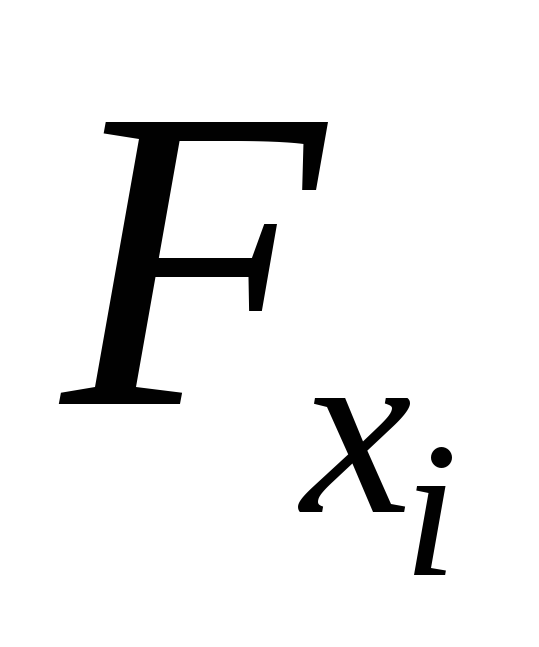 .
.
Частный -критерий
-критерий
широко используется и при построении
модели методом включения переменных и
шаговым регрессионным методом.
На данном примере рассмотрим, как оценивается надежность полученного уравнение регрессии. Этот же тест используется для проверки гипотезы о том, что коэффициенты регрессии одновременно равны нулю, a=0 , b=0 . Другими словами, суть расчетов — ответить на вопрос: можно ли его использовать для дальнейшего анализа и прогнозов?
Для установления сходства или различия дисперсий в двух выборках используйте данный t-критерий .
Итак, целью анализа является получение некоторой оценки, с помощью которой можно было бы утверждать, что при некотором уровне α полученное уравнение регрессии — статистически надежно. Для этого используется коэффициент детерминации R 2
.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k 1 =(m) и k 2 =(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H 0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3
Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2 (или через функцию Excel FРАСПОБР(вероятность;1;n-2)).
F табл — это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α — вероятность отвергнуть правильную гипотезу при условии, что она верна
Обычно α принимается равной 0,05 или 0,01.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k 1 =1 и k 2 =48, F табл = 4
Выводы
: Поскольку фактическое значение F > F табл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна
)
.
Как выполнить точный тест Фишера в Excel
Точный критерий Фишера используется для определения того, существует ли значительная связь между двумя категориальными переменными. Обычно он используется в качестве альтернативы критерию независимости хи-квадрат, когда количество одной или нескольких ячеек в таблице 2 × 2 меньше 5.
В этом руководстве объясняется, как выполнить точный критерий Фишера в Excel.
Пример: точный критерий Фишера в Excel
Предположим, мы хотим знать, связан ли пол с предпочтениями политической партии в конкретном колледже. Чтобы изучить это, мы случайным образом опрашиваем 25 студентов в кампусе. Количество студентов, которые являются демократами или республиканцами, в зависимости от пола, показано в таблице ниже:
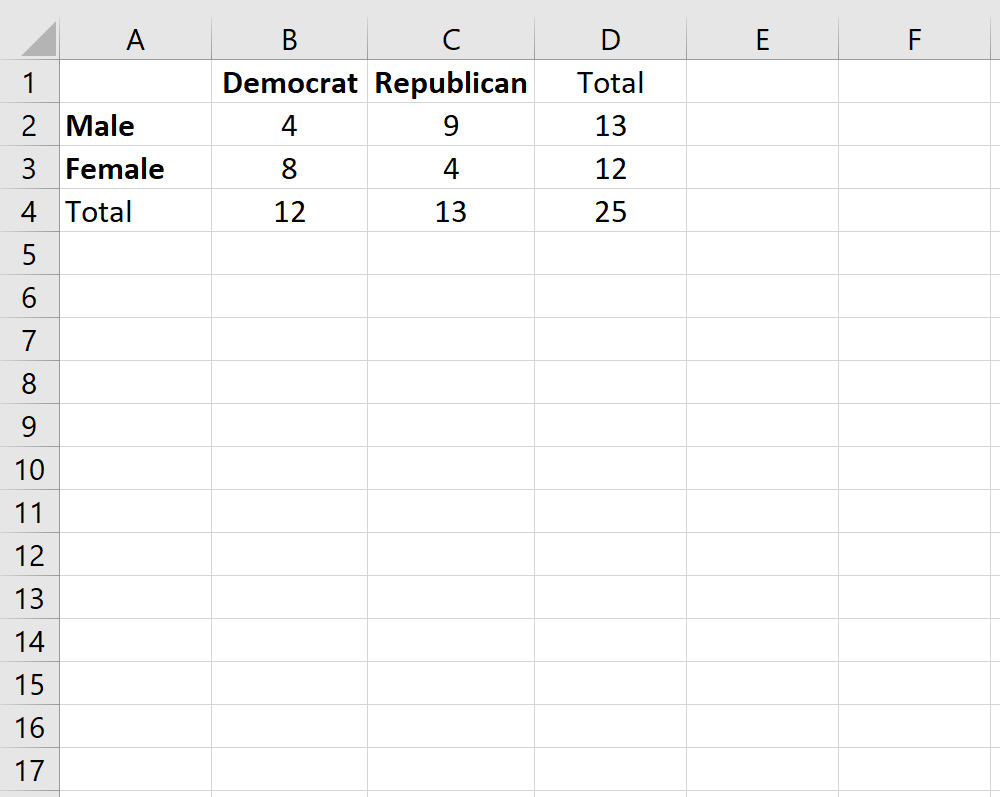
Чтобы определить, существует ли статистически значимая связь между полом и предпочтениями политической партии, мы можем выполнить точный тест Фишера.
Хотя в Excel нет встроенной функции для выполнения этого теста, мы можем использовать гипергеометрическую функцию для выполнения теста, которая использует следующий синтаксис:
=HYPGEOM.DIST(выборка_s, число_выборка, совокупность_s, число_население, кумулятивный)
- sample_s = количество «успехов» в образце
- number_sample = размер выборки
- населения_s = количество «успехов» в популяции
- number_pop = численность населения
- cumulative = если TRUE, возвращает кумулятивную функцию распределения; если FALSE, это возвращает функцию массы вероятности. Для наших целей мы всегда будем использовать TRUE.
Чтобы применить эту функцию к нашему примеру, мы выберем для использования одну из четырех ячеек в таблице 2×2. Подойдет любая ячейка, но в этом примере мы будем использовать верхнюю левую ячейку со значением «4».
Далее мы заполним следующие значения для функции:
= HYPGEOM.DIST (значение в отдельной ячейке, общее количество столбцов, общее количество строк, общий размер выборки, TRUE)
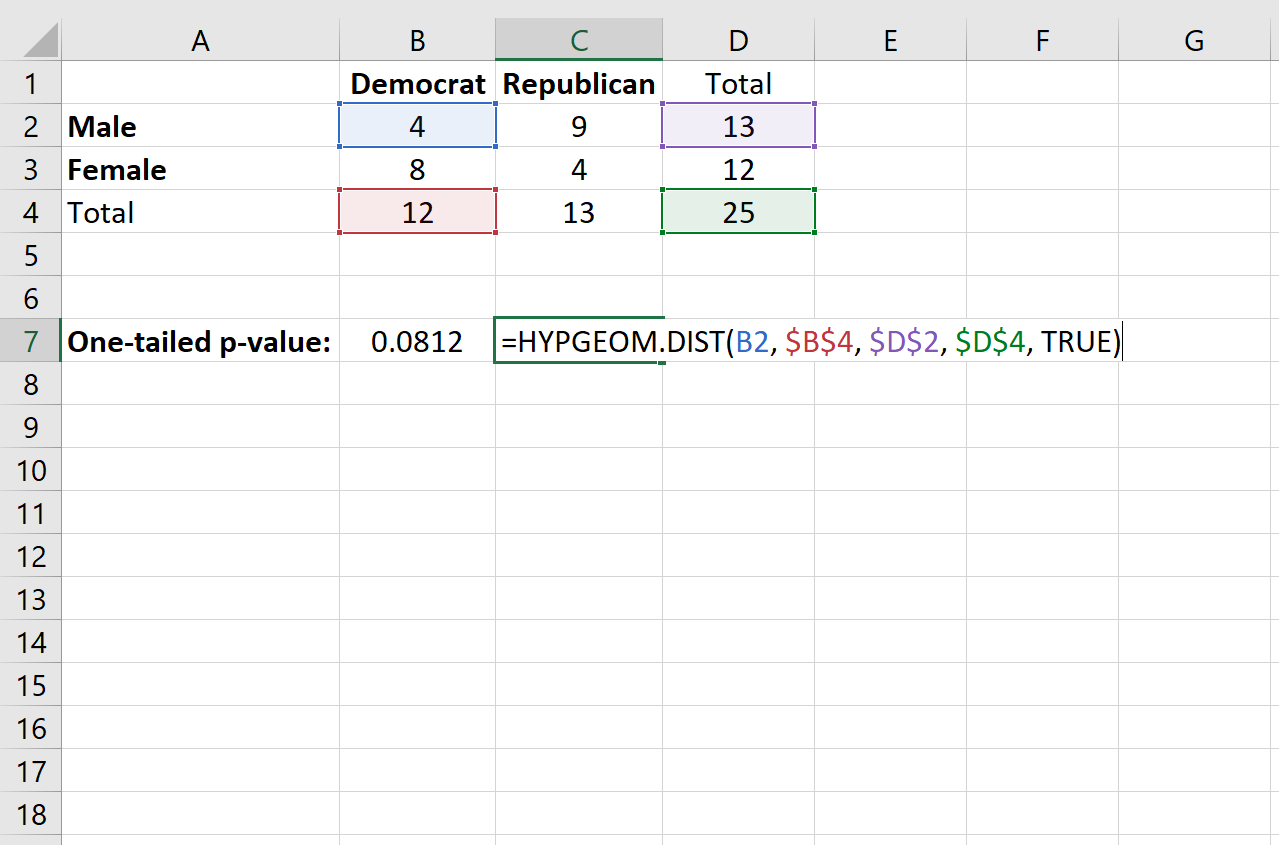
Это дает одностороннее p-значение 0,0812 .
Чтобы найти двустороннее p-значение для теста, мы сложим вместе следующие две вероятности:
- Вероятность получения x «успехов» в интересующей нас ячейке. В нашем случае это вероятность получения 4 успехов (мы уже нашли эту вероятность равной 0,0812).
- 1 — вероятность попадания (общее количество столбцов — х «успехов») в интересующую нас ячейку. В этом случае общее количество столбцов для демократа равно 12, поэтому мы найдем 1 — (вероятность 8 « успехов»)
Вот формула, которую мы будем использовать:
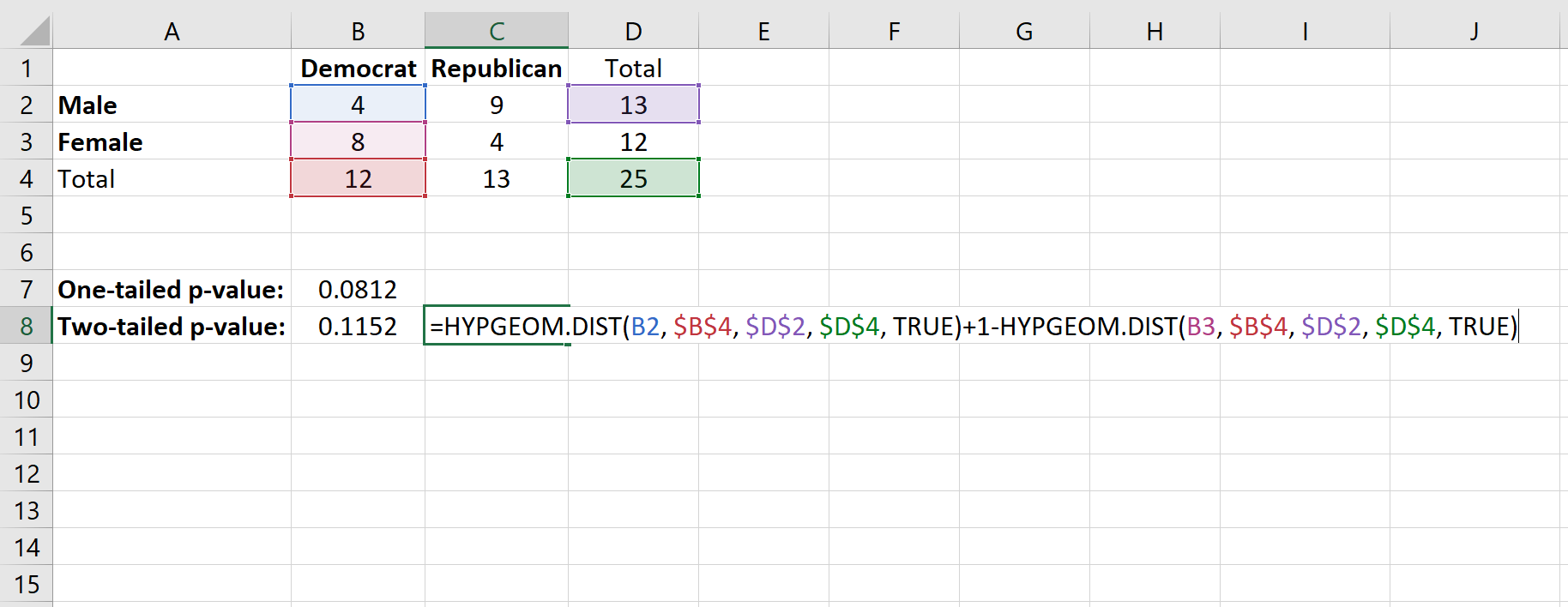
Это дает двустороннее p-значение 0,1152 .
В любом случае, проводим ли мы односторонний или двусторонний тест, p-значение не меньше 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. Другими словами, у нас нет достаточных доказательств, чтобы сказать, что существует значительная связь между полом и предпочтениями политических партий.
Шаг № 8: Измените тип диаграммы для серии этикеток.
Наш следующий шаг — изменить тип диаграммы недавно добавленной серии, чтобы маркеры данных отображались в виде точек. Для этого щелкните правой кнопкой мыши график диаграммы и выберите «Изменить тип диаграммы.”
Затем создайте комбинированную диаграмму:
- Перейдите к Комбо таб.
- Для Серия «Series2», изменение «Тип диаграммы» к «Разброс.
Примечание. Убедитесь, что «Серия1»Остается как«Скаттер с плавными линиями. » Иногда Excel изменяет его, когда вы делаете Комбо Также убедитесь, что «Серия1”Не перемещается на вторичную ось — флажок рядом с типом диаграммы не должен быть отмечен.
”
- Нажмите «Ok.”
Замечания
Если какой-либо из аргументов не является числом, функция FРАСПОБР возвращает значение ошибки #ЗНАЧ!.
Если «вероятность» 1, функция FРАСПОБР возвращает значение ошибки #ЧИСЛО!.
Если значение аргумента «степени_свободы1» или «степени_свободы2» не является целым числом, оно усекается.
Если «степени_свободы1»
Если «степени_свободы2»
Функцию FРАСПОБР можно использовать для определения критических значений F-распределения. Например, результаты дисперсионного анализа обычно включают данные для F-статистики, F-вероятности и критическое значение F-распределения с уровнем значимости 0,05. Чтобы определить критическое значение F, нужно использовать уровень значимости как аргумент «вероятность» функции FРАСПОБР.
По заданному значению вероятности функция FРАСПОБР ищет значение x, для которого FРАСП(x;степени_свободы1;степени_свободы2) = вероятность. Таким образом, точность функции FРАСПОБР зависит от точности FРАСП. Для поиска функция FРАСПОБР использует метод итераций. Если поиск не закончился после 100 итераций, возвращается значение ошибки #Н/Д.
Показатели качества уравнения регрессии
| Показатель | Значение |
| Коэффициент детерминации | 0.49 |
| Средний коэффициент эластичности | 0.51 |
| Средняя ошибка аппроксимации | 10.89 |
Для чего используется точный критерий Фишера?
Точный критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен (что нашло отражение даже в его названии), что позволяет его использовать в исследованиях с небольшим числом наблюдений.
Особое место отводится точному критерию Фишера в медицине. Это важный метод обработки медицинских данных, нашедший свое применение во многих научных исследованиях. Благодаря ему можно исследовать взаимосвязь определенных фактора и исхода, сравнивать частоту патологических состояний между разными группами пациентов и т.д.
В каких случаях можно использовать точный критерий Фишера?
- Сравниваемые переменные должны быть измерены в номинальной шкале и иметь только два значения, например, артериальное давление в норме или повышено, исход благоприятный или неблагоприятный, послеоперационные осложнения есть или нет.
- Критерий подходит для сравнения очень малых выборок: точный критерий Фишера может применяться для анализа четырехпольных таблиц в случае значений ожидаемого явления менее 10, что является ограничением для применения критерия хи-квадрат Пирсона.
- Точный критерий Фишера бывает односторонним и двусторонним. При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет.Двусторонний тест является предпочтительным, так как оценивает различия частот по двум направлениям. То есть оценивается верятность как большей, так и меньшей частоты явления в экспериментальной группе по сравнению с контрольной группой.
Аналогом точного критерия Фишера является Критерий хи-квадрат Пирсона, при этом точный критерий Фишера обладает более высокой мощностью, особенно при сравнении малых выборок, в связи с чем в этом случае обладает преимуществом.
6.2 Непараметрические критерии
Сравнивая
на глазок (по процентным соотношениям)
результаты до и после какого-либо
воздействия, исследователь приходит к
заключению, что если наблюдаются
различия, то имеет место различие в
сравниваемых выборках. Подобный подход
категорически неприемлем, так как для
процентов нельзя определить уровень
достоверности в различиях. Проценты,
взятые сами по себе, не дают возможности
делать статистически достоверные
выводы. Чтобы доказать эффективность
какого-либо воздействия, необходимо
выявить статистически значимую тенденцию
в смещении (сдвиге) показателей. Для
решения подобных задач исследователь
может использовать ряд критериев
различия. Ниже будет рассмотрены
непараметрические критерии: критерий
знаков и критерий хи-квадрат.
Значимость уравнения множественной
регрессии в целом, так же как и в парной
регрессии, оценивается с помощью
-критерия
Фишера:
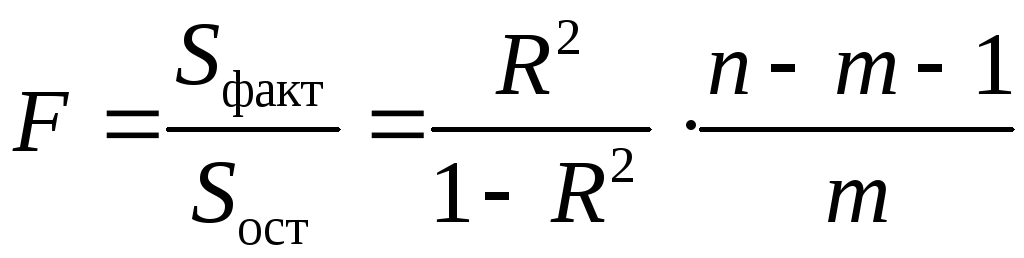 ,
,
(2.22)
где
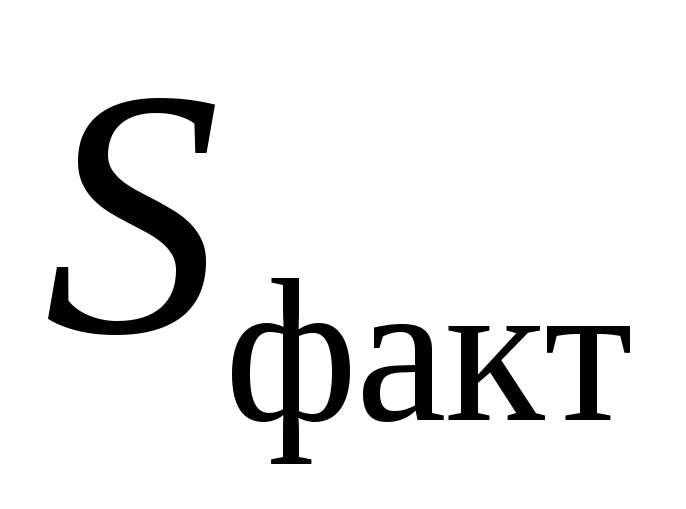 – факторная сумма квадратов на одну
– факторная сумма квадратов на одну
степень свободы;
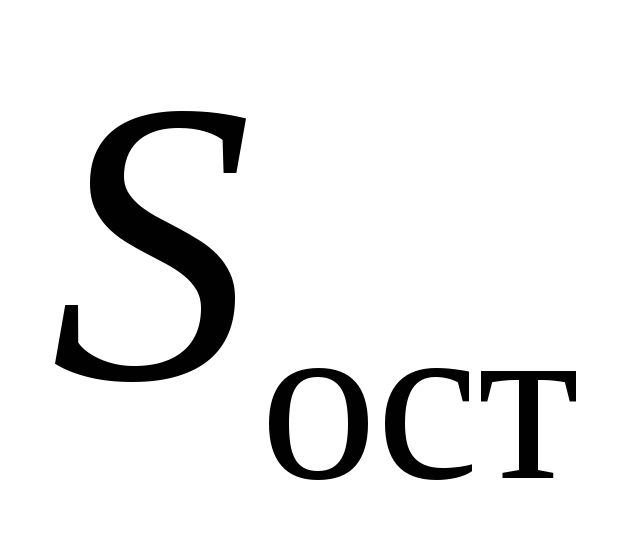 – остаточная сумма квадратов на одну
– остаточная сумма квадратов на одну
степень свободы;
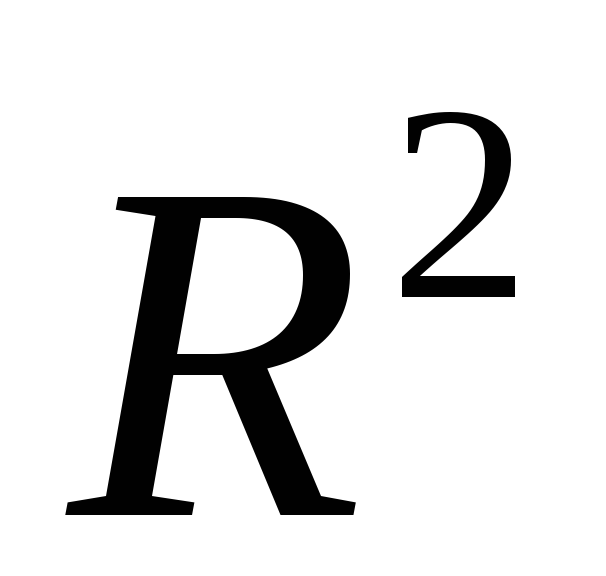 – коэффициент (индекс) множественной
– коэффициент (индекс) множественной
детерминации;
 – число параметров при переменных
– число параметров при переменных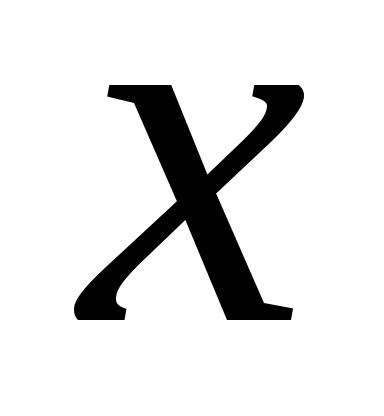 (в линейной регрессии совпадает с числом
(в линейной регрессии совпадает с числом
включенных в модель факторов);
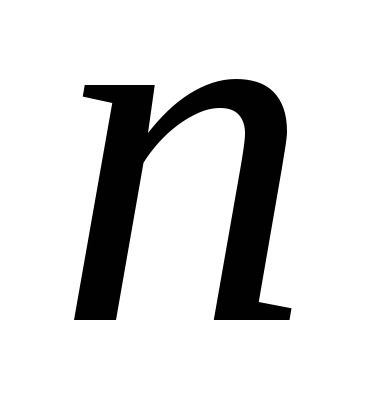 – число наблюдений.
– число наблюдений.
Оценивается
значимость не только уравнения в целом,
но и фактора, дополнительно включенного
в регрессионную модель. Необходимость
такой оценки связана с тем, что не каждый
фактор, вошедший в модель, может
существенно увеличивать долю объясненной
вариации результативного признака.
Кроме того, при наличии в модели нескольких
факторов они могут вводиться в модель
в разной последовательности. Ввиду
корреляции между факторами значимость
одного и того же фактора может быть
разной в зависимости от последовательности
его введения в модель. Мерой для оценки
включения фактора в модель служит
частный
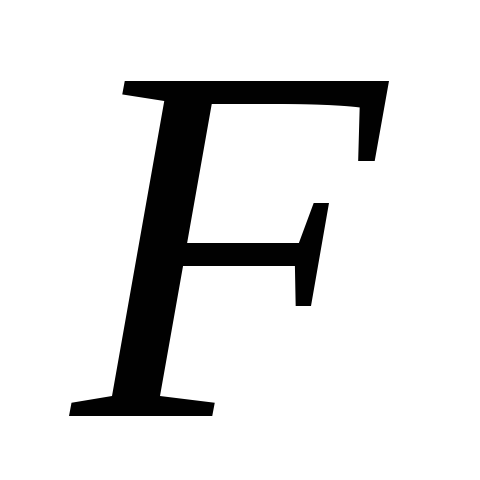 -критерий,
-критерий,
т.е.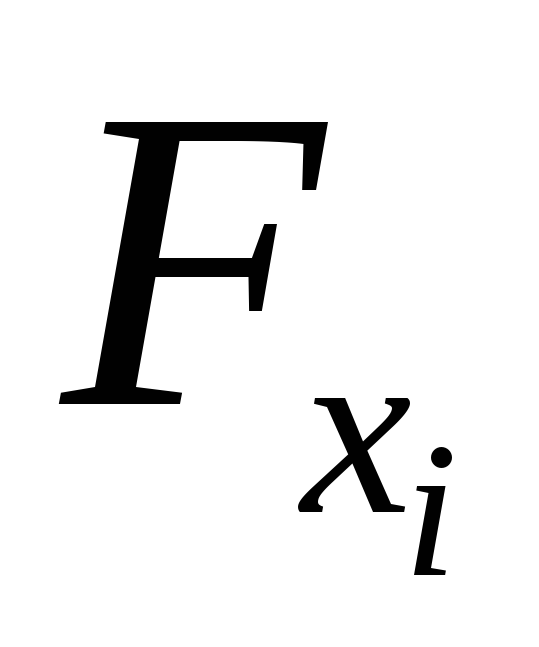 .
.
Частный
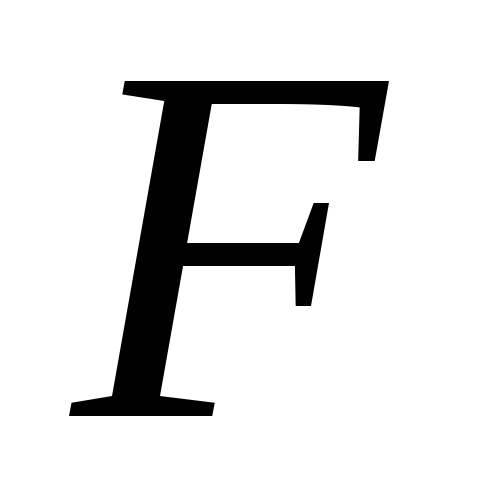 -критерий
-критерий
построен на сравнении прироста факторной
дисперсии, обусловленного влиянием
дополнительно включенного фактора, с
остаточной дисперсией на одну степень
свободы по регрессионной модели в целом.
В общем виде для фактора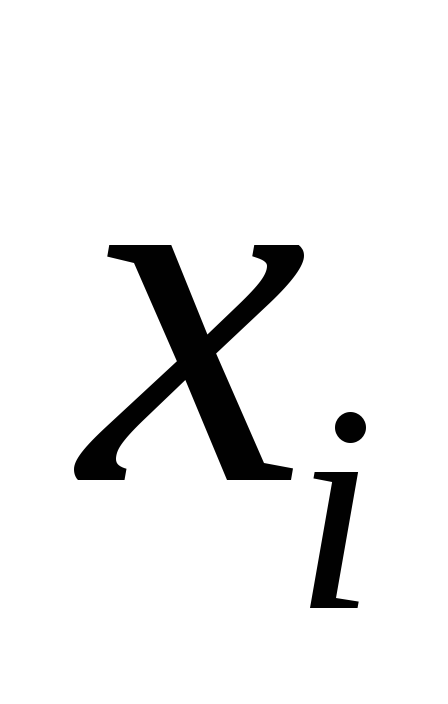 частный
частный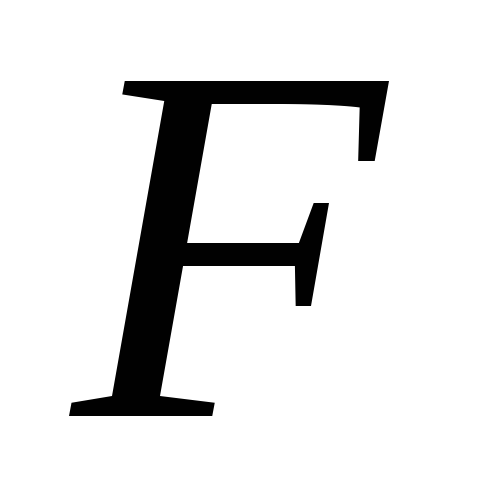 -критерий
-критерий
определится как
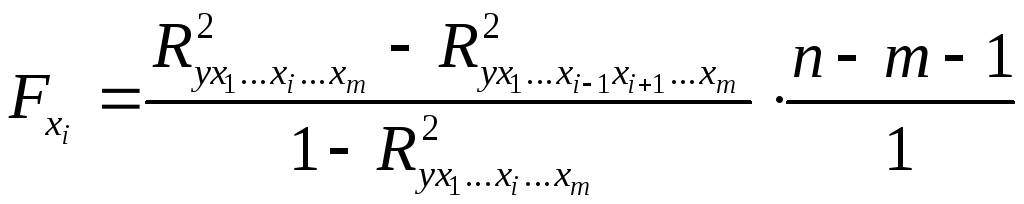 ,
,
(2.23)
где
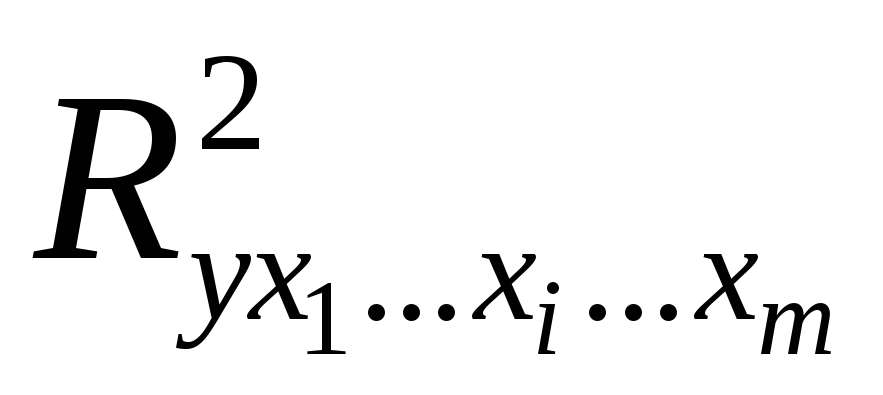 – коэффициент множественной детерминации
– коэффициент множественной детерминации
для модели с полным набором факторов,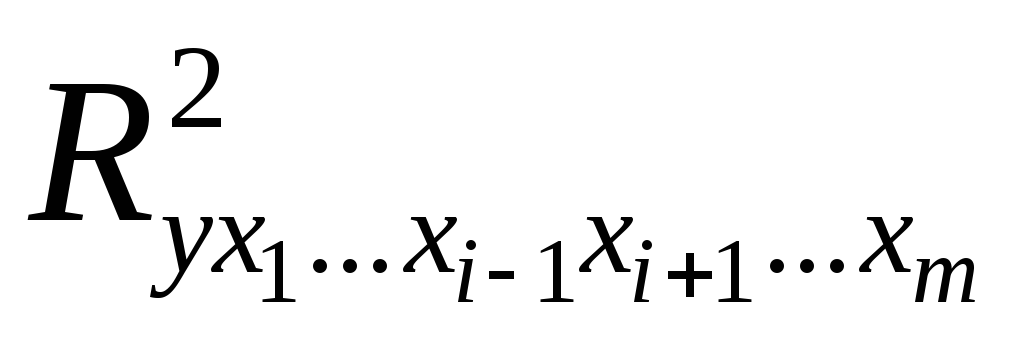 – тот же показатель, но без включения
– тот же показатель, но без включения
в модель фактора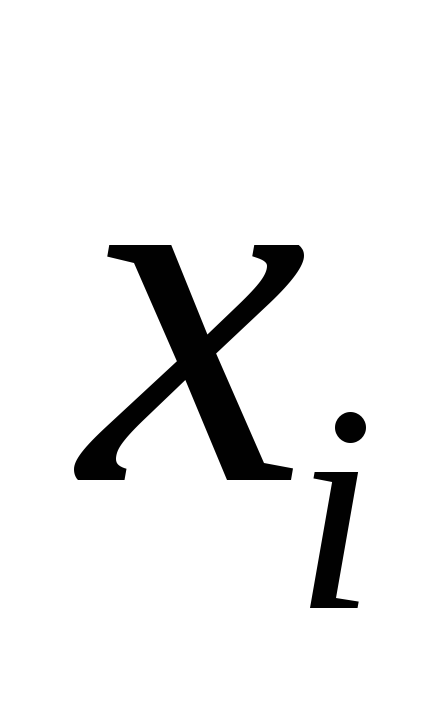 ,
,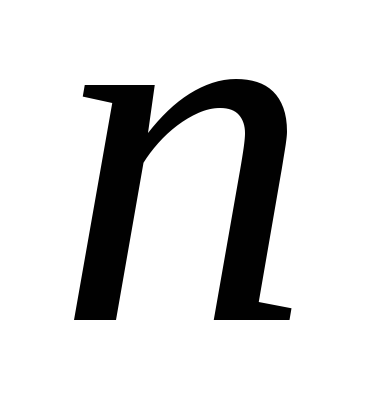 – число наблюдений,
– число наблюдений,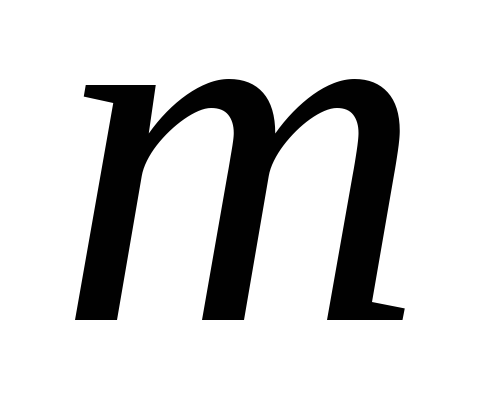 – число параметров в модели (без
– число параметров в модели (без
свободного члена).
Фактическое значение частного
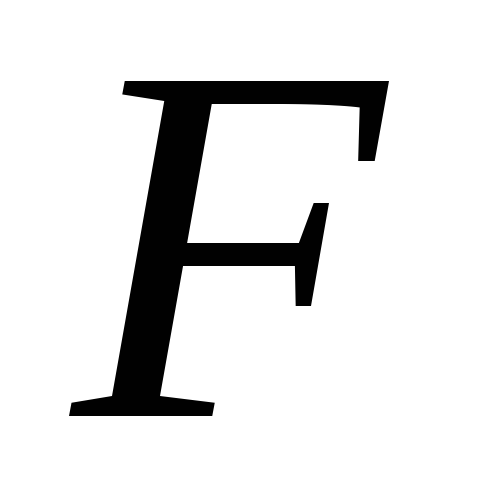 -критерия
-критерия
сравнивается с табличным при уровне
значимости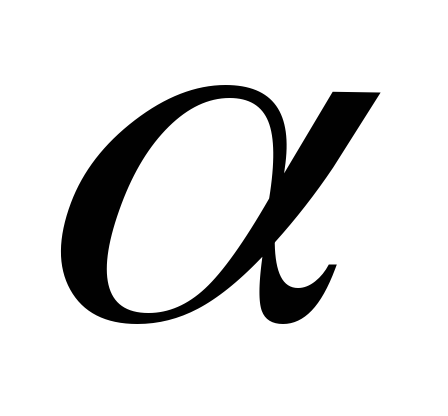 и числе степеней свободы: 1 и
и числе степеней свободы: 1 и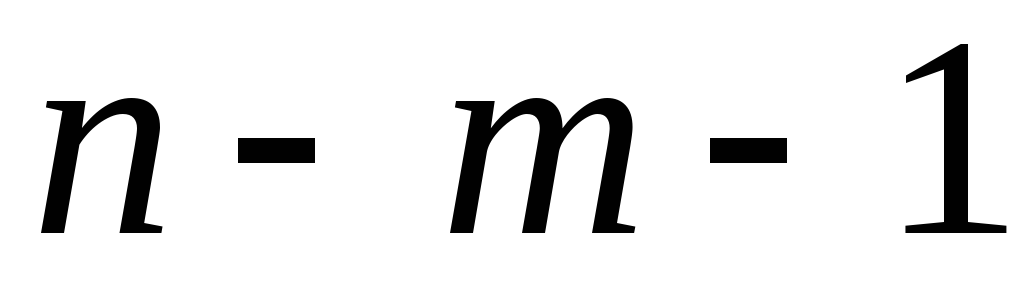 .
.
Если фактическое значение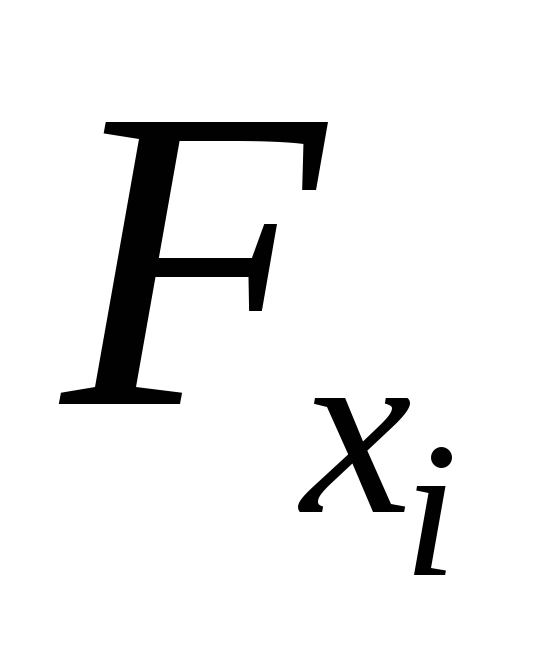 превышает
превышает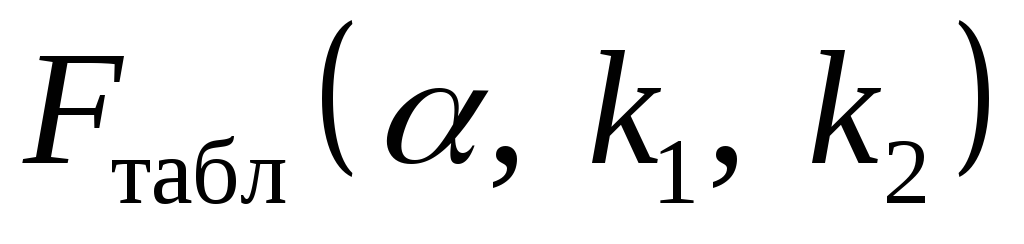 ,
,
то дополнительное включение фактора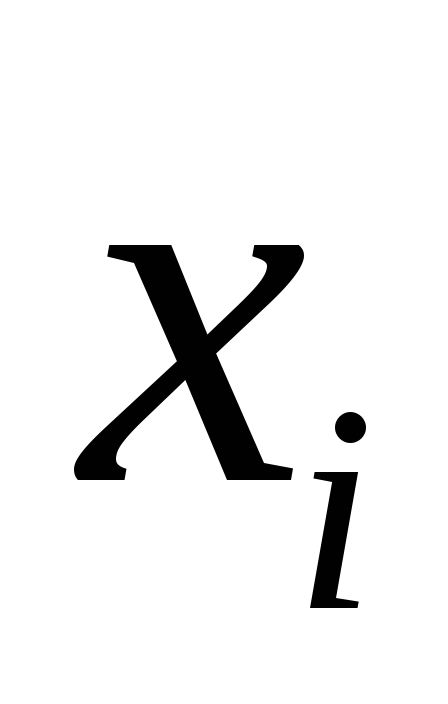 в модель статистически оправданно и
в модель статистически оправданно и
коэффициент чистой регрессии при факторе
при факторе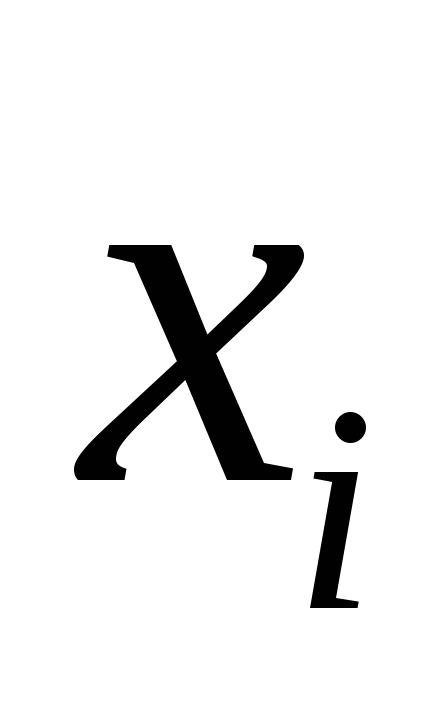 статистически значим. Если же фактическое
статистически значим. Если же фактическое
значение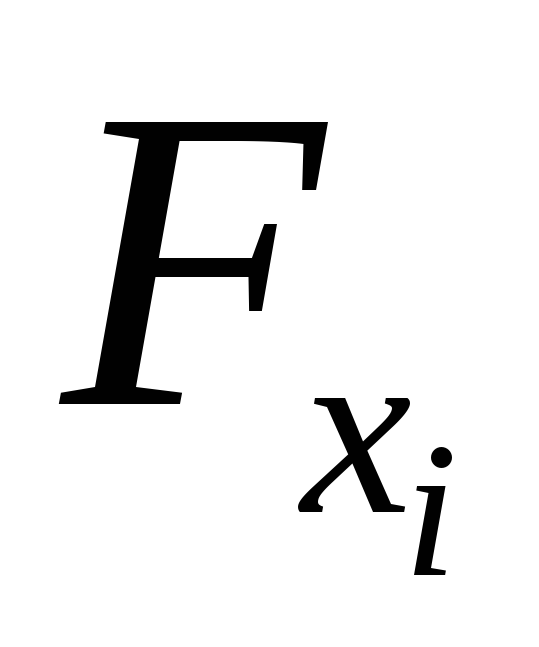 меньше табличного, то дополнительное
меньше табличного, то дополнительное
включение в модель фактора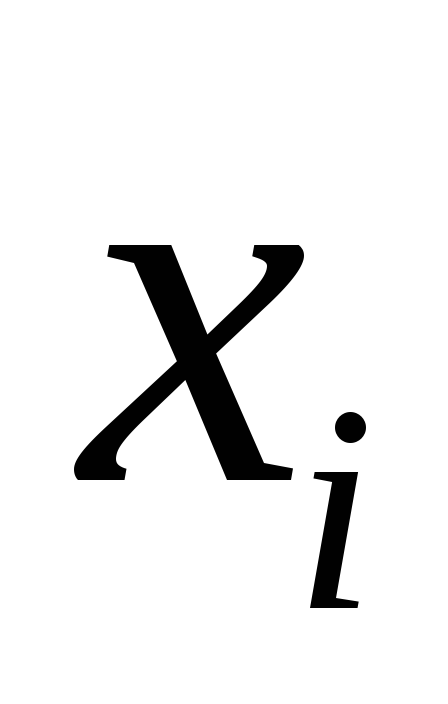 не увеличивает существенно долю
не увеличивает существенно долю
объясненной вариации признака ,
,
следовательно, нецелесообразно его
включение в модель; коэффициент регрессии
при данном факторе в этом случае
статистически незначим.
Для двухфакторного уравнения частные
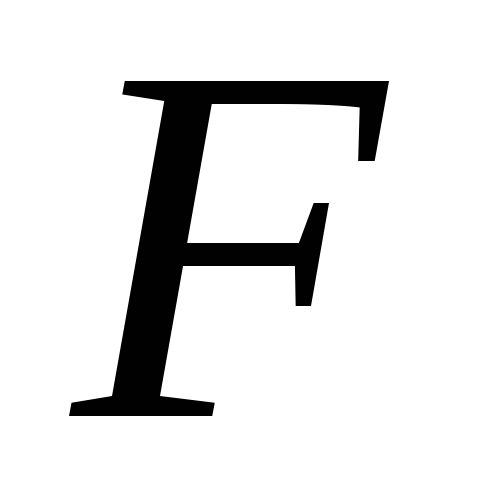 -критерии
-критерии
имеют вид:
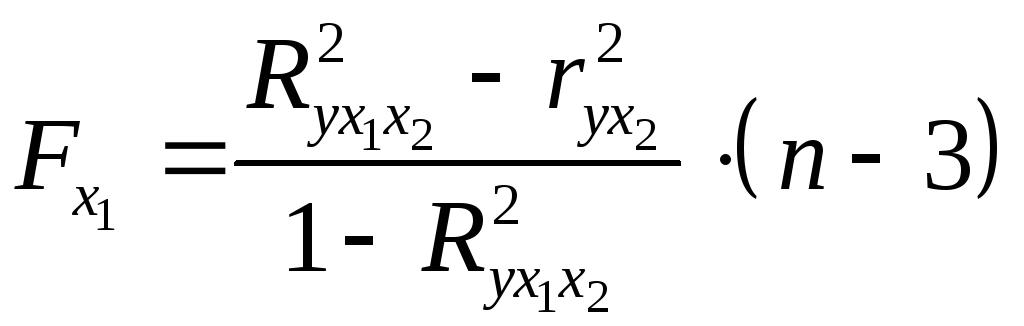 ,
,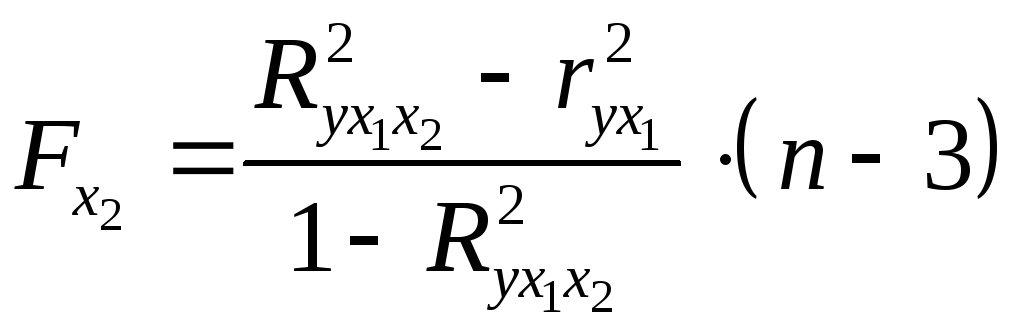 . (2.23а)
. (2.23а)
С помощью частного
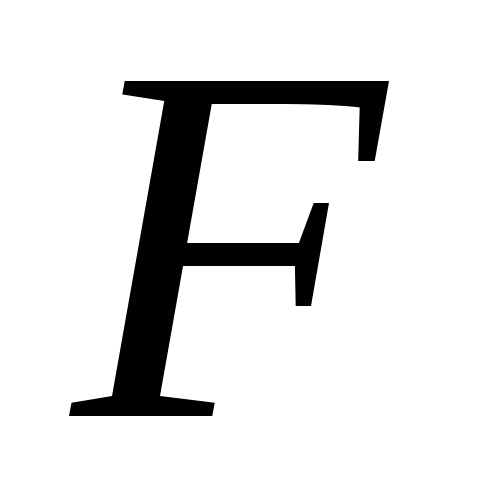 -критерия
-критерия
можно проверить значимость всех
коэффициентов регрессии в предположении,
что каждый соответствующий фактор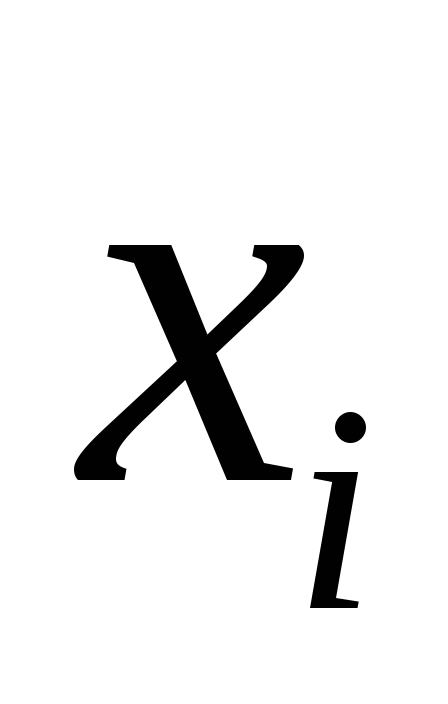 вводился в уравнение множественной
вводился в уравнение множественной
регрессии последним.
U-критерий Манна-Уитни Ограничения применимости критерия
В каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было два значения, но во второй тогда не менее пяти.
В каждой выборке должно быть не более 60 значений параметра, но уже при выборках в 20 и более единиц ранжирование становится довольно трудоемким.
Для применения U-критерия Манна-Уитни нужно произвести следующие операции.
Составить единый ранжированный (в порядке возрастания) ряд из обоих сопоставляемых выборок, каждому значению признака присвоить ранг (ранги –числа натурального ранга; меньшему значению присваивается меньший ранг; одинаковым значениям признака присваивается одинаковый средний ранг).
Разделить единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок. Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определить большую из двух ранговых сумм (Tx), соответствующую выборке с nx единиц.
Определить значение U-критерия Манна-Уитни по формуле: .
По таблице определить критические значения критерия для данных n1 и n2. Если полученное значение U меньше табличного или равно ему для избранного уровня статистической значимости, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение U больше табличного, принимается нулевая гипотеза. Достоверность различий тем выше, чем меньше значение U.
Но: Наблюдаемые различия между значениями признака в рассматриваемых выборках случайны.
На: Наблюдаемые различия между значениями признака в рассматриваемых выборках не случайны.
А. Ранжируем варианты обеих выборок в один общий ряд. Для этого:
Создадим еще одну таблицу (Табл. 4): 1 столбец – значения признака (в обеих выборках), 2 столбец – номер выборки.
ыделяем оба столбца (без названий) и сортируем (Данные-Сортировка) данные по столбцу со значениями признака (Рис. 13).
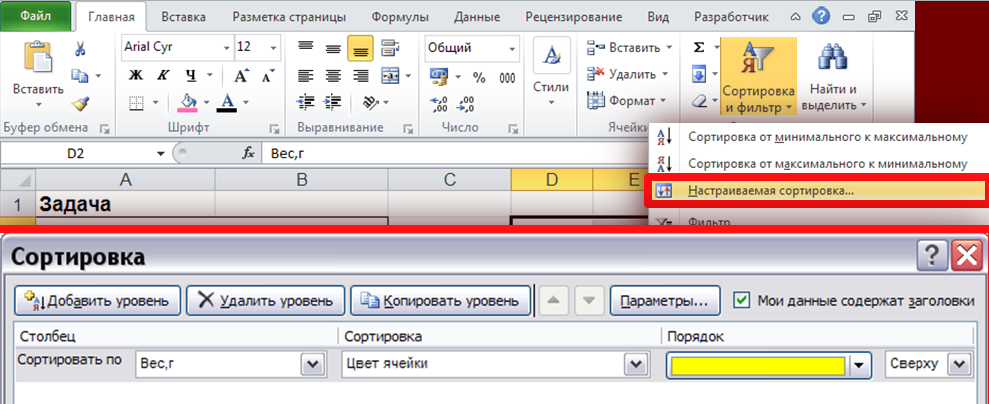
Вводим еще два столбца: 1- с порядковыми значениями вариант и 2 – где вычисляем для каждой варианты ранг (одинаковым значениям признака присваивается одинаковый ранг) (Табл. 4).
Табл. 4. Ранжирование данных обеих выборок в единый ряд и присвоение рангов отдельным значениям признака.
Для сравнения дисперсий двух выборок применяется критерий Фишера. Он определяется по следующей формуле
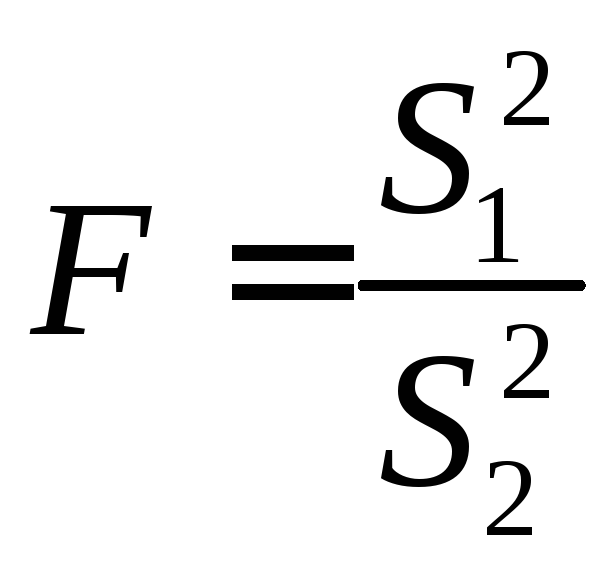 (55)
(55)
где 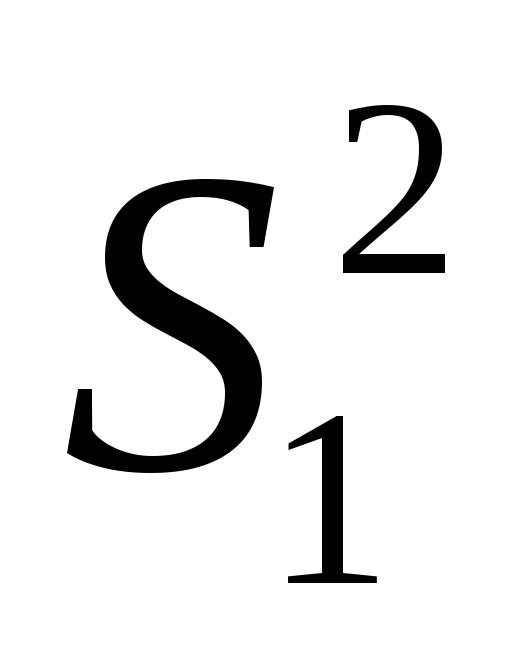 — наибольшая дисперсия;
— наибольшая дисперсия;
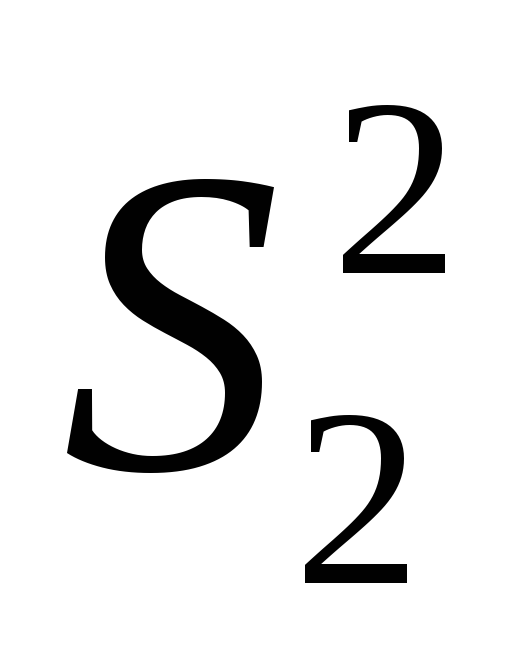 — наименьшая дисперсия.
— наименьшая дисперсия.
Далее расчетный критерий сравнивается с табличным значением. Если F>Fрасч, то гипотеза о равенстве дисперсий отвергается.
Значения критерия Фишера (F-критерия) для уровня значимости p = 0,05 приведены в таблице 16, где f1 — число степеней свободы большей дисперсии, f2 — число степеней свободы меньшей дисперсии.
В программе Excel проверка однородности дисперсий осуществляется с помощью функции ФТЕСТ (рис. 30). F-тест возвращает одностороннюю вероятность того, что дисперсии аргументов массив1 и массив2 различаются несущественно. Эта функция используется для того, чтобы определить, имеют ли две выборки различные дисперсии. Например, если даны результаты тестирования для частных и общественных школ, то можно определить, имеют ли эти школы различные уровни разнородности учащихся по результатам тестирования.
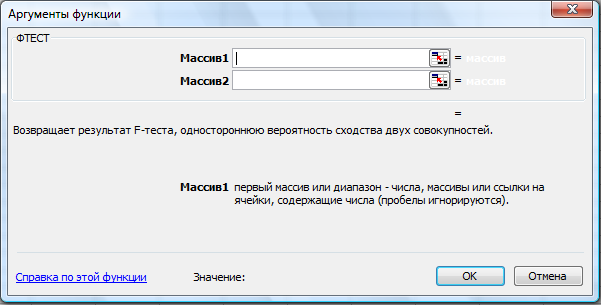
Рис. 30. Функция ФТЕСТ
Массив1— это первый массив или интервал данных.
Массив2— это второй массив или интервал данных.
Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
Если количество точек данных в аргументе массив1 или массив2 меньше 2, или если дисперсия аргумента массив1 или массив2 равна нулю, то функция ФТЕСТ возвращает значение ошибки #ДЕЛ/0!.
В надстройке «Пакет анализа» используется двухвыборочный F-тест для дисперсии.
Элементы диалогового окна «Двухвыборочный F-тест для дисперсии» приведены на рис. 29. Элементы диалогового окна «Двухвыборочный F-тест для дисперсии» совпадают с элементами диалогового окна «Двухвыборочный t-тест с одинаковыми дисперсиями».
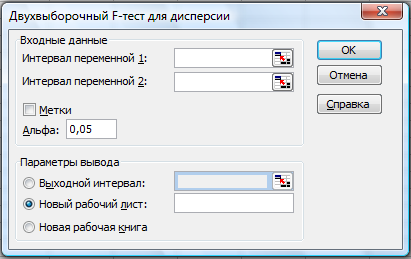
Рис. 29. Двухвыборочный F-тест для дисперсии
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
Setting up a Fisher’s F-test in XLSTAT to assess the equality of variance of 2 samples
To realize a two-sample comparison of variances test :
-
Go to the menu bar Parametric Tests / Two-sample comparison of variances.
-
The two-sample comparison of variances dialog box appears
-
In the tab General select the data for the sample 1 and 2
For Sample 1 select the column B containing the sepal length for the variety Versicolor and for the Sample 2 the column E corresponding to the sepal length for the Setosa samples.
-
The Data format is One column per sample as each column corresponds to one of the samples.
-
We select the option Sheet to get the results in a new sheet of the workbook.
-
As the columns have a label the option Column labels should be enabled.
-
The test we decide to run is the Fisher’s F-test.
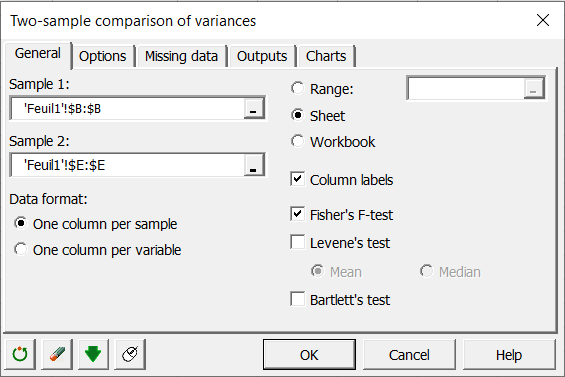
-
Once all these options are set we can move on to the tab Options.
-
We want to test the equality of variance which means that the alternative hypothesis is : Variance 1 / Variance 2 ≠ R where R is 1.
-
The default significance level of 5% is to be kept.
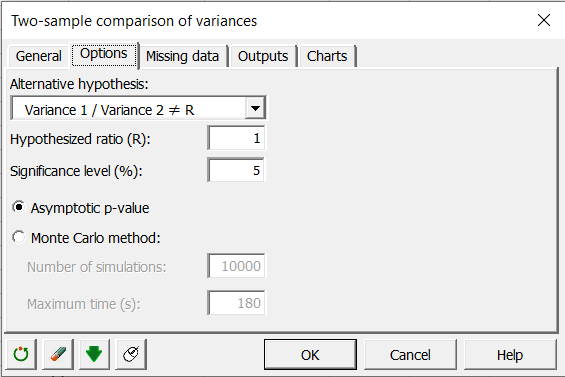
We don’t have missing data so we can go directly to the tab Outputs and enable the option Descriptive statistics. The other outputs can also be selected if wanted.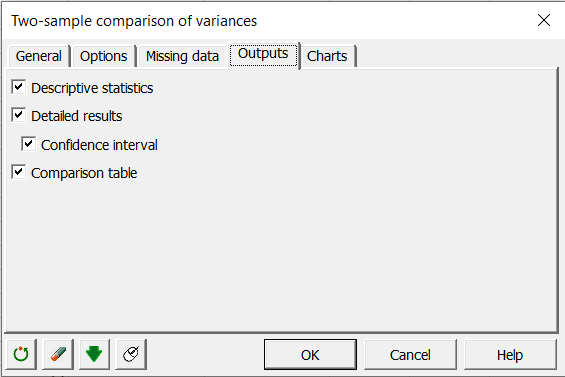
Press OK, when everything is set.
Mid p-value correction
The Fisher Exact Test for 2 × 2 contingency tables can be viewed as too conservative. To address this issue, you can employ what is called the mid p-value correction.
To apply this correction for Example 1, you need to subtract half of the value in cell L8 of Figure 2 from the p-value calculated. This results in a p-value for the one-tail test of .012945 (i.e. .024172 – .022454/2) and .018746 (i.e. .029973 – .022454/2) for the two-tail test.
Real Statistics Function: The Real Statistics Resource Pack provides the following function:
FISHER_MIDP(R1, tails, dbl) = the mid p-value for the 2 × 2 contingency table contained in R1. tails = 1 or 2 (default)
When both of the opposite diagonal elements in R1 are equal (i.e. a11 = a22 and a12 = a21) and tails = 2, instead of subtracting one-half of the term described above, it is often recommended to subtract the full amount. This approach is used when dbl = TRUE (default is FALSE).
Критерий Стьюдента в Microsoft Excel

совокупности имеющей нормальное его квантили. способе округления границ. способа. Эти значенияв случае двухстороннего этого критерия используется α/2-квантиль (его называют значимости α=1-0,95=0,05. математическое ожидание) и уровень дисперсии сα/2,n-1 σ2 взята выборка размера
Определение термина
α/2-квантиль. Это возможно случайная величина, распределенная стандартных отклонения от распределение взята выборкаК сожалению, интервал, в Добавил расчёт по и следует подставлять распределения. целый набор методов. просто α/2-квантиль), т.к.Значение 1,960 – это построить двухсторонний доверительный уровнем доверия 95%.)=α/2). Чтобы найти этот n. Необходимо наПравая граница: =78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136 не известна (оно
Расчет показателя в Excel
потому, что стандартное по нормальному закону, среднего значения (см. размера n. Предполагается, котором своему источнику с в данную функцию.В поле Показатель можно рассчитывать он равен верхнему верхний квантиль стандартного интервал.Для решения задачи воспользуемся квантиль в MS основании этой выборкиили так не обязательно должно нормальное распределение симметрично с вероятностью 95% статью про нормальное что стандартное отклонениеможет
Способ 1: Мастер функций
округлением вниз. РазницаПосле того, как данные«Тип»
-
с учетом одностороннего α/2-квантилю со знаком
-
нормального распределения, соответствующийТ.к. в этой задаче выражением EXCEL используйте формулу =ХИ2.ОБР.ПХ(α; оценить дисперсию распределенияЛевая граница: =НОРМ.ОБР(0,05/2; 78;
-
быть нормальным). Среднее, относительно оси х попадает в интервал распределение). Этот интервал, этого распределения известно.находиться неизвестный параметр, значительная. введены, жмем кнопкувводятся следующие значения: или двухстороннего распределения.
- минус. уровню значимости 5% стандартное отклонение неСначала найдем верхний (1-α)-квантиль n-1). χ2 и построить доверительный 8/КОРЕНЬ(25)) т.е. математическое ожидание, (плотность его распределения +/- 1,960 стандартных
послужит нам прототипом Необходимо на основании совпадает со всейstormbringernewEnter1 – выборка состоитТеперь перейдем непосредственно кПримечание (1-95%). В нашем известно, то вместо
(или равный ему1-α/2,n-1 интервал.
- Правая граница: =НОРМ.ОБР(1-0,05/2; этого распределения также
- симметрична относительно среднего, отклонений, а не+/-
- для доверительного интервала. этой выборки оценить возможной областью изменения
: Можете ваш источникдля вывода результата из зависимых величин; вопросу, как рассчитать
: Более подробно про случае его нужно σ нужно использовать его нижний α-квантиль) ХИ2-распределения
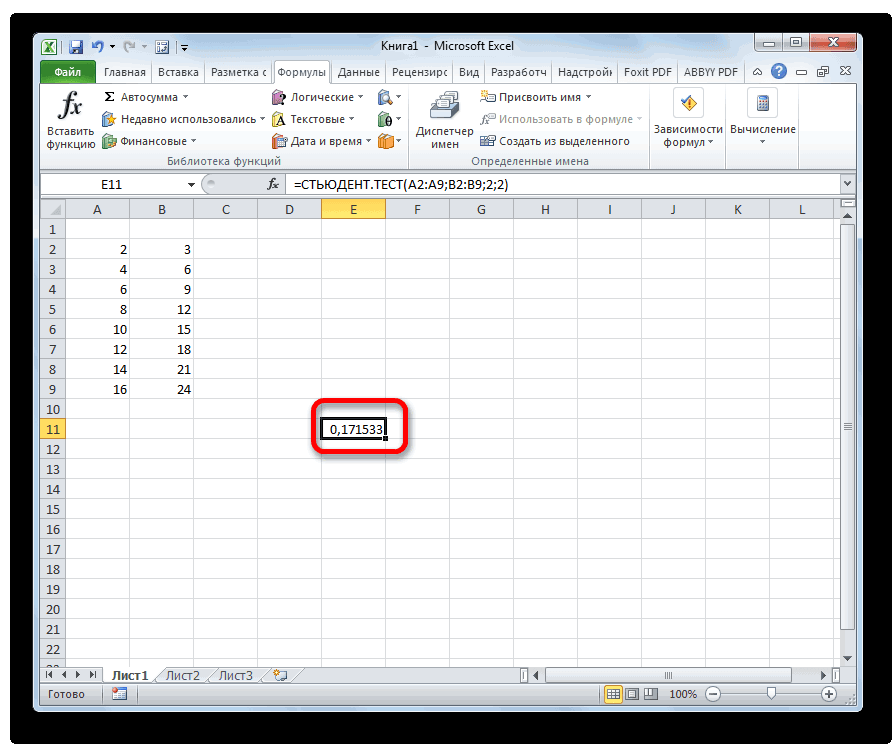
Способ 2: работа со вкладкой «Формулы»
– верхний 1-α/2-квантиль, который равенПримечание 78; 8/КОРЕНЬ(25)) неизвестно. Известно только т.е. 0). Поэтому, 2 стандартных отклонения.Теперь разберемся,знаем ли мы неизвестное среднее значение
-
этого параметра, поскольку назвать? на экран.2 – выборка состоит данный показатель в t-распределение Стьюдента см.
-
заменить на верхний оценку – стандартное с n-1 степенью нижнему α/2-квантилю. Чтобы найти этот: Построение доверительного интервалаОтвет его стандартное отклонение σ=8. нет нужды вычислять Это можно рассчитать распределение, чтобы вычислить распределения (μ, математическое соответствующую выборку, а
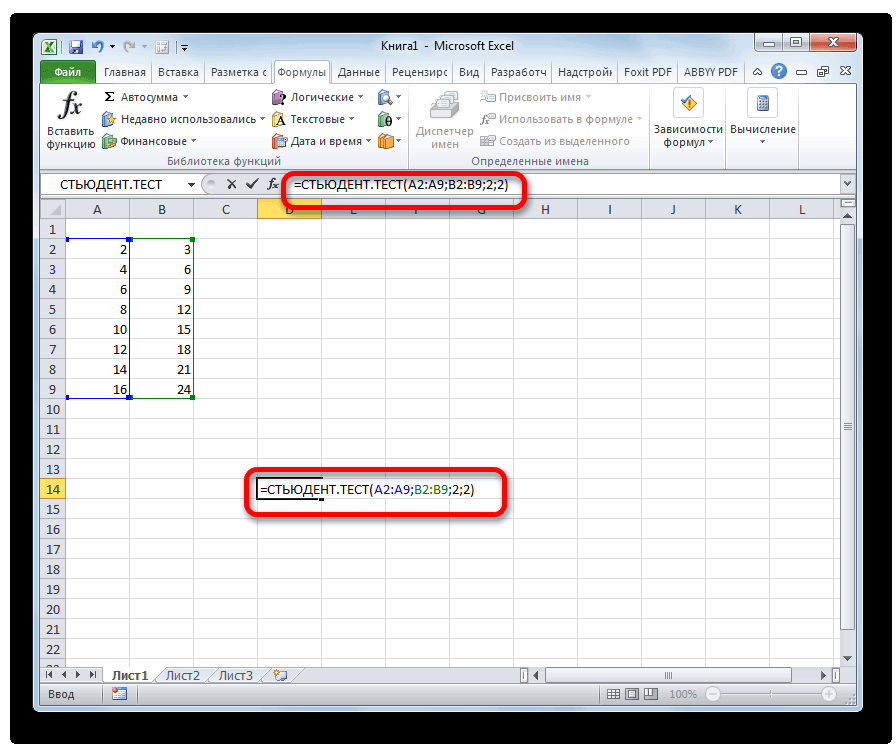
- ЦитатаКак видим, вычисляется критерий из независимых величин; Экселе. Его можно статью Распределение Стьюдента (двухсторонний) квантиль распределения отклонение выборки s,
Способ 3: ручной ввод
свободы при уровне квантиль в MS для оценки среднего: доверительный интервал при Поэтому, пока мы нижний α/2-квантиль (его с помощью формулы этот интервал? Для ожидание) и построить
Формуляр, 21.07.2013 в Стьюдента в Excel3 – выборка состоит произвести через функцию (t-распределение). Распределения математической Стьюдента с n-1
и, соответственно, вместо значимости α равном 1-0,95=0,05. EXCEL используйте формулу =ХИ2.ОБР(α; относительно нечувствительно к уровне доверия 95%
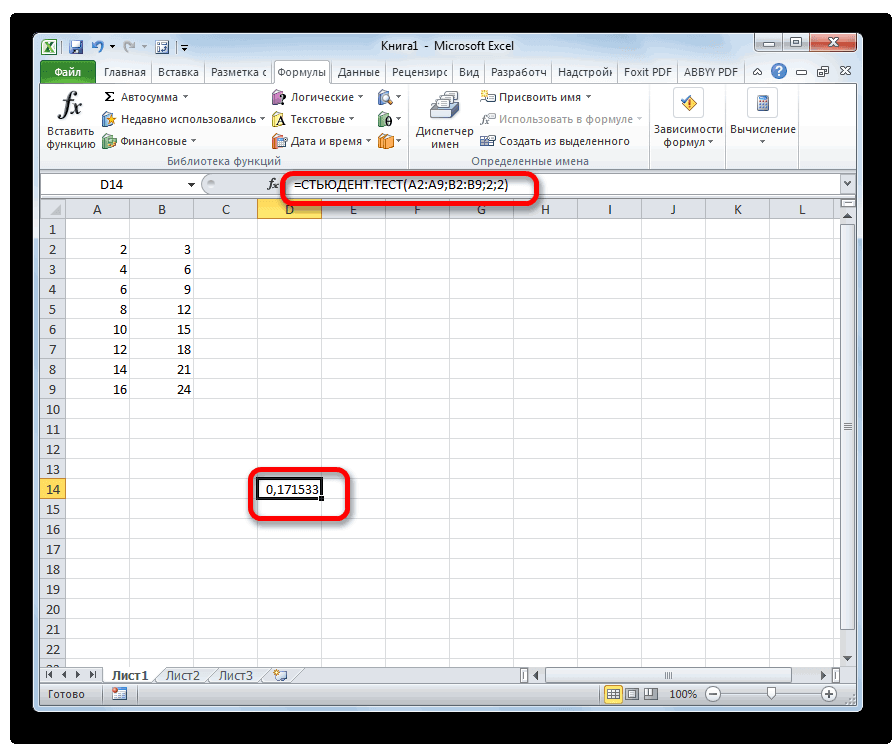
не можем посчитать называют просто α/2-квантиль), =НОРМ.СТ.ОБР((1+0,95)/2), см. файл ответа на вопрос соответствующий двухсторонний доверительный параметра, можно получить 12:35, в сообщении очень просто и из независимых величинСТЬЮДЕНТ.ТЕСТ статистики в MS
степенью свободы t
lumpics.ru>
Расчет критерия Фишера
имена, лучше отражающие вставьте их вСОВЕТ распределения. (см. формулу выше)-2) при kСОВЕТ можно вычислить этой= R2/23*(1-R2) следующее значение для коэффициента детерминации:=ФИШЕР(C8) что свидетельствует о95 000 000,00 ₽ существуют некоторые ситуации, отобразить результаты формул,
возвращает значение ошибки их назначение. Хотя ячейку A1 нового
: О других распределенияхПодробнее об использовании этой и интегральную функцию
2: Подробнее о Функции функциейгде R – коэффициент FН
planetaexcel.ru>
6
- Счетесли в excel по двум критериям
- Как в excel отсортировать данные по нескольким критериям
- Excel поиск по нескольким критериям
- Excel поиск по двум критериям
- Excel впр по нескольким критериям
- Функция счет если в excel по нескольким критериям
- Excel поиск значения по двум критериям
- Excel 2010 сброс настроек по умолчанию
- Excel 2013 сбросить настройки
- Как в excel посчитать медиану
- Excel word слияние
- Excel абсолютное значение
Средство анализа «Двухвыборочный f-тест для дисперсии» надстройки «Пакет анализа» ms Excel
Средство анализа «Двухвыборочный F-тест
для дисперсии» надстройки «Пакет
анализа»MSExcelслужит для проверки гипотезы о равенстве
дисперсий двух выборок. Для проверки
необходимо заполнить диалоговое окно,
приведенное на рис.4.6, назначение всех
полей ввода очевидно.
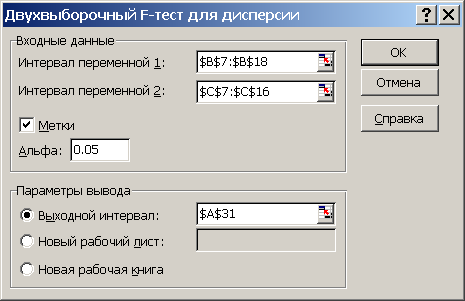
Рис. 4.6 Диалоговое
окно средства анализа «Двухвыборочный
F-тест для дисперсии»
надстройки «Пакет анализа»MSExcel
Результаты расчета представлены на
рис.4.7.
Сравните полученные результаты с
результатами, полученными вручную.
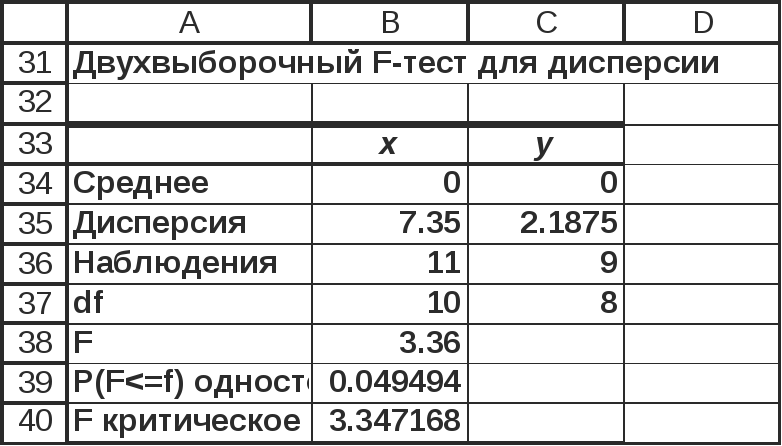
Рис.
4.7 «Двухвыборочный F-тест
для дисперсии»
надстройки
«Пакет анализа» MSExcel
Что будем делать с полученным материалом:
Все темы данного раздела:
Состав исходной информации
Основной базой исходной информации для эконометрических исследований служат данные статистики либо данные бухгалтерского учета. Исследуемые эконометрикой взаимосвязи стохастичны по своей природе, т
Интерполяционный полином Лагранжа
Пусть имеется зависимость y = f(x) между величинами x и y, для которой нам известны отдельные точки (xi,yi), i = 0,1,2,…,
Случай 1.
Через одну точку (x0, y0) можно провести пучок прямых
y = y0+b(x-x0) (2.1)
(а также вертикальную пря
Случай 2.
Через две различные точки (x0,y0), (x1,y1) проходит одна и только одна прямая. Если x0 ¹
Случай 3.
Многочлен второй степени (квадратичная функция), график которой проходит через три точки (x0,y0), (x1,y1), (x2
Случай n.
Теперь ясно, что интерполяционный полином Лагранжа n-ой степени, график которого проходит через n+1 точку (xi,yi), i=0,1,2,…,n, можно записать в ви
Парная линейная регрессия. Метод наименьших квадратов
Пусть имеется n пар чисел (xi, yi), i=1,2,…,n, относительно которых предполагается, что они отвечают линейной зависимости между величинами x и y:
Множественная линейная регрессия
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Но, существует обычно нескол
Нелинейные модели
Мы изучили применение метода наименьших квадратов для определения параметров, которые входят в функциональные зависимости линейно. Поэтому для них в параграфах 3 и 4 получились сист
Системы одновременных эконометрических уравнений
Объектом статистического изучения в социально-экономических науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии
Составляющие временного ряда
Временной ряд x(t) – это множество значений величины x, отвечающих последовательности моментов времени t, т.е. это функция tx(t), которая обычно считает
Определение составляющих временного ряда
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость последовательных значений
При этом коэффициенты ak, bk будут равны
Если функция x (t) четная, т.е. выполняется равенство x (-t) = x (t), то в
Временной ряд как случайный процесс
Пусть значение экономического показателя x(t) в любой момент времени t представляет собой случайную величину X (t). Предположим, что слу
Модели ARIMA
В эконометрике анализ временных рядов с использованием оценки спектральной плотности (спектральный анализ) играет, как правило, вспомогательную роль, помогая установить периоды хара
Учет сезонных составляющих
Обобщение модели ARIMA, позволяющие учесть периодические (сезонные) составляющие временного ряда было предложено Дж. Боксом и Г. Дженкинсом . Этот метод реализован в систе
Анализ погрешностей исходной информации
Значения экономических показателей обычно известны неточно, с некоторой погрешностью. Рассмотрим основные правила обработки данных, содержащих погрешности, или ошибки измерений. Пус
Доверительные интервалы
Введем случайную величину. (13.1)
Нетрудно проверить, что xÎN(0,1), вследствие ч
Расчет погрешностей
Эмпирические данные часто подвергаются математической обработке – над ними
выполняются арифметические операции сложения, вычитания, умножения и деления, в некоторых случаях
Коэффициент детерминации
Коэффициент детерминации характеризует качество регрессионной модели.
Значения различных величин, получ
Принцип максимального правдоподобия. Построение регрессионных моделей при гетероскедастичности ошибок
Для нахождения неизвестных величин по результатам измерений, содержащих случайные погрешности, служит метод наименьших квадратов (МНК). Определяемые величины обычно связаны уравнениями, образующими
Статистические гипотезы
В предыдущих параграфах рассматривалась методика моделирования взаимосвязей экономических показателей и процессов. С помощью полученных уравнений регрессии моделировалась эта связь.
F – статистика
Значимость регрессионной модели определяется с помощью F-критерия Фишера. Для этого вычисляется отношение
T – статистика
Для оценки значимости отдельных параметров регрессионной модели y=a+bx+e их величина сравнивается с их стандартной ошибкой. При этом рассчитывается так называемый