Диаграмма рассеяния в excel

Как рассчитать объединенную дисперсию в Excel (шаг за шагом)

В статистике объединенная дисперсия относится к среднему значению двух или более групповых дисперсий.

Мы используем слово «объединенные», чтобы указать, что мы «объединяем» две или более групповые дисперсии, чтобы получить единое число для общей дисперсии между группами.

На практике объединенная дисперсия чаще всего используется в двухвыборочном t-тесте , который используется для определения того, равны ли две средние значения совокупности.

Объединенная дисперсия между двумя выборками обычно обозначается как s p 2 и рассчитывается как:

s p 2 = ( (n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)

В этом руководстве представлен пошаговый пример того, как рассчитать объединенную дисперсию между двумя группами в Excel.

Во-первых, давайте создадим два набора данных:

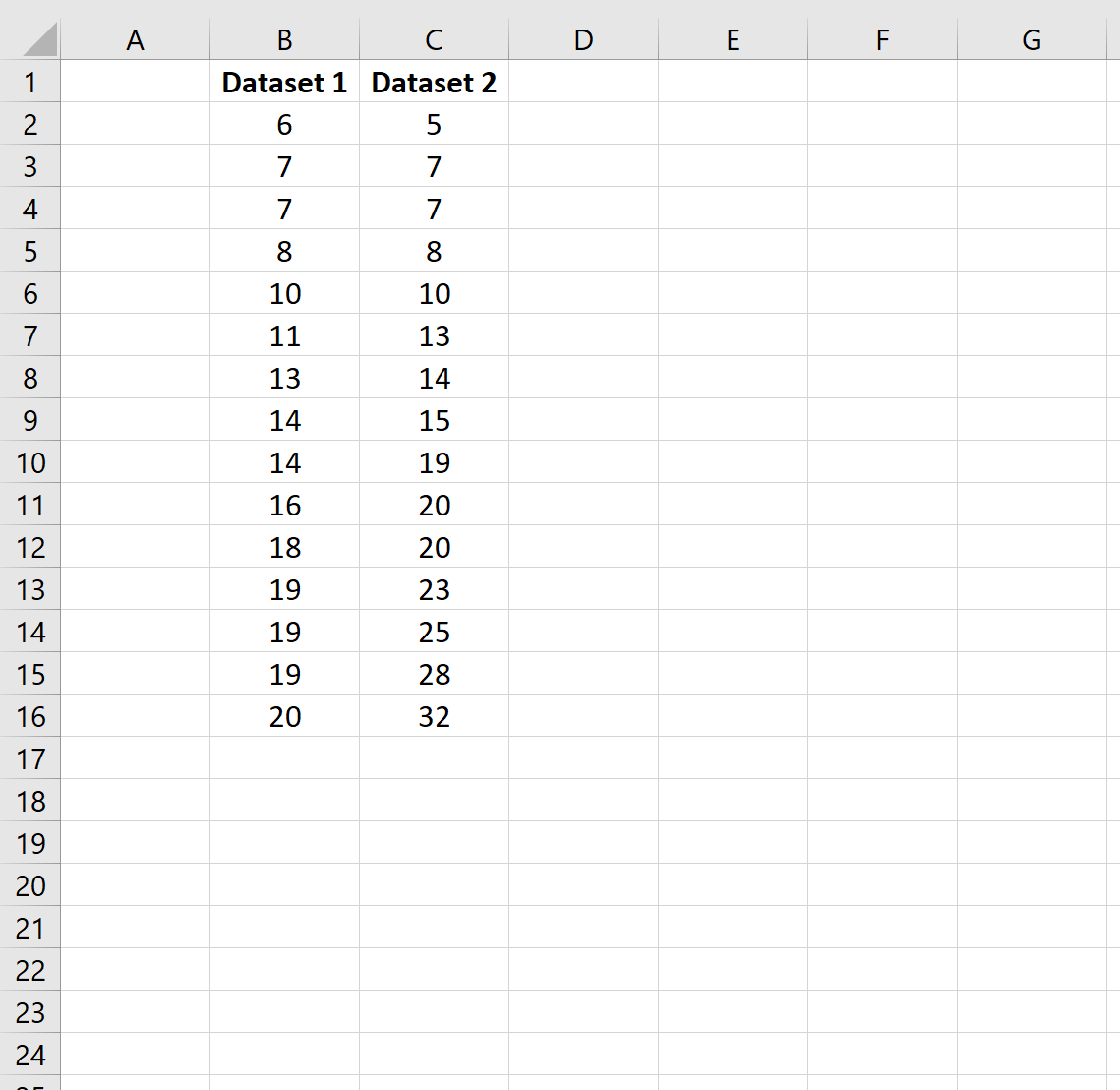
Шаг 2: Рассчитайте размер выборки и дисперсию выборки

Далее давайте рассчитаем размер выборки и дисперсию выборки для каждого набора данных.

В ячейках E17:F18 показаны формулы, которые мы использовали:

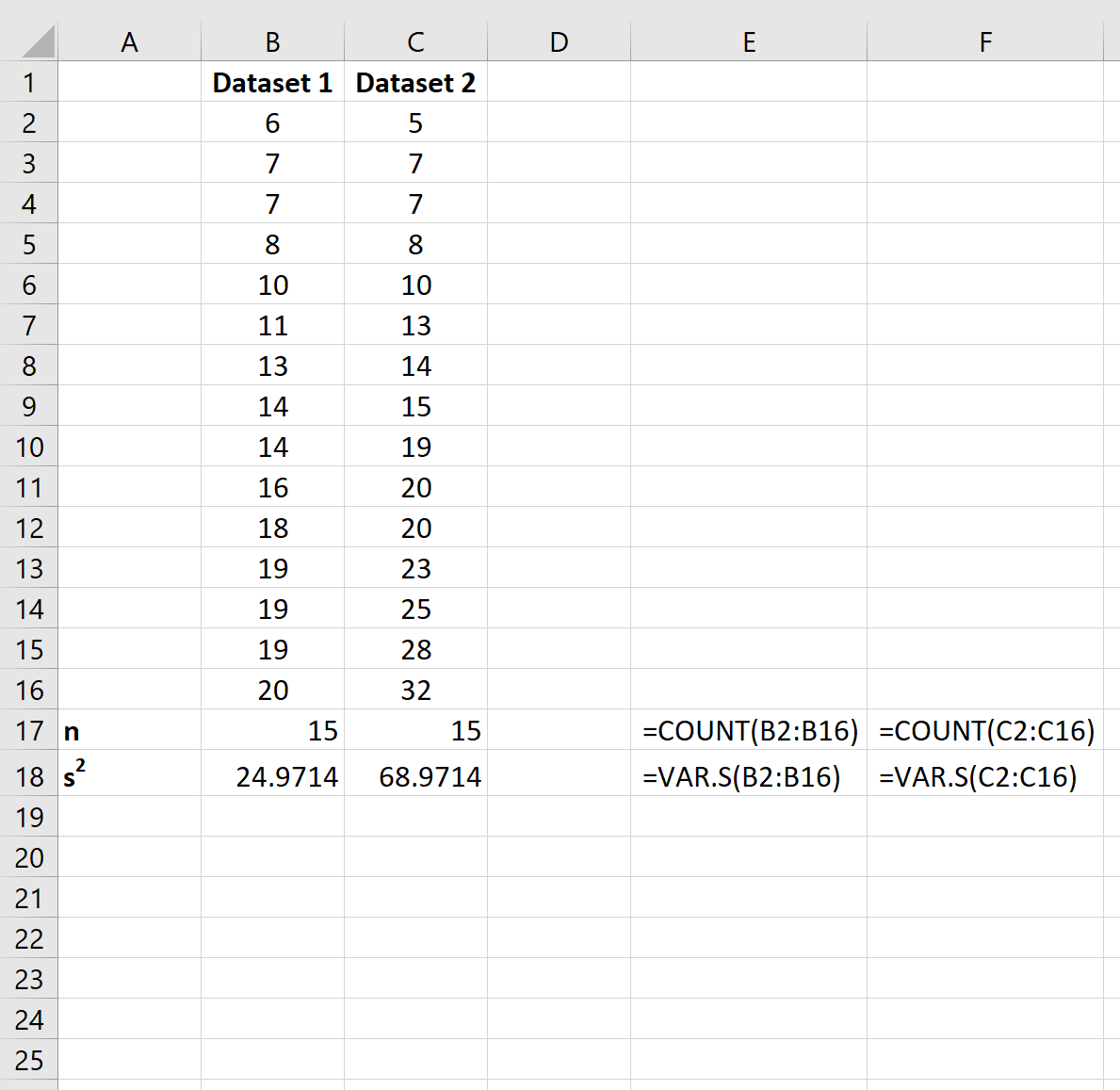
Шаг 3: Рассчитайте объединенную дисперсию

Наконец, мы можем использовать следующую формулу для расчета объединенной дисперсии:

Суммарная дисперсия между этими двумя группами оказывается равной 46,97 .

Бонус: вы можете использовать этот Калькулятор объединенной дисперсии для автоматического расчета объединенной дисперсии между двумя группами.

Источник

Пошаговое руководство по созданию точечной диаграммы с двумя наборами данных

Вот простое пошаговое руководство о том, как сделать точечную диаграмму с двумя наборами данных в Excel. Чтобы продолжить, вы должны открыть лист Excel с данными на вашем компьютере или вы можете открыть онлайн таблица Excel и вставьте туда данные.

1. Введите данные в две колонки в Excel. Первый столбец должен содержать значения независимой переменной, а второй столбец должен содержать значения зависимой переменной.
2. Выберите два столбца данных.
3. Перейдите в Вставить и нажмите Разброс значок диаграммы.
4. Выберите шаблон точечной диаграммы.
5. Нажмите на OK кнопку.
6. Точечная диаграмма будет вставлена ​​в ваш рабочий лист.
7. Чтобы добавить второй набор данных на точечную диаграмму, выполните следующие действия:
   • Нажмите на Дизайн диаграммы меню.
   • Нажмите на Выберите данные кнопку.
   • В  Выберите данные диалоговом окне нажмите на Добавить кнопку.
   • В  Серии диалоговом окне выберите диапазон ячеек для второго набора данных.
   • Нажмите на OK кнопку.
   • Нажмите на OK снова.

Вот и все, теперь у вас есть точечный график с двумя наборами данных! Ключ вводит каждый набор данных отдельно, а затем добавляет второй набор к существующей диаграмме.

Советы по созданию эффективных диаграмм рассеяния с двумя наборами данных

Чтобы получить максимальную отдачу от сравнения двух наборов данных на одном и том же точечном графике, помните об этих советах:

• Используйте разные цвета для каждого набора данных
• Добавьте описательные записи легенды, чтобы различать наборы данных
• Показать линии тренда для каждого набора данных, чтобы сделать корреляции четкими
• Отрегулируйте масштаб оси, чтобы распределить перекрывающиеся точки данных
• Избавьтесь от ненужного беспорядка, мешающего пониманию

Благодаря хорошо структурированной и настраиваемой диаграмме рассеяния с двумя наборами данных в Excel вы можете открыть совершенно новый уровень сравнения и анализа данных! Сопоставление делает очевидными сходства, различия и взаимодействие.

Дисперсия случайной величины

Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения .

Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E

Если случайная величина имеет дискретное распределение , то дисперсия вычисляется по формуле:

где x _i – значение, которое может принимать случайная величина, а μ – среднее значение ( математическое ожидание случайной величины ), р(x) – вероятность, что случайная величина примет значение х.

Если случайная величина имеет непрерывное распределение , то дисперсия вычисляется по формуле:

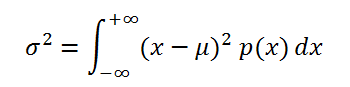
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.

Примечание : Дисперсия, является вторым центральным моментом , обозначается D, VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .

Примечание : О распределениях в MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .

Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .

Некоторые свойства дисперсии :

Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.

Var(Х)=E=E=E(X 2 )-E(2*X*E(X))+(E(X)) 2 =E(X 2 )-2*E(X)*E(X)+(E(X)) 2 =E(X 2 )-(E(X)) 2

Это свойство дисперсии используется в статье про линейную регрессию .

Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.

Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего .

Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних .

Примечание : квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).

Категоризованные диаграммы

Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые
категоризованные диаграммы
(coplot = conditioning plot).

Теперь вместо категориальной переменной
Режим
у нас имеется

непрерывная переменная
Давление
, которая принимает значения от 10 до 20. Предположим, что значение переменной
Давление
= 15, является неким пороговым и протекание процесса значительно отличается, если оно протекает при давлении от 10 до 15 и от 15 до 20. Используя этот факт строят 2 диаграммы:

• Пары значений (
  производительность; температура
  ) при давлении от 10 до 15:
• Пары значений (
  производительность; температура
  ) при давлении от 15 до 20.

Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.

Добавление настраиваемых полос ошибок в диаграммы Excel

Планки погрешностей, отличные от пользовательских планок погрешностей (т.е. фиксированные, процентные, стандартное отклонение и стандартная ошибка), применить довольно просто. Вам нужно просто выбрать вариант и указать значение (при необходимости).

Настраиваемые планки погрешностей нужно еще немного поработать.

С настраиваемыми планками ошибок может быть два сценария:

1. Все точки данных имеют одинаковую изменчивость
2. Каждая точка данных имеет свою изменчивость

Давайте посмотрим, как это сделать в Excel.

Настраиваемые полосы ошибок — одинаковая изменчивость для всех точек данных

Предположим, у вас есть набор данных, показанный ниже, и диаграмма, связанная с этими данными.

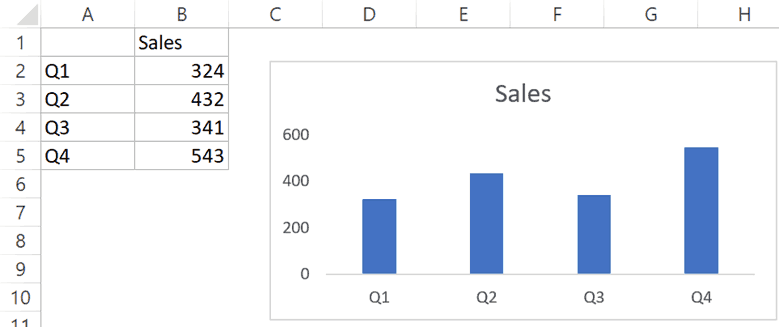
Ниже приведены шаги по созданию настраиваемых планок погрешностей (где значение ошибки одинаково для всех точек данных):

1. Щелкните в любом месте диаграммы. Это сделает доступными три значка параметров диаграммы.
2. Щелкните значок плюса (значок элемента диаграммы)
3. Щелкните значок черного треугольника справа от параметра «Полосы ошибок».
4. Выберите «Дополнительные параметры»
5. На панели «Форматировать шкалы ошибок» установите флажок «Пользовательский».

6. Нажмите кнопку «Указать значение».

7. В открывшемся диалоговом окне «Пользовательская ошибка» введите положительное и отрицательное значение ошибки. Вы можете удалить существующее значение в поле и ввести значение вручную (без знака равенства или скобок). В этом примере я использую 50 в качестве значения шкалы ошибок.
8. Нажмите ОК.

При этом будут применяться одни и те же настраиваемые планки погрешностей для каждого столбца гистограммы.

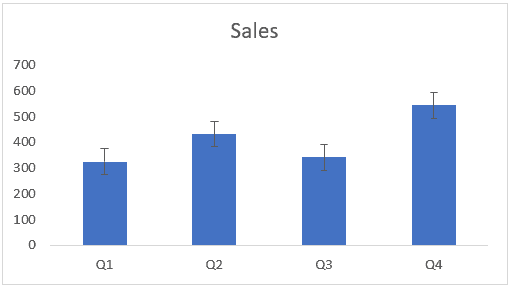
Настраиваемые полосы ошибок — различная изменчивость для всех точек данных

Если вы хотите иметь разные значения ошибок для каждой точки данных, вам необходимо иметь эти значения в диапазоне в Excel, а затем вы можете ссылаться на этот диапазон.

Например, предположим, что я вручную вычислил положительные и отрицательные значения ошибок для каждой точки данных (как показано ниже), и я хочу, чтобы они были нанесены на график в виде столбцов ошибок.

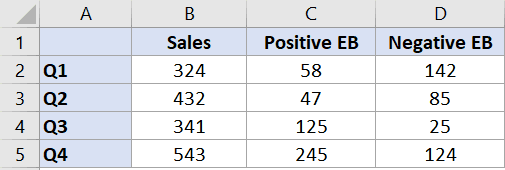
Ниже приведены шаги для этого:

1. Создайте столбчатую диаграмму, используя данные о продажах
2. Щелкните в любом месте диаграммы. Это сделает доступными три значка, как показано ниже.
3. Щелкните значок плюса (значок элемента диаграммы)
4. Щелкните значок черного треугольника справа от параметра «Полосы ошибок».
5. Выберите «Дополнительные параметры»
6. На панели «Форматировать шкалы ошибок» установите флажок «Пользовательский».

7. Нажмите кнопку «Указать значение».

8. В открывшемся диалоговом окне Custom Error щелкните значок переключателя диапазона для положительного значения ошибки, а затем выберите диапазон, который имеет эти значения (C2: C5 в этом примере).
9. Теперь щелкните значок переключателя диапазона для значения отрицательной ошибки, а затем выберите диапазон, который имеет эти значения (D2: D5 в этом примере).
10. Нажмите ОК.

Вышеупомянутые шаги предоставят вам настраиваемые планки ошибок для каждой точки данных на основе выбранных значений.

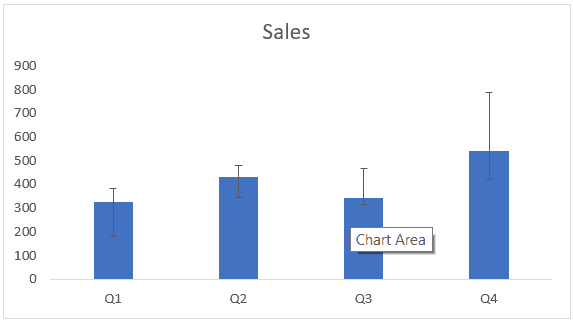
Обратите внимание, что каждый столбец в приведенной выше диаграмме имеет полосу ошибок разного размера, поскольку они были указаны с использованием значений в столбцах «Положительный EB» и «Отрицательный EB» в наборе данных. Если вы измените какое-либо из значений позже, диаграмма обновится автоматически

Если вы измените какое-либо из значений позже, диаграмма обновится автоматически.

Как добавить полосы ошибок в диаграммы Excel

В Excel вы можете добавлять полосы погрешностей на двухмерную линейную, столбчатую, столбчатую или диаграмму с областями. Вы также можете добавить его в точечную диаграмму XY или пузырьковую диаграмму.

Предположим, у вас есть набор данных и диаграмма (созданная с использованием этого набора данных), как показано ниже, и вы хотите добавить в этот набор данных планки погрешностей:

Ниже приведены шаги по добавлению гистограмм в Excel (2019/2016/2013):

1. Щелкните в любом месте диаграммы. Это сделает доступными три значка, как показано ниже.
2. Щелкните значок плюса (значок элемента диаграммы)
3. Щелкните значок черного треугольника справа от опции «Полосы ошибок» (она появляется, когда вы наводите курсор на опцию «Полосы ошибок»).
4. Выберите один из трех вариантов (Стандартная ошибка, Процент или Стандартное отклонение) или нажмите «Дополнительные параметры», чтобы получить еще больше вариантов. В этом примере я нажимаю на опцию «Процент».

Вышеупомянутые шаги добавят шкалу процентной ошибки ко всем четырем столбцам диаграммы.

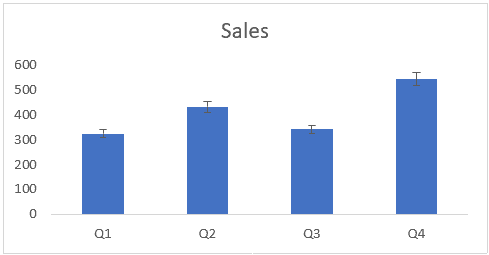
По умолчанию значение шкалы процентной ошибки составляет 5%. Это означает, что он создаст полосу ошибок, которая будет максимум на 5% выше и ниже текущего значения.

А что дальше?

Ещё одним важным моментом является то, что коэффициент корреляции позволяет оценить степень тесноты связи между результативным признаком (y) и воздействующим на него фактором (х), но не даёт ответа на вопрос: на сколько единиц изменится результативный признак при изменении фактора на одну единицу? .

Ответ на этот вопрос можно получить при помощи другого инструмента – регрессионного анализа. Объяснение сути данного анализа выходит за рамки настоящей темы, но с ней можно самостоятельно ознакомиться по различным источникам, например по источнику .

Вместе с тем один сугубо практический совет на этот счёт мы дадим.

В любой диаграмме рассеяния, построенной в последних версиях программы Excel, можно мгновенно, путём нажатия мышкой на соответствующее поле, как показано на рисунке ниже, построить «линию тренда», т.е. ту самую воображаемую среднюю линию, о который мы говорили выше. Она и даст нам общее представление о характере и величине изменения результативного признака y при изменении воздействующего на него фактора х:

Описание представленного инструмента контроля качества мы постарались изложить в максимально простой и доступной форме – в расчёте на то, что его будут читать и, надеемся, применять в работе в том числе и далёкие от математики люди.

Что показывает диаграмма рассеяния

Диаграмма рассеяния – один из инструментов статистического контроля, анализа. С ее помощью выявляется зависимость и характер связи между двумя разными параметрами экономического явления, производственного процесса. Диаграмма разброса показывает вид и тесноту взаимосвязи между парами данных. К примеру, между:

1. качеством продукта и влияющим фактором;
2. двумя разными характеристиками качества;
3. двумя обстоятельствами, влияющими на качество, и т.п.

Диаграммы рассеяния применяются для обнаружения корреляции между данными. Если корреляционная зависимость присутствует, то установить контроль над наблюдаемым явлением значительно проще.



Что учитывать при выборе бизнес идеи?

Выбирая бизнес идею, необходимо учитывать следующие факторы.

Современность товаров или услуг, способов их продажи

Некоторые идеи становятся устаревшими уже по истечению нескольких лет. Например, нанимать
коммивояжеров, чтобы они напрямую распространяли товары, еще пару лет назад было выгодной идеей,
особенно, если такой продукции не могли предложить конкуренты. Но сейчас с большой долей
вероятности такой бизнес потерпит катастрофу.

Наличие постоянной клиентской аудитории

Разумно выбрать такую идею, которая охватывала бы максимально широкий круг населения, или
наоборот, максимально специфический, требующий уникальных услуг. К примеру, открывать барбершоп стоит, если город довольно большой, и есть
достаточно людей, постоянно пользующихся услугами. Если нет уверенности, что клиентов будет
достаточно, лучше открыть обычную парикмахерскую.

Отсутствие прямых конкурентов

При наличии, например, супермаркета по соседству лучше не открывать маленький продуктовый
магазин – большинство решит пойти в привычное место.

Высокое качество предлагаемых товаров или услуг

Задача рекламы и маркетинга – привлечь покупателя. Удержать его сможет лишь качество
предлагаемой продукции или услуг.

Вставка точечной диаграммы в Excel

Предположим, у вас есть два столбца данных в Excel, и вы хотите вставить точечную диаграмму, чтобы проверить взаимосвязь между этими двумя переменными.

Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)

Начните с выбора данных в двух столбцах. Затем нажмите на Вставить вкладка на лента и найдите Графики раздел. Нажмите на кнопку с надписью рассеивать а затем выберите кнопку из меню под названием Разброс только с маркерами,

В более новых версиях Excel точечные диаграммы будут отображаться в виде маленькой кнопки с графиком и точками, как показано ниже. Кроме того, вы выберете просто рассеивать из выпадающего списка.

Теперь у вас должен быть точечный график с вашими данными, представленными на графике.

Добавить линию тренда в Excel

Теперь, когда у вас есть график рассеяния на листе Excel, вы можете добавить свою линию тренда. Начните, нажав один раз на любую точку данных на графике рассеяния. Это может быть сложно, потому что есть много элементов диаграммы, которые вы можете щелкнуть и отредактировать.

Вы будете знать, что выбрали точку данных, когда выбраны все точки данных. Выбрав точки данных, щелкните правой кнопкой мыши любую точку данных и выберите Добавить линию тренда из меню.

Теперь вы должны смотреть на Формат Trendline окно. Это окно содержит много опций для добавления линии тренда в график рассеяния Excel.

Обратите внимание, что вы можете добавить экспоненциальный, линейный, логарифмический, многочлен, Сила, или Скользящая средняя линия тренда / регрессии. Пока оставьте значение по умолчанию линейный опция выбрана

Нажмите на близко Кнопка и ваш график теперь должны отображать линию тренда линейной регрессии

Пока оставьте значение по умолчанию линейный опция выбрана. Нажмите на близко Кнопка и ваш график теперь должны отображать линию тренда линейной регрессии.

Как и во всех вещах Microsoft Office, вы можете отформатировать свою линию тренда так, чтобы она выглядела именно так, как вы хотите. В следующем разделе мы обсудим некоторые наиболее популярные изменения, которые вы можете внести в свою линию тренда, чтобы она выделялась.

Форматирование Excel Trendline

Чтобы отформатировать вновь созданную линию тренда, начните с щелчка правой кнопкой мыши по линии и выбора Формат Trendline из меню. Excel снова откроет Формат Trendline панель.

Один из наиболее популярных вариантов, которые люди используют при добавлении линии тренда в Excel, заключается в отображении как уравнения линии, так и значения R-квадрата прямо на графике. Вы можете найти и выбрать эти опции внизу окна. Пока выберите оба эти варианта.

Допустим, мы хотим, чтобы наша линия тренда отображалась более четко на графике. В конце концов, линия тренда по умолчанию имеет ширину всего в один пиксель и может иногда исчезать среди цветов и других элементов на графике. На левой стороне Формат Trendline нажмите на Fill & Line значок.

В этом окне измените ширина значение от 0,75 до примерно 3 и измените Тип тире к Квадратная точка вариант (третий в выпадающем меню). Просто чтобы продемонстрировать, что опция существует, измените Тип конца вариант со стрелкой.

Когда вы закончите, нажмите Икс кнопка на Формат Trendline панель и обратите внимание на изменения вашего точечного графика. Обратите внимание, что уравнение линии и значения R-квадрата теперь отображаются на графике и что линия тренда является более заметным элементом диаграммы

Как и многие функции в Excel, у вас есть практически безграничные опции, доступные вам при отображении линии тренда на диаграмме рассеяния.

Вы можете изменить цвет и толщину линии и даже добавить к ней 3D-элементы, такие как эффект затенения (нажмите на Последствия значок).

То, что вы выберете, зависит от того, насколько заметно вы хотите, чтобы ваша линия тренда выделялась на вашем графике. Поэкспериментируйте с опциями, и вы можете легко создать профессионально выглядящую линию тренда в Excel. Наслаждайтесь!

Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)

Что ещё важно знать

Следует учесть, что данный инструмент (диаграмма рассеяния и расчёт коэффициента корреляции) не является стопроцентной гарантией того, что две переменные, имеющие высокий коэффициент корреляции, действительно связаны между собой: существуют так называемые ложные корреляции, при которых расчётное значение коэффициента корреляции высоко, но при этом зависимости одного признака от другого нет. Причины возникновения ложных корреляций могут быть самыми разнообразными, например наличие какого-либо другого, скрытого от нас признака, который влияет одновременно на оба исследуемых нами признака. Так, цена продуктов питания и стоимость жилья могут показывать высокий коэффициент корреляции, но на самом деле эти величины связаны не между собой, а с инфляцией или с ростом стоимости производства. Подобные ситуации – ловушка для исследователей .

Возможны и обратные ситуации: связь реально существует, но установить её данным инструментом не удалось. Причины этого опять-таки могут быть самыми разными – от недостаточного числа собранных данных до чрезмерно большой ошибки измерения .

Но это не значит, что данным инструментом нельзя пользоваться! Наоборот, это достаточно простое, но эффективное средство статистического анализа. Необходимо всего лишь учитывать, что, во-первых, правильно диаграмму рассеяния и коэффициент корреляции могут оценить только те, кто хорошо знаком с исследуемым процессом; во-вторых, полученный таким образом коэффициент корреляции – это величина случайная и физической константой не является .

Иными словами, применение данного инструмента требует известной доли осторожности, внимания к деталям и знания сути вопроса

Диаграмма рассеяния в EXCEL

Диаграмма рассеяния ( scatter plot ) используется для отображения возможной взаимосвязи между двумя переменными. Диаграмма рассеяния незаменима при проведении корреляционного и регрессионного анализа.

Возьмем 2 переменные Х и Y и, соответственно, выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности зададим различные типы зависимости между переменными: линейную, квадратичную и затухающую синусоидальную. Для этого сгенерируем соответствующие тренды и настроим случайный разброс переменной Y (по нормальному закону ).

Сначала рассмотрим линейный тренд Y = aX + b (см. Файл примера, лист Линейный ). Параметры тренда (прямой линии) a и b зададим в отдельной табличке, там же зададим параметры отвечающие за величину дисперсии переменной Y.

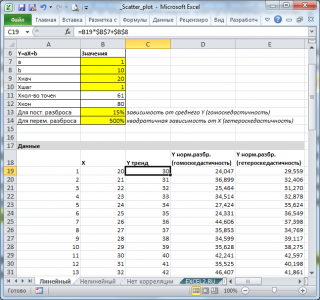
Величину постоянного разброса (отвечающую за гомоскедастичность модели) будем задавать в % от среднего значения Y. Иногда, дисперсия переменной Y не постоянна (имеется неоднородность наблюдений — гетероскедастичность ). Поэтому, при построении формул учтем и такую возможность.

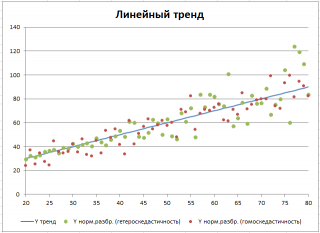
Для построения диаграммы рассеяния в файле примера использована диаграмма График , т.к. шаг по Х у нас задан постоянным. В случае реальных данных (переменная Х является случайной величиной, а не жестко заданной, как в нашем примере) используйте диаграмму типа Точечная. В файле примера реализовано оба варианта.

Примечание : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .

Отображение информации о 3-х переменных на двухмерной диаграмме

Предположим, что у нас имеются результаты измерения производительности некого непрерывного производственного процесса. Измерения проводились при различных рабочих температурах протекания процесса и в двух режимах.

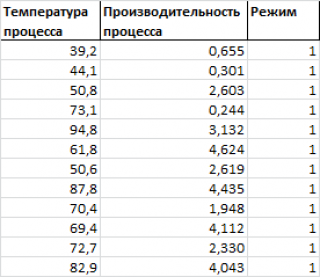
Нам требуется построить двумерную диаграмму рассеяния (на плоскости), хотя у нас имеется 3 переменных: производительность, температура и режим .

Обратим внимание, что третья переменная Режим является категориальной (принимает только значения из ограниченного набора значений). В нашем случае переменная Режим принимает 2 значения: Режим №1 и Режим №2 (значения 1 и 2 присвоены номинально)

Пары значений ( производительность; температура ), относящиеся к Режиму №1 будем на диаграмме рассеяния выводить красным цветом, а относящиеся к Режиму №2 будем выводить синим ( файл примера лист 3-переменных ).

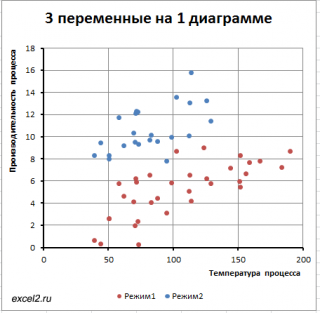
Такой же подход можно использовать для дискретных переменных , когда они принимают небольшое количество значений: 2-5.

Категоризованные диаграммы

Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые категоризованные диаграммы (coplot = conditioning plot).

Теперь вместо категориальной переменной Режим у нас имеется непрерывная переменная Давление , которая принимает значения от 10 до 20. Предположим, что значение переменной Давление = 15, является неким пороговым и протекание процесса значительно отличается, если оно протекает при давлении от 10 до 15 и от 15 до 20. Используя этот факт строят 2 диаграммы:

• Пары значений ( производительность; температура ) при давлении от 10 до 15:
• Пары значений ( производительность; температура ) при давлении от 15 до 20.

Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.

Матрица диаграмм рассеивания

Для множественной регрессии, когда имеется 3 или более переменных, часто строят Матрицу диаграмм рассеивания (Matrix Scatter Plot, Scatter Plot Matrix — SPM).

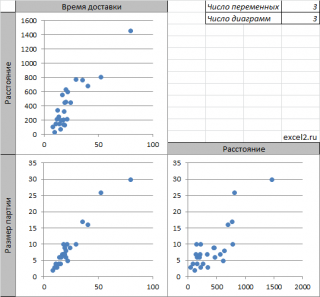
Если имеется 3 переменных (x 1 , x 2 , y), то строятся 3 обычные диаграммы рассеяния отображающие парные взаимосвязи переменных: (x 1 , x 2 ); (x 1 , y); (x 2 , y).

Примечание : Чтобы найти количество диаграмм рассеяния в матрице, необходимо вычислить число сочетаний из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ЧИСЛКОМБ(4;2) =6.

Иногда строят не только диаграмму (x 1 , x 2 ), но и (x 2 , x 1 ). В этом случае матрица будет содержать в 2 раза больше диаграмм рассеяния (см. файл примера лист Matrix ).

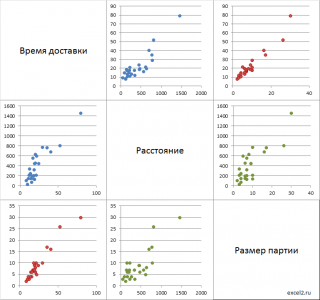
Примечание : Чтобы найти количество диаграмм рассеяния в такой (полной) матрице, необходимо вычислить число перестановок из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ПЕРЕСТ(4;2) =12.

Построение диаграммы рассеяния в Excel

Диаграмма разброса представляет наблюдаемое явление в пространстве двух измерений. Если одну величину рассматривать как «причину», влияющую на другую величину, то ей будет соответствовать ось Х (горизонтальная ось). Реагирующей на это влияние величине соответствует ось Y (вертикальная ось). Когда четко классифицировать переменные невозможно, распределение производится пользователем.

Построим диаграмму рассеяния для небольшой двумерной совокупности данных:

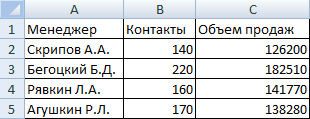
Предположим, что затраченные усилия каждого менеджера повлияли на результат его работы (так принято считать). Следовательно, число контактов необходимо показать на горизонтальной оси, а продажи (результат затраченных усилий) – на вертикальной.

Для построения диаграммы рассеяния в Excel выделим столбцы «Контакты», «Объем продаж» (включая заголовки). Перейдем на вкладку «Вставка» в группу «Диаграммы». Использование данного инструмента анализа возможно с помощью точечных диаграмм:

По умолчанию программа построила диаграмму разброса такого вида:

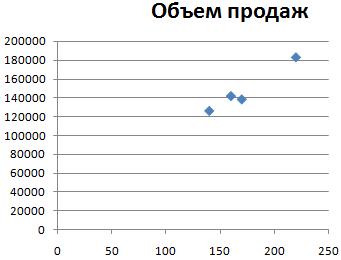
Изменим параметры горизонтальной и вертикальной оси, чтобы четыре пары показателей расположились более равномерно в области построения. Щелкнем сначала правой кнопкой мыши по вертикальной оси. Выберем «Формат оси»:

На вкладке «Параметры оси» установим минимальное значение 100 000, а максимальное – 200 000. Показатели объема продаж находятся в этих пределах:

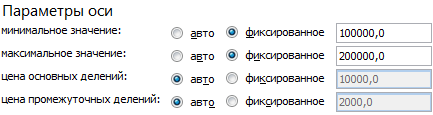
Минимальное значение для горизонтальной оси Х – 100, т.к. ниже этого показателя данных в таблице нет.

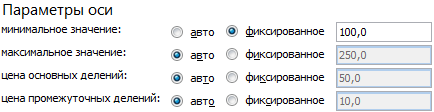
Диаграмма разброса приобрела следующий вид:

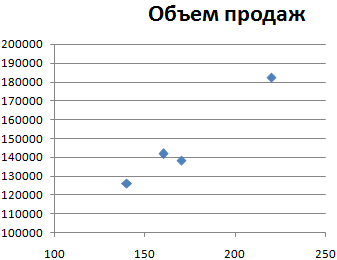
Какие можно сделать выводы по данной диаграмме рассеяния: