Диаграмма треугольник гранулометрического состава

Графическая обработка данных гранулометрического анализа

Лабораторная работа 4

Цель и содержание. Ознакомить студентов с графическими методами обработки данных гранулометрического анализа и использованием этих данных в генетических целях. В методических указаниях дается краткая характеристика наиболее распространенных способов графической обработки данных гранулометрического анализа, оценивается степень их наглядности и применимости и приводится методика построения различных графиков. Знания, полученные при выполнении этой работы, используются студентами при выполнении курсовой работы по дисциплине «Литология».

Теоретическое обоснование.

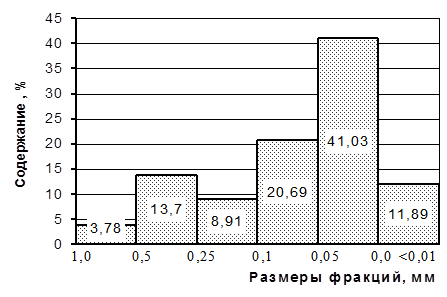
Самый наглядный график — гистограмма, на котором содержание каждой фракции изображается отдельно, чаще всего высотой столбика (рис.10).

Рисунок 10 — Гистограмма

Достоинство гистограмм — большая наглядность и возможность показа раздельно любой фракции. Недостаток — невозможность совмещения на одной диаграмме нескольких анализов. По гистограммам и кривым распределения, на которых отчетливо отображается как диапазон размерностей зерен, участвующих в строении породы, так и размер преобладающих фракций и ее содержание, может быть произведена оценка отсортированности породы.

По ее виду кривой распределения можно судить об отсортированности породы: высокая, узкая вершина будет у хорошо отсортированных пород; менее резкая — у плохо отсортированных.

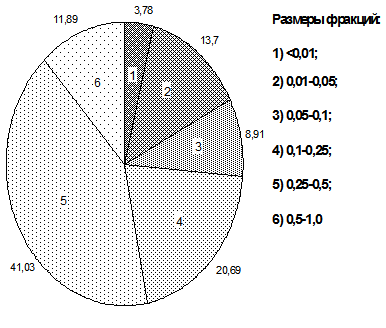Циклограмма

Рисунок 11 — Циклограмма

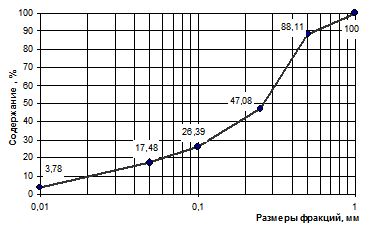Кумулятивные или суммарные

Рисунок 12 –Кумулятивная кривая

Простейшим математическим способом обработки кумулятивных кривых является вычисление трех гранулометрических коэффициентов: среднего размера зерен, коэффициента сортировки и коэффициента асимметрии. Средним или медианным диаметром (Мd) называется такой размер зерен, меньше и больше которого содержится по 50% частиц.

Величина коэффициента сортировки So характеризует степень однородности обломочного материала в породе. So всегда > 1 (обычно от 1,5 до 3), лишь для абсолютно однородного песка, состоящего из обломков, принадлежащих одной фракции, So = 1. Часто So (особенно в иностранной литературе) определяют по соотношению

Отсортированность песков определяется по таблице:

Степень отсортированности песков	So=Qз / Q_{1 —}	So= √Q₃/Q₁
Хорошо отсортированы	1 — 2,5	1 — 1,58
Средне отсортированы	2,5 — 4, 5	1,58- 2,12
Плохо отсортированы	> 4,5	> 2,5

Коэффициент асимметрии Sк указывает, в какую сторону (больших или меньших размеров) сдвинута мода (диаметр наиболее распространенных частиц) относительно вычисленного медианного диаметра. По кумулятивной кривой можно определить коэффициент К, характеризующий крупнозернистую часть породы. Эта величина характеризует такую размерность зерен, относительно которой более крупные зерна, встречаемые в породе, составляют 1% от всей породы. Крупнозернистая часть важна в том отношении, что она соответствует максимальной силе потока.

Треугольные диаграммы применяют для сопоставления результатов многих анализов — в этом его преимущество перед всеми ранее рассмотренными. Анализы здесь изображаются одной точкой, но содержания фракций определены быть не могут, т.к. при нанесении на треугольную диаграмму, допускающую показ лишь трех компонентов, фракции объединяются.

Материалы. Таблицы данных гранулометрического анализа, полулогарифмическая сетка для построения кривых распределения и кумулятивных кривых, сетка с двойным логарифмическим масштабом для построения генетической диаграммы Пассега.

Источник

Задача 1

По результатам
лабораторных исследований свойств грунтов:

а). построить для образцов песчаного
грунта интегрированную кривую гранулометрического состава, определить тип
грунта по гранулометрическому составу и степени его неоднородности, произвести
оценку плотности сложения и степени водонасыщения; для образцов глинистого
грунта определить тип грунта по числу пластичности и разновидность по
показателю текучести, произвести предварительную оценку способности грунта к
просадочному и набухающему явлениям по исходным данным из таблицы 1

Таблица 1 — Исходные
данные к задаче 1а

Плот-ность частиц
грунта

ρs,
(т/м3)

Плот-ность грунта

ρ, (т/м3)

Природ-ная

влаж-ность ω,

доли
ед.

Влажность

границы раскатывания ωр,
доли ед.

Влажность границы
текучести ωL, доли ед.

Содержание частиц, при
их размере

>2,0

2,0-0,5

0,5-0,25

0,25-0,1

0,1-0,05

0,05-0,01

0,01-0,005

< 0,005

2,73

(2,66)

1,94 (1,89)

0,19 (0,15)

0,23

0,42

3,8

29,8

29,4

18,5

11,5

4,6

1,1

1,3

Суммарный состав частиц
крупнее 2 мм. составляет 3,8% значит, песок не гравелистый; суммарный состав
частиц крупнее 0,5 мм. составляет 33,6% значит, песок не крупный; суммарный
состав частиц крупнее 0,25 мм. составляет 63% значит, грунт относится к песку
средней крупности.

Для определения
однородности грунта необходимо построить кривую однородности грунта, в которой
по оси абсцисс откладывают диаметры частиц в миллиметрах, а по оси ординат –
процентное содержание частиц нарастающим итогом.

По степени неоднородности
гранулометрического состава определяем по формуле

где —
диаметры частиц, определяемые по кривой однородности. Пересечения полученной
кривой с линиями, которые соответствуют содержанию частиц ,
дают искомые значения диаметров (рисунок 1).

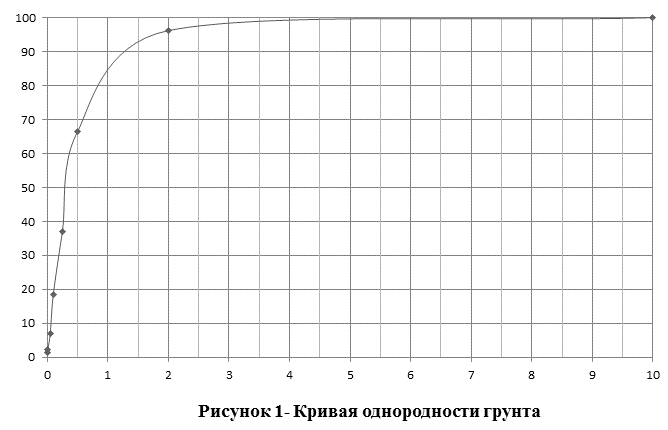
Так как то
по гранулометрической степени грунт является неоднородным.

Важным показателем оценки
свойств грунта является плотность их сложения. Плотности сложения песка зависят
от коэффициента пористости в естественном состоянии. Значение коэффициента
пористости можно определить по формуле:

где —
плотность частиц грунта (2,66 т/м3); —
природная влажность грунта (0,15); —
плотность грунта (1,89 т/м3).

По коэффициенту пористости можем сказать, что
наш грунт средней плотности.

Разновидность грунта по
степени влажности определяем по коэффициенту водонасыщения:

где
–
плотность воды (1 т/м3).

Коэффициент водонасыщения
равен 0,646, следовательно, грунт средней степени водонасыщения.

Вывод: исследуемый грунт
является песком средней крупности, неоднородным, средней плотности и средней
степени водонасыщения.

Определение глинистого
грунта.

Пластичность грунта
определяют в % по формуле:

где —
влажность на границе текучести грунтов (0,42=42%); —
влажность на стыке раскатывания грунта (0,23=23%).

Также благодаря этим
показателям можно определить характеристику текучести грунта

По полученным результатам
можем сделать вывод, что исследуемый грунт по пластичности – глина (легкая пылеватая
глина), по степени текучести – глина твердая.

В подгруппе пылевато —
глинистых грунтов выделяются грунты, обладающие просадочными свойствами. Под
действием внешних нагрузок или собственного веса при замачивание эти грунты
дают просадку. Поэтому необходимо определить степень просадки грунта.

Для предварительной
оценки к просадочным и набухающим свойствам необходимо определить :

где –
коэффициент пористости при влажности на границе текучести равный

По результату ,
следовательно, грунт просадочный; —
грунт не набухающий.

Вывод: по исследованиям
мы определили, что этот грунт легкая пылеватая глина, твердая, просадочная, но
не набухающая.

б).
построить график компрессионной зависимости вида ;
определить для заданного расчетного интервала давлений коэффициент
относительной сжимаемости грунта и охарактеризовать степень его сжимаемости.
Необходимые данные сведены в таблицу 2.

Таблица
2 – Исходные данные к задаче 1б

Начальный коэффициент пористости грунта	Полная осадка образца грунта S_i, при нагрузке P_i.	Расчетный интервал давлений
0,05	0,1	0,2	0,3	0,5	P₁	P₂
0,681	0,14	0,29	0,43	0,56	0,7	0,05	0,2
При определении коэффициента пористости начальная высота образца грунта равна 20 мм.

Для определения
коэффициента относительной сжимаемости грунта необходимо вычислить коэффициенты
пористости грунта, соответствующие заданным ступеням нагрузки по формуле:

где —
начальное значение коэффициента пористости грунта; —
полная осадка

Пример 3. Косвенный метод определения плотности p песков по результатам статического зондирования

Широко известно, что отобрать образцы песка действительно ненарушенной структуры из инженерно-геологических скважин даже на сегодняшний день чрезвычайно затруднительно, особенно на значительных глубинах и в случаях, когда такие грунты обводнены. Это подтверждал и Лев Геннадьевич Мариупольский в книге «Исследования грунтов для проектирования и строительства свайных фундаментов», Москва, Стройиздат 1989.

В качестве альтернативы лабораторному методу определения плотности природного сложения аллювиальных и флювиогляциальных песков, залегающих на глубине до 6 м, Л.Г. Мариупольским была предложена возможность определения p с помощью результатов статического зондирования, природной влажности (W) и плотности частиц грунта (p_s). Сопоставив 171 определение коэффициента пористости е, полученного в лабораторных условиях из ненарушенных образцов проб песка с сопротивлением конусу (q_c) зонда II типа этих же грунтов, выведена следующая корреляционная зависимость:

где 1 – это 1 МПа.

По утверждениям автора, коэффициент корреляции для такой зависимости составил 0,74, а среднее квадратическое отклонение – 0,09. Причем гранулометрический состав в таком случае практически не влияет на точность определения e.

Исходя из вышесказанного, получена формула количественного определения плотности p таких песков:

p_s— плотность частиц грунта;

W- влажность грунта;

e– коэффициент пористости.

Если подставить в эту формулу коэффициент пористости, то получится следующее:

Т.к. для определения W и p_s нет необходимости отбирать образцы ненарушенной структуры, то, по утверждениям автора, точности результатов p по данной формуле достаточно для расчетов оснований свайных фундаментов.

В следствии этого была представлена таблица, в которой приведены значения плотности p песков в зависимости от их q_c и W.

Таблица 1. Значения плотности песков p в зависимости от сопротивления конусу зонда q_c и влажности W по Мариупольскому

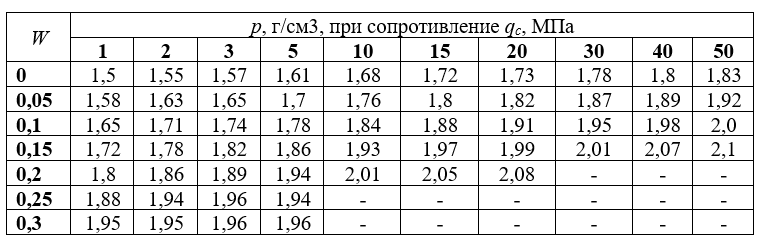
Для расчета значений в этой таблице, плотность частиц песков принималась, как средняя, p_s=2,65 г/см3.

Это было небольшое отступление. В данном примере не рассматривается вариант применения такого расчета для определения плотности песков. Цель – показать возможность интерполяции по двум неизвестным, для которого хорошо подходит такая таблица.

Теперь перенесем ее на новый лист Excel. Чтобы еще немного усложнить задачу, расположим значения в строке q_c от большего к меньшему. Соответственно, значения p тоже перенесем (рис. 14).

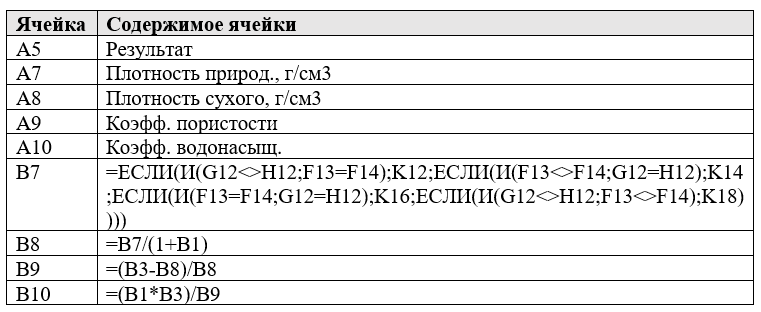
Рис. 14. Таблица 1 на листе Excel

Далее ход действий такой же, как и в предыдущих примерах. Формат ячеек может быть, как общий, так и числовой.

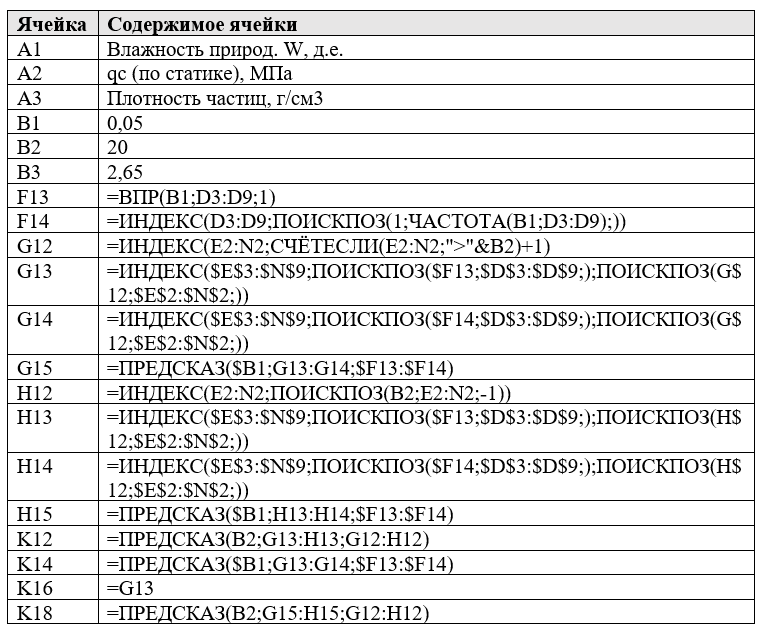
Теперь обработаем результаты, а заодно рассчитаем такие показатели, как плотность сухого грунта p_d, коэффициент пористости e и коэффициент водонасыщения S_r.

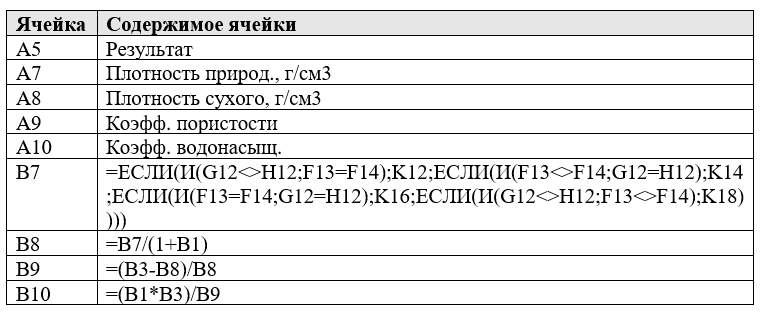
Дополнительно, помимо простой интерполяции, выполним расчет p по тем формулам, которые указывались выше:

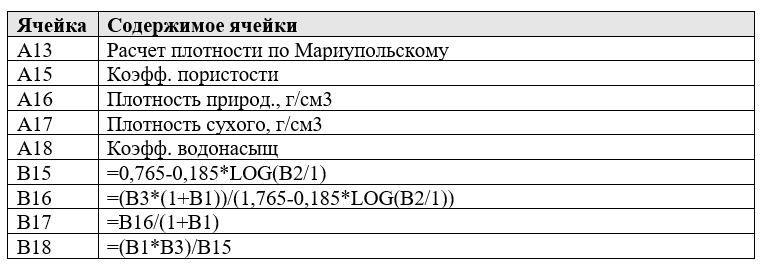
Теперь, лист Excel у вас должен иметь следующий вид (рис. 15)

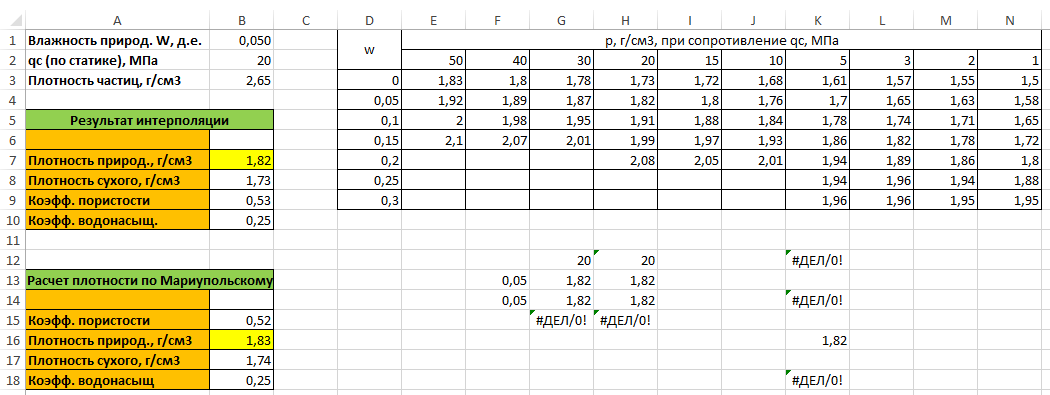
Рис. 15. Окончательный вид примера 3 на листе Excel

Изменяя значения в ячейках B1, B2 и B3, вы будете получать значения как по результатам интерполяции таблицы, так и по результатам расчета. Как вы можете заметить, они немного отличаются. Расчетные более точные, в том числе и потому, что указывается реальная плотность частиц, полученная в результате лабораторных исследований.

Примечание. Вы могли заметить, что таблица заполнена не полностью. И даже если указать в ячейке B1, например 0,25, а в ячейке B2– 40, интерполяция все равно будет выполнена. Только это, конечно уже будет экстраполяция. Чтобы этого избежать, можно не использовать условные операторы, как в предыдущих примерах, а заполнить пустые ячейки, например, словом «Ошибка» (рис. 16).

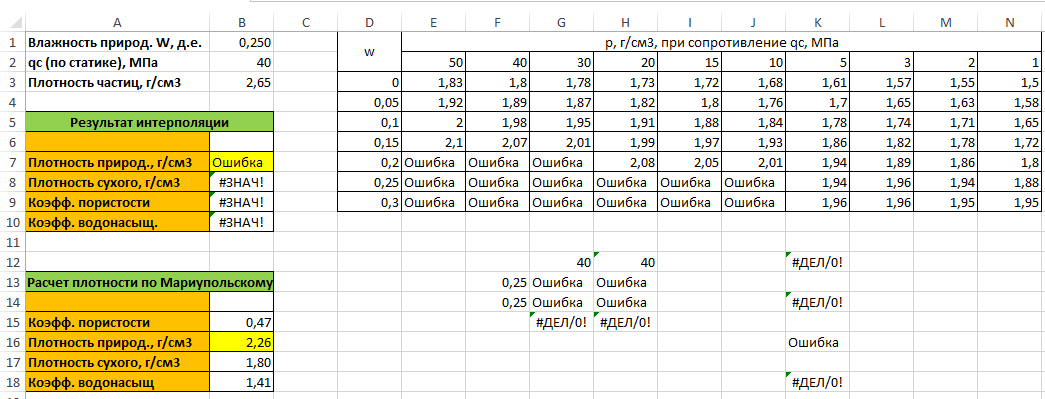
Рис. 16. Вариант запрета экстраполяции без использования условных операторов

В результате, в ячейке B7, вы получите «Ошибка» или #Н/Д.

ОБЪЕКТЫ И МЕТОДЫ

Изучали два слитоземных комплексов с микрорельефом гильгай в умеренной и субтропической
зонах. На разных элементах микрорельефа увлажненность сильно различается: в почвы
микропонижений поступает вдвое больше осадков, чем в почвы микроповышений.

Первый слитоземный комплекс расположен в Центральном Предкавказье на Ставропольской
возвышенности (44°38′12″ с. ш., 42°14′45″ в. д.) на глинистом элювии-делювии майкопских
глин в условиях умеренно-континентального климата. В микроповышении образовалась солонцеватая
темная почва, на микросклоне – типичная темная слитая, на микропонижении – гидрометаморфизированная
темная слитая почва, согласно [].

Второй слитоземный комплекс расположен на юге США, штат Техас, на второй надпойменной
террасе р. Бразос (30°29′21″ с. ш., 96°28′44″ з. д.) в условиях субтропического климата.
Почвообразующие породы – глинистый аллювий пермских и триасовых красноцветных глинистых
отложений. Почва на микроповышении и микросклоне классифицируется как типичная темная
слитая, а почва на микропонижении – как гидрометаморфизированная темная слитая [].

Гранулометрический состав почв определялся на лазерном дифракционном анализаторе размера
частиц “Analysette 22 comfort” (FRITSCH, Germany) []. В приборе используется метод “обратной оптики Фурье” ‒ система сходящегося лазерного
луча (гелий‒неоновый лазер с длиной волны 632.8 нм).

Перед анализом почвенные образцы в виде суспензии были обработаны ультразвуком без
предварительной химической обработки. Исходные образцы почв растирали пестиком с резиновым
наконечником и просеивали через сито 0.25 мм. К навеске (0.10–0.13 г) добавляли 30
мл дистиллированной воды и диспергировали почву ультразвуковым диспергатором Digital
Sonifir 250 (Branson Ultrasonics) с диспергирующим элементом зондового типа, работающем
на частоте 20 кГц, в неимпульсном режиме. Энергия ультразвука – 450 Дж/мл, что достаточно
для диспергации образцов большинства почв [].

Как построить интегральную кривую в excel

Требуется построить диаграмму стандартного нормального интегрального распределения (стандартное нормальное распределение имеет М = 0 и = 1), используя функцию НОРМСТРАСП.

1. В ячейку A3 введем символ х, а в ячейку ВЗ — символ функции плотности вероятности f(x).

2. Вычислим нижнюю М — За границу диапазона значений х, для чего установим курсор в ячейку С2 и введем формулу =0-3*1, а также верхнюю границу — в ячейку Е2 введем формулу =0+3*1.

3. Скопируем формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифметической прогрессии.

4. Создадим последовательность значений х в требуемом диапазоне, для чего установим курсор в ячейку А4 и выполним команду меню Правка/Заполнить/Прогрессия.

5. В открывшемся окне диалога Прогрессия установим переключатели арифметическая, по столбцам, в поле Шаг введем значение 0,5, а в поле Предельное значение — число, равное верхней границе диапазона.

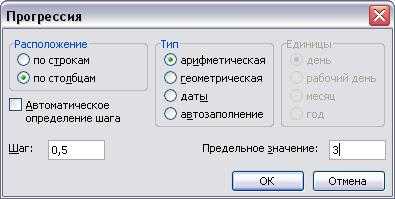
Функция НОРМРАСПР в EXCEL

6. Щелкнем на кнопке ОК. В диапазоне А4:А16 будет сформирована последовательность значений х.

7. Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций — НОРМРАСП.

8. Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее — введем число 0, для параметра Стандартное_откл — число 1, для параметра Интегральное — число 0 (весовая).

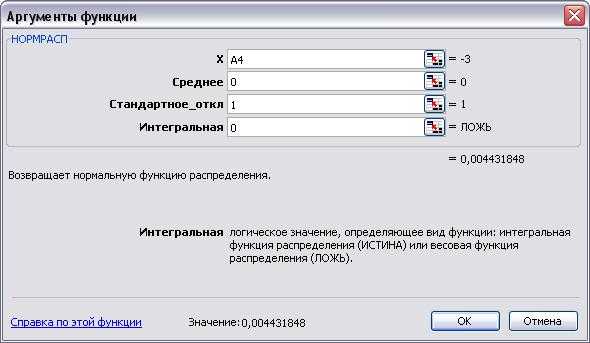
Диаграмма нормального интегрального распределения в EXCEL

9. Используя маркер буксировки, скопируем полученную формулу в диапазон ячеек В5:В16.

10. Выделим диапазон полученных табличных значений функции f(х) (ВЗ:В16) и выполним команду меню Вставка/Диаграмма. В окне Мастер диаграмм во вкладке Стандартные выберем График, а в поле Вид — вид графика, щелкнем на кнопке Далее.

11. В окне Мастер диаграмм (шаг 2) выберем закладку Ряд. В поле Подписи оси х укажем ссылку на диапазон, содержащий значения х (А4:А16). Щелкнем на кнопке Далее. В окне Мастер диаграмм (шаг 3) введем подписи: Название диаграммы, Ось х, Ось у. Щелкнем на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности .

Характеристики нормального распределения

Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.

Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.

Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма

Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.

Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.

Как сделать линейную калибровочную кривую в Excel — gadgetshelp,com
Что касается настроек названия, подписей, осей и прочих в Office , то там это сделать еще проще и удобнее: достаточно пары кликов по изменяемым визуальным компонентам и использования привязанного к ним контекстного меню.

Как самостоятельно исследовать гранулометрический состав почвы?

Если в вашей местности нет квалифицированных геологов или их услуги слишком дорогие для ваших финансовых возможностей, можно воспользоваться несколькими известными методиками для ориентировочной оценки грунта.

Основные способы исследования почвы:

ситовой;
с помощью ареометра;
пипеточный;
метод двойного отмучивания по Сабанину — анализируется свободное падение частиц грунта в воде;
метод Рутковского (набухание глиняных частиц в воде, осаждение на дно емкости)

Мы приведем самый простой и распространенный, в том числе и среди дачников. Описываемый ниже нами способ похож на упрощенный метод определения состава грунтов Рутковского.

Отличить песок от глины сможет любой дачник или начинающий строитель — в некоторых случаях достаточно пройтись по такому грунту. Как правило, глина налипает на подошву обуви, а песок осыпается. Для того, чтобы приступить к обработке или застройке земли, этих наблюдений, конечно, недостаточно. Так возникает необходимость в исследовании механического состава земли.

Приведенный нами способ определения гранулометрического состава заключается в анализе времени, которое занимает процесс оседания различных по весу частиц грунта на дно емкости, заполненной водой, а также определении процентного соотношения глины / ила/ песка.

Возьмите со своего участка образец грунта, в котором вы хотите определить процентное соотношение глиняных, песчаных и пылеватых частиц, а лучше несколько проб грунта с разных частей участка (по пятну застройки, то есть где вы планируете строить дом). Глубина бурения грунта для взятия проб – от 4 метров (чем тяжелее дом, тем глубже стоит посмотреть).
Поместите образец грунта в стеклянную колбу или литровую банку. Грунта должно быть чуть меньше, чем половина.
В емкость налейте пару капель средства для мытья посуды, затем долейте до самого верха воды, оставляем где-то 2,5 см от края для воздуха, чтобы можно было смешать образец грунта с водой.
Закройте банку крышкой и с усилием трясем смесь 3-5 минут.
Вычислить количество частиц песка можно уже ч/з пару минут — он быстро оседает на дно емкости. Можете сразу отметить уровень оседания маркером.
Вычислить количество пылеватых частиц ила можно не ранее интервала в 2-3 часа. Вы заметите, как он уляжется на ранее осевший слой песка — нанесите маркером на емкость вторую метку.
Определить долю глины удастся лишь как минимум через сутки, как максимум — по истечению 2-5 дней, (банку не трогайте). Когда вода станет менее мутной, а грунт «усядется», нанесите последнюю метку на банку.

Далее гранулометрический состав почвы определяется исходя от вашего образца:

• высота от дна банки до третьей метки принимается за 100%;

• определяем долю каждого слоя из осадков и переносим итоговые числа в форму, используя метод треугольных координат – пользуемся треугольником Ферре;

Построение гистограммы с помощью надстройки Пакет анализа

Вызвав диалоговое окно надстройки Пакет анализа , выберите пункт Гистограмма и нажмите ОК.

В появившемся окне необходимо как минимум указать: входной интервал и левую верхнюю ячейку выходного интервала . После нажатия кнопки ОК будут:

автоматически рассчитаны интервалы значений (карманы);
подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.

Перед тем как анализировать полученный результат – отсортируйте исходный массив данных .

Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).

Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так: =(МАКС( Исходные_данные )-МИН( Исходные_данные ))/7 где Исходные_данные – именованный диапазон , содержащий наши данные.

Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).

Примечание Похоже, что инструмент Гистограмма для подсчета общего количества интервалов (с учетом первого) использует формулу =ЦЕЛОЕ(КОРЕНЬ(СЧЕТ( Исходные_данные )))+1

Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция ЦЕЛОЕ() округляет до ближайшего меньшего целого (ЦЕЛОЕ(КОРЕНЬ(35))=5 , а ЦЕЛОЕ(КОРЕНЬ(36))=6) .

Если установить галочку напротив поля Парето (отсортированная гистограмма) , то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.

Если установить галочку напротив поля Интегральный процент , то к таблице с частотами будет добавлен столбец с нарастающим итогом в % от общего количества значений в массиве.

Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка ).

Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.

В результате получим практически такую же по форме гистограмму , что и раньше, но с более красивыми границами интервалов.

наблюдать за динамикой

Как построить диаграмму

Аналогично графикам, диаграммы строятся на основе данных в столбцах таблицы, но для некоторых видов (круговые, кольцевые, пузырьковые и др.) нужно, чтобы данные располагались определенным образом. Чтобы построить диаграмму нужно перейти во вкладку Диаграммы. Для примера рассмотрим, как сделать круговую.

Диаграммы кругового типа демонстрируют пропорции частей относительно чего-то целого и представляются в виде совокупности секторов, входящих в состав круга с отображением соответствующих значений. Это очень полезно, когда требуется сравнить некоторые данные по отношению к суммарному значению.

Как построить гистограмму по данным таблицы в Excel

Идем во вкладку «Анализ данных» и выбираем «Гистограмма».
Выбираем входной интервал.
Здесь же предлагается задать интервал карманов, т.е. те диапазоны, в пределах которых будут лежать наши значения. Чем больше значений в интервале — тем выше столбик гистограммы. Если мы оставим поле «Интервалы карманов» пустым, то программа вычислит границы интервалов за нас.
Если хотим сразу же вывести график,то ставим галочку напротив «Вывод графика».
Нажимаем «ОК».
Вот, вроде бы, и все: гистограмма готова. Теперь нужно сделать так, чтобы по вертикальной оси отображалась не абсолютная частота, а относительная.
Под появившейся таблицей со столбцами «Карман» и «Частота» под столбцом «Частота» введем формулу «=СУММ» и сложим все абсолютные частоты.
К появившейся таблице со столбцами «Карман» и «Частота» добавим еще один столбец и назовем его «Относительная частота».
Во всех ячейках нового столбца введем формулу, которая будет рассчитывать относительную частоту: 100 умножить на абсолютную частоту (ячейка из столбца «частота») и разделить на сумму, которую мы вычислил в п. 7.

Гистограмма распределения – это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции ЧАСТОТА() и диаграммы.

Метод 1: используем инструменты на ленте программы

Это, пожалуй, самый простой способ. И вот, как он реализуется:

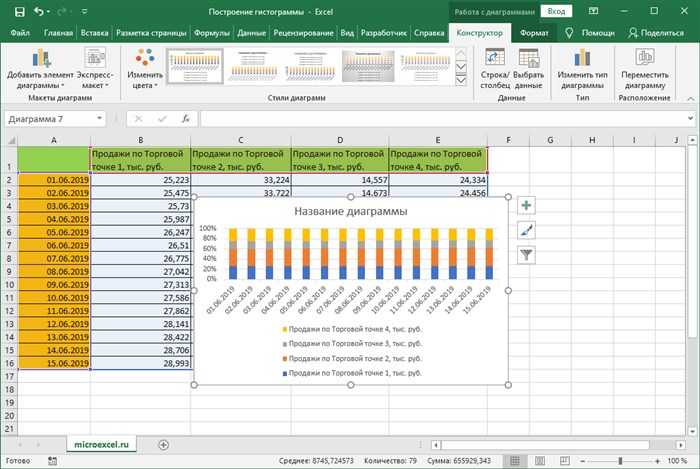
Открываем (или создаем) таблицу. Выделяем любым удобным способом (например, с помощью зажатой левой кнопки мыши) ячейки, на базе которых планируется построить диаграмму.

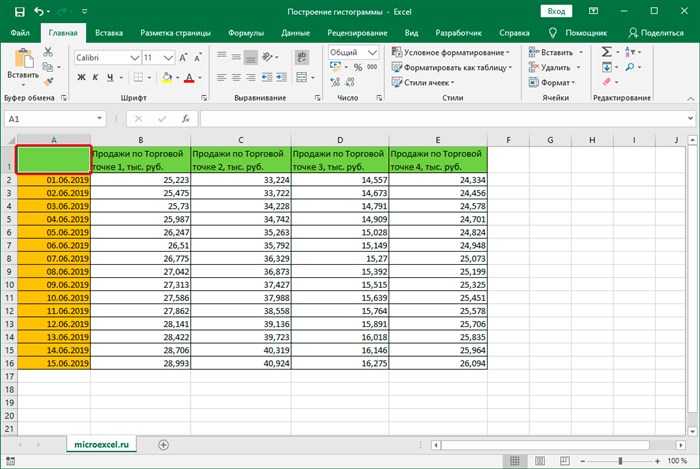
Гистограмма с накоплением До того, как приступить к созданию гистограммы с накоплением, проверяем, чтобы самая верхняя левая ячейка таблицы была пустой.Затем делаем следующее:

Примечание: в гистограммах с накоплением один столбец содержит сразу несколько значений. В нашем случае – это данные по всем четырем торговым точкам за конкретную дату.

Нормированная гистограмма с накоплением В данном случае отображается (в процентном выражении) вклад каждого значения в общем количестве.

Как сделать график распределения в excel?
Таким образом, линия, по сути, заполняет информацию между двумя известными для вас точками, так что вы можете быть достаточно уверенными при оценке фактической температуры, когда термометр показывает 57,2 градуса, но когда вы никогда не измеряли «стандарт», который соответствует это чтение.

Текст научной работы на тему «К вопросу о построении треугольных диаграмм в программе Microsoft Exel при изучении пород-коллекторов Штокмановского месторождения»

К ВОПРОСУ О ПОСТРОЕНИИ ТРЕУГОЛЬНЫХ ДИАГРАММ В ПРОГРАММЕ MICROSOFT EXEL ПРИ ИЗУЧЕНИИ ПОРОД-КОЛЛЕКТОРОВ ШТОКМАНОВСКОГО МЕСТОРОЖДЕНИЯ

И.Б. Крюкова (ООО «Газпром ВНИИГАЗ»)

Одной из удобных и наглядных форм представления результатов экспериментов является треугольная диаграмма, позволяющая показать несколько анализов на одном чертеже. Этот метод популярен в гранулометрии, геохимии, при анализе трехфазных сред и т.д. Однако, когда мы имеем дело с большим количеством данных, например, по результатам гранулометрического анализа пород, возникает проблема их автоматической обработки. Для этого удобно было бы воспользоваться программой Microsoft Exel, но в стандартном наборе возможных графиков отсутствуют треугольные диаграммы.

Эту проблему можно обойти, если при построении перейти от треугольных координат к стандартным прямоугольным путем замены переменных, и затем воспользоваться мастером диаграмм Microsoft Exel, выбрав тип диаграммы «точечная». Таким образом, программа будет наносить точки на стандартное поле в привычных координатах (x, y), но эти точки не будут выходить за рамки равностороннего треугольника, и их координаты будут в точности соответствовать исходным значениям на треугольных осях.

В исходных данных для треугольных диаграмм координаты каждой точки заданы в виде трех чисел (a; b; c), сумма которых равна 100:

Нужно отметить, что третья координата является номинальной и на самом деле на положение точки не влияет, так как рассчитывается из первых двух: еі = 100 — аі- Ь¡. Поэтому для замены переменных необходимо установить соответствие треугольных координат (а;; Ь) стандартным прямоугольным (х; уі).

Рассмотрим рис. 1. Мы видим треугольную диаграмму СВА и нанесенную на нее точку с координатами (а; Ь). На эту треугольную диаграмму наложены стандартные прямоугольные осиX, У, в проекции на которые координаты данной точки принимают значения (х; у) соответственно. Необходимо найти два уравнения замены переменных: х = /1(а, Ь) и у = /2(а, Ь).

ai + bi + c i = 100, i = 1. n, где n — количество точек.

Рис. 1. Схема перевода треугольных координат в прямоугольные

Из данного построения видно, что ось ординат Y полностью совпадает по направлению с осью, с которой снимается треугольная координата b, и эти координаты у данной точки полностью совпадают, т.е. первое уравнение замены переменной выглядит очень просто:

Для нахождения координаты x рассмотрим заштрихованные треугольники. Они подобны, и нам известны в них все углы (90°, 30° и 60°). В результате несложных геометрических вычислений полу-20 + b тт

чим выражение x = —р—. Но это еще не окончательный результат, так как максимальные значения V3

координат по прямоугольным и треугольным осям должны быть одинаковы (и равны 100), а в нашем построении длины отрезков осей X и Y от 0 до 100 соотносятся как высота и длина стороны равнобедренного треугольника, т.е. ^2-. Таким образом, учитывая поправочный коэффициент, получаем

Имея уравнения (1) и (2), мы можем без труда пересчитать в программе Microsoft Exel треугольные координаты на прямоугольные для любого, даже очень большого, количества точек и затем в прямоугольных координатах построить точечную диаграмму, которая будет выглядеть как треугольная.

На рис. 2 показан пример построения гранулометрического треугольника по результатам гранулометрического анализа керна, поднятого из скв. 7 Штокмановского месторождения, из интервала 1952-1997 м, пласт Ю0.

Рис. 2. Пример построения треугольной диаграммы

Исходные данные находятся в столбцах А, В, С и D. В ячейку Е2 нужно ввести формулу пересчета первой координаты (х): D2 + С2/2 и распространить ее на весь столбец. В ячейки F2-F16 (координата у) копируется столбец С. Далее с помощью мастера диаграмм выбираем «точечную диаграмму» и строим график на выборке (х, у).

Чтобы диаграмма выглядела как треугольная, ее необходимо подредактировать: в «параметрах диаграммы» сделать невидимой ось У и вручную с помощью панели инструментов «Рисование» нарисовать равнобедренный треугольник с основанием на оси абсцисс.

Данный метод может применяться не только для построения гранулометрического треугольника, но и для аналогичного вида треугольных диаграмм, например, при анализе минерального состава пород и других.

Пакет «анализ данных»

Атрибутивными — называют ряды распределения, построенные по качественными признакам.
Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными.

Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.

Домохозяйства, состоящие из:	одного человека	двух человек	трех человек	5 или более	всего
Число домохозяйств в %	19,2	26,2	22,6	20,5	100,0

Полезные сведения → Как объединить ячейки → Как вставить значения → Аргументы функции → Работа с форматами → Функция ЕСЛИ → Как удалить пробелы → Функция впр vlookup→ Работа с таблицами

ЗАКЛЮЧЕНИЕ

Процедура деконволюции для расщепления исходного спектра гранулометрического состава
на составляющие фракции помимо уточнения традициионных показателей дает новую информацию
о свойствах отдельных гранулометрических фракций. Разработанная методика дековолюции
исходных спектров гранулометрического состава апробирована на конкретных объектах:
слитых почвах двух разных регионов Мира. Благодаря деконволюции удалось выявить фракции,
“невидимые” при визуальном анализе исходного спектра частиц. К новым показателям относятся:
средний диаметр гранулометрической фракции d_ср и величина дисперсии D каждой фракции.

Распределение элементарных фракций слитых почв вполне согласуется с границами фракций
классификации FAO гранулометрического состава и не согласуется с границами классов
в классификации Качинского, так как в ней ширина классов варьирует: индекс F = 2 и 5. Преимущество классификации гранулометрического состава FAO в одинаковой
ширине фракций с постоянным значением F = 3.2.

Благодарность. Авторы благодарят Ю.А. Жукову и А.В. Юдину за помощь в проведении исследований. Отдельная
благодарность С.А. Шобе – за просмотр рукописи и полезные советы.