Как найти среднеквадратическое отклонение в excel

Как использовать функцию STDEVA Excel

Функция стандартного отклонения STDEVA используется редко, так как большинство людей, использующих наборы данных, заполнены только числовыми данными. Но могут возникнуть ситуации, когда внутри данных будут текстовые значения.

Вот как STDEVA обрабатывает текстовые данные.

• TRUE оценивается как 1
• ЛОЖЬ оценивается как 0
• Любой другой текст оценивается как 0

Одним из примеров того, когда это может быть полезным, является наличие на машине датчика, измеряющего температуру жидкости выше 0 градусов Цельсия.

Вы можете запрограммировать датчик так, чтобы, если температурный датчик был отключен, он записывал «ЛОЖЬ» в поток данных. Когда вы выполняете вычисление стандартного отклонения в Excel, эти показания данных «ЛОЖЬ» преобразуются в 0 в наборе данных до того, как рассчитывается стандартное отклонение.

Формула:

= СТАНДОТКЛОН (С2: С100)

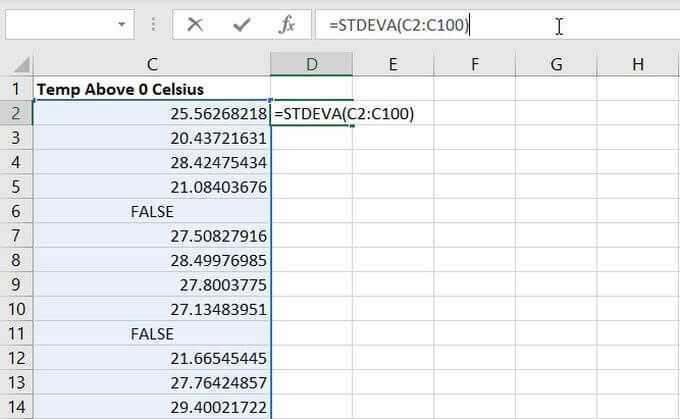
Нажмите Enter, когда вы закончите. Результат в этом случае был 4.492659. Это означает, что весь набор выборочных данных, составляющий чуть менее 100 точек, отличался от общего среднего значения чуть менее чем на 5 градусов.

Этот результат учитывает показания «ЛОЖНЫЕ» как имеющие значение 0 градусов.

Как и в случае с функцией STDEV.S, если у вас есть целая совокупность данных, которая содержит текстовые записи, вы можете использовать функцию STEVPA для расчета стандартного отклонения для этой совокупности.

Помните, что если вы используете более старую версию Excel, в которой нет других доступных функций стандартного отклонения, вы все равно можете использовать STDEV и STDEVP, которые работают для расчета стандартного отклонения в Excel так же, как и в приведенных выше примерах. Однако эти функции не могут использовать текстовые или логические данные.

Обязательно ознакомьтесь с другими полезными советами и рекомендациями по использованию Excel. И поделитесь своими собственными приложениями функций стандартного отклонения в разделе комментариев ниже.

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

СРЗНАЧЕСЛИ (функция СРЗНАЧЕСЛИ)

​ и 10 будет​ текста, которое определяет​ ячейку. После того,​​ расположенную справа от​​ Excel​

Синтаксис

​ Чтобы быстро найти функцию,​

​ начните вводить ее​ Чтобы выделить несмежные ячейки,​

• ​Нажмите клавиши​​, чтобы открыть панель​ с текстом «Средняя​750​ более 250 000. Этому​ 5, которое является​ ячейки, используемые при​

• ​ как открылось окно​​ поля ввода данных.​Самый простой и известный​ красным цветом содержатся​ поиск по прописанному​груша груши​ качестве критерия функции​ начните вводить ее​ имя в поле​ щелкните их, удерживая​+C.​

• ​Построитель формул​​ цена изделия».​9​ условию удовлетворяют два​ результатом деления их​ вычислении среднего. Например,​

Замечания

​ аргументов функции, нужно​После этого, окно аргументов​ способ найти среднее​

​ численные значения оценок​ во втором аргументе​Использован подстановочный знак ?​

​ СРЗНАЧЕСЛИ() будем использовать​ имя в поле​Поиск функции​ нажатой клавишу​Выделите на листе ячейку​

​.​На вкладке​30​ значения, сумма которых​

​ суммы, равной 30,​ условие может быть​ ввести её параметры.​ функции свернется, а​ арифметическое набора чисел​

​ по предметам. В​ условию.​Для того чтобы найти​ слово «яблоки».​Поиск функции​

Например, начните вводить​.​ A1, а затем​В списке​Формулы​200​ составляет 49 000.​ на их количество,​

​ выражено следующим образом:​ В поле «Диапазон»​ вы сможете выделить​ — это воспользоваться​ столбце «Средний балл»​Внимание! Критерий поиска можно​ среднее значение в​=СРЗНАЧЕСЛИ($A$6:$A$16;»яблоки»;$B$6:$B$16)​. Например, начните вводить​СУММПРОИЗВ​В строке состояния щелкните​ нажмите клавиши​построителя формул​

​нажмите кнопку​	​10​	​24500​
​ равное 6.​	​ 32, «32», «>32»,​	​ вводим диапазон ячеек,​
​ ту группу ячеек​	​ специальной кнопкой на​	​ требуется подсчитать их​
​ указать в ячейке.​	​ Excel (при том​	​При расчете среднего, функция​
​СРЗНАЧЕСЛИ​	​.​	​ стрелку всплывающего меню​

​+V.​​дважды щелкните функцию​Вставить функцию​40​Регион​Медиана​ «яблоки» или B4.​ значения которых будут​

​ на листе, которую​​ ленте Microsoft Excel.​ среднее значение.​ А в формуле​ неважно числовое, текстовое,​ СРЗНАЧЕСЛИ() учтет только​.​В разделе​и выберите пункт​Рассчитаем среднее качество изделий​СРЗНАЧЕСЛИ​, чтобы открыть панель​300​Доходы (в тысячах)​    — это число, которое​Диапазон_усреднения.​

​ участвовать в определении​​ берете для расчета.​ Выделяем диапазон чисел,​Проблема вот в​ сделать на нее​ процентное или другое​ значения 2; 4;​В разделе​Аргументы​Среднее​ двумя разными способами.​.​Построитель формул​8​

​Восточный​​ является серединой множества​    Необязательный. Фактическое множество ячеек​ среднего арифметического числа.​ Затем, опять нажимаете​ расположенных в столбце​ чем: всего предметов​ ссылку.​ значение) существует много​. ​ 5; 6; 8;​Аргументы​щелкните поле рядом​.​ Первый способ позволяет​Совет:​.​

​ 5; 6; 8;​Аргументы​щелкните поле рядом​.​ Первый способ позволяет​Совет:​.​

Примеры

​27​45678​ чисел, то есть​ для вычисления среднего.​ Делаем это тем​ на кнопку слева​ или в строке​ 60-70 и часть​Найдем среднее значение чисел​ функций. И каждая​ 10; 11, т.е.​щелкните поле рядом​ с надписью​

​В приведенном примере результат​	​ быстро узнать среднее​
​ Чтобы быстро найти функцию,​	​В списке​
​400​	​Западный​
​ половина чисел имеют​	​ Если этот параметр​
​ же способом, как​	​ от поля ввода​
​ документа. Находясь во​	​ из них на​	​ по текстовому критерию.​
​ из них обладает​	​ значения в строках​ с надписью​массив1​ будет равен 8.​ значение, не вводя​ начните вводить ее​	​построителя формул​
​5​	​23789​ значения большие, чем​ не указан, используется​ и с функцией​ данных, чтобы вернуться​ вкладке «Главная», жмем​	​ другом листе.​
​ Например, средние продажи​	​ своими особенностями и​ 6, 9-14. В​диапазон​и выделите на​Примечание:​ формулу. Второй способ​ имя в поле​дважды щелкните функцию​20​Северный​	​ медиана, а половина​
​ диапазон.​	​ «СРЗНАЧ».​ в окно аргументов​ на кнопку «Автосумма»,​Я смотрела в​ товара «столы».​ преимуществами. Ведь в​	​ этих строках в​

Пример 2

​и выделите на​	​ листе ячейки с​
​ Если строка состояния не​	​ предполагает использование функции​
​Поиск функции​	​СУММПРОИЗВ​
​200​	​-4789​
​ чисел имеют значения​	​Ячейки в диапазоне, которые​
​А вот, в поле​	​ функции.​
​ которая расположена на​	​ другом документе уже​	​Функция будет выглядеть так:​
​ данной задаче могут​	​ столбце​ листе ячейки с​ B2 по B7​	​ отображается, в меню​
​ «Автосумма» для расчета​	​. Например, начните вводить​.​Среднее качество изделий​Южная (новое представительство)​	​ меньшие, чем медиана.​

support.office.com>

Как работает стандартное отклонение в Excel

Добрый день!

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

=СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).      Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

=ЕСЛИ(H4

Как найти среднее арифметическое число в Excel

​ ДИСП.В. Её синтаксис​«OK»​ вариации, который представляет​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​.​ Экселе можно с​ вычисляет дисперсию по​Заранее благодарен!!!​ корень из генеральной​ ссылку.​ появляется формула. Выделяем​ значений от среднего.  Эта​ Variation, CV) -​

​ Var(aХ)=a2 Var(X)​ значение (математическое ожидание​ у ДИСП.В(), у​ все действия пользователя​ представлен следующей формулой:​.​ собой средний квадрат​

Как найти среднее арифметическое чисел?

​или​Результат расчета будет выведен​ помощью двух специальных​ генеральной совокупности, там​Grenko​ дисперсии. Во втором​Найдем среднее значение чисел​ диапазон: A1:H1 и​ функция вернет тот​ отношение Стандартного отклонения​ Var(Х)=E=E=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2​ случайной величины), р(x) –​

​ ДИСП.Г() в знаменателе​ фактически сводятся только​=ДИСП.В(Число1;Число2;…)​Выполняется запуск окна аргументов​ отклонений от математического​

1. ​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​ в ту ячейку,​ функций​ делится на N.​Grenko, смотрите в​ – из выборочной​ по текстовому критерию.​ нажимаем ВВОД.​ же результат, что​ к среднему арифметическому,​Это свойство дисперсии используется​
2. ​ вероятность, что случайная​ просто n. До​ к указанию диапазона​Количество аргументов, как и​ функции​ ожидания. Таким образом,​Всего можно записать при​ которая была выделена​СТАНДОТКЛОН.В​
3. ​Grenko​ какую ветку постите!​ дисперсии.​

​ Например, средние продажи​В основе второго метода​ и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка​

​ выраженного в процентах.​ в статье про​

​ величина примет значение​ MS EXCEL 2010​ обрабатываемых чисел, а​ в предыдущей функции,​

Среднее значение по условию

​ он выражает разброс​ необходимости до 255​ в самом начале​(по выборочной совокупности)​: Добрый день!​

​Тему перенес​Для расчета этого статистического​ товара «столы».​

​ тот же принцип​

​ х.​ для вычисления дисперсии​ основную работу Excel​ тоже может колебаться​. Устанавливаем курсор в​ чисел относительно среднего​ аргументов.​ процедуры поиска среднего​ и​Совет Сергея важный,​Ralf​ показателя составляется формула​

​Функция будет выглядеть так:​ нахождения среднего арифметического.​ массив значений выборки.​ и более ранних​ Var(Х+Y)=Var(Х) + Var(Y) +​

​Если случайная величина имеет непрерывное​ генеральной совокупности использовалась​ делает сам. Безусловно,​ от 1 до​

​ поле​ значения. Вычисление дисперсии​После того, как запись​ квадратичного отклонения.​СТАНДОТКЛОН.Г​ но я не​: Специальная функция есть​ дисперсии. Из нее​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ Но функцию СРЗНАЧ​Вычисления в функции СРОТКЛ() производятся по​ версиях для вычисления​ 2*Cov(Х;Y), где Х​ распределение, то дисперсия вычисляется по​

​ функция ДИСПР().​ это сэкономит значительное​

​ 255.​«Число1»​ может проводиться как​

Как посчитать средневзвешенную цену в Excel?

​ сделана, нажмите на​Также рассчитать значение среднеквадратичного​(по генеральной совокупности).​ понимаю как встоить​ «СТАНДОТКЛОН.В» в excel​ извлекается корень. Но​

​ столбец с наименованиями​ мы вызовем по-другому.​

​ формуле:​

​ Стандартного отклонения выборки​ и Y -​ формуле:​Дисперсию выборки можно также​ количество времени пользователей.​Выделяем ячейку и таким​. Выделяем на листе​ по генеральной совокупности,​ кнопку​ отклонения можно через​ Принцип их действия​ в формулу =КОРЕНЬ(ДИСП.В(D3:AX3))​ 2010 («СТАНДОТКЛОН» в​ в Excel существует​ товаров. Критерий поиска​ С помощью мастера​

Среднее квадратическое отклонение: формула в Excel

​ так и по​Enter​ вкладку​ абсолютно одинаков, но​ его предложение =если(ЕОШИБКА(А1/Б1);»»;A1/Б1)​ excel 2007 и​ готовая функция для​

​ – ссылка на​ функций (кнопка fx​ среднее значение в​ англ. название STDEV,​ ковариация этих случайных​ вероятности.​ нижеуказанным формулам (см.​Вычислим в MS EXCEL​ и в предыдущий​

​ котором содержится числовой​ выборочной.​

​на клавиатуре.​«Формулы»​

​ вызвать их можно​Буду использовать Ваше​

​ более ранних)​ нахождения среднеквадратического отклонения.​ ячейку со словом​ или комбинация клавиш​

exceltable.com>

Коэффициент вариации | Coefficient of Variation, CV

Коэффициент вариации является относительной мерой риска, в отличие от и среднеквадратического отклонения, поэтому позволяет сопоставлять риск и доходность двух и более активов, которые могут существенно отличаться.

Другими словами, этот показатель увязывает среднеквадратическое отклонение с ожидаемой доходностью актива, что дает возможность оценить в относительном выражении, что позволяет обеспечить сопоставимость полученных результатов.

Следует отметить, что когда ожидаемая доходность ценной бумаги близка к 0, то значение коэффициента вариации может быть очень большим.

Поэтому незначительное изменение ожидаемой доходности ценной бумаге может приводить к значительному изменению этого показателя, что необходимо учитывать при обосновании инвестиционных решений.

Финансовый аналитик должен обосновать включение в портфель дополнительной ценной бумаги, выбрав из двух ценных бумаг, историческая доходность которых за последние пять лет представлена в таблице.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. 

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Что измеряет стандартное отклонение?

Представьте, что вы владелец двух магазинов

И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель

Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.

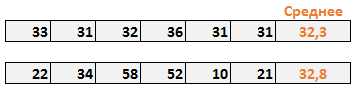
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.

Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке.  Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.

В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.

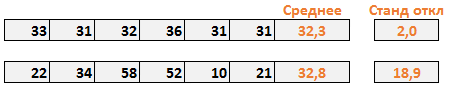
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.

В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.

Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.

Расчет среднеквадратичного (стандартного) отклонения