Формула 8: ПСТР
Эта функция дает возможность достать требуемое количество знаков с текста, начиная определенным символом по счету.
Ее синтаксис следующий:
=ПСТР(текст;начальная_позиция;число_знаков).
Расшифровка аргументов:
- Текст – это строка, в которой содержатся необходимые данные.
- Начальная позиция – это непосредственно положение того символа, который и служит началом для извлечения текста.
- Число знаков – количество символов, которые формула должна вытащить из текста.
На практике эта функция может использоваться, например, чтобы упростить названия тайтлов, убрав слова, которые находятся в их начале.
Значения функции Лапласа в Эксель
Функция Лапласа, или нормальное распределение, широко используется в статистике и математической статистике для анализа случайных процессов. Эта функция описывает распределение вероятностей случайной величины, которая может принимать любое значение в некотором интервале.
В программе Excel можно использовать формулы для вычисления значений функции Лапласа. Функция Лапласа имеет два параметра: значение случайной величины и среднее значение. Функция возвращает вероятность того, что случайная величина принимает значение меньше указанного.
Для вычисления значения функции Лапласа в Excel можно использовать формулу =НОРМ.С.ВЫШ(значение;среднее;ср.корень), где значение — искомое значение функции Лапласа, среднее — среднее значение случайной величины, а ср.корень — среднеквадратическое отклонение.
Например, для вычисления функции Лапласа для значения 2 при среднем значении 0 и среднеквадратическом отклонении 1, можно использовать формулу =НОРМ.С.ВЫШ(2;0;1), которая вернет значение вероятности.
Также в Excel доступна таблица значений функции Лапласа, которая позволяет быстро получить нужное значение без вычислений. Для этого необходимо выбрать функцию Вставка -> Таблица -> Функция -> Процент Лапласа и указать значение случайной величины и среднее значение.
Использование функции Лапласа в Excel может быть полезно при анализе данных, моделировании случайных процессов и прогнозировании вероятности наступления событий.
Функция Лапласа в Excel

Одной из самых известных неэлементарных функций, которая применяется в математике, в теории дифференциальных уравнений, в статистике и в теории вероятностей является функция Лапласа. Решение задач с ней требует существенной подготовки. Давайте выясним, как можно с помощью инструментов Excel произвести вычисление данного показателя.
Функция Лапласа
Функция Лапласа имеет широкое прикладное и теоретическое применение. Например, она довольно часто используется для решения дифференциальных уравнений. У этого термина существует ещё одно равнозначное название – интеграл вероятности. В некоторых случаях основой для решения является построение таблицы значений.
Оператор НОРМ.СТ.РАСП
В Экселе указанная задача решается с помощью оператора НОРМ.СТ.РАСП. Его название является сокращением от термина «нормальное стандартное распределение». Так как его главной задачей является возврат в выделенную ячейку стандартного нормального интегрального распределения. Данный оператор относится к статистической категории стандартных функций Excel.
В Excel 2007 и в более ранних версиях программы этот оператор назывался НОРМСТРАСП. Он в целях совместимости оставлен и в современных версиях приложений. Но все-таки в них рекомендуется использование более продвинутого аналога – НОРМ.СТ.РАСП.
Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:
Устаревший оператор НОРМСТРАСП записывается так:
Как видим, в новом варианте к существующему аргументу «Z» добавлен аргумент «Интегральная». Нужно заметить, что каждый аргумент является обязательным.
Аргумент «Z» указывает числовое значение, для которого производится построение распределения.
Аргумент «Интегральная» представляет собой логическое значение, которое может иметь представление «ИСТИНА» («1») или «ЛОЖЬ» («0»). В первом случае в указанную ячейку возвращается интегральная функция распределения, а во втором – весовая функция распределения.
Решение задачи
Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:
Теперь давайте на конкретном примере рассмотрим использование оператора НОРМ.СТ.РАСП для решения конкретной задачи.
- Выделяем ячейку, куда будет выводиться готовый результат и щелкаем по значку «Вставить функцию», расположенному около строки формул.
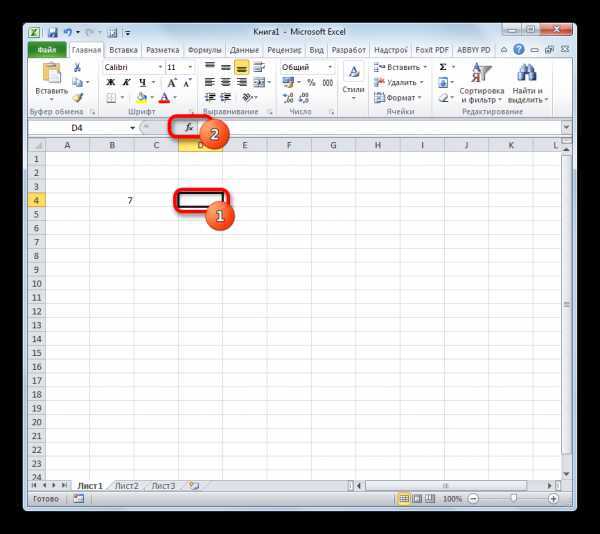
После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».
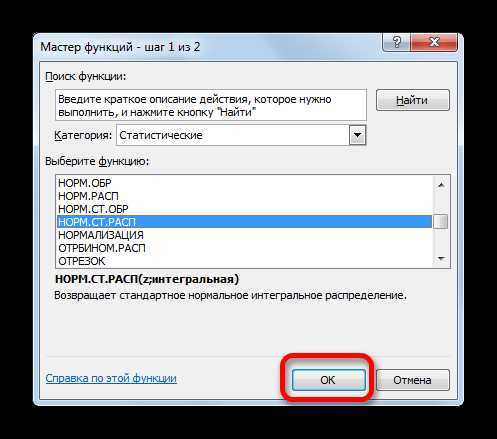
Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».
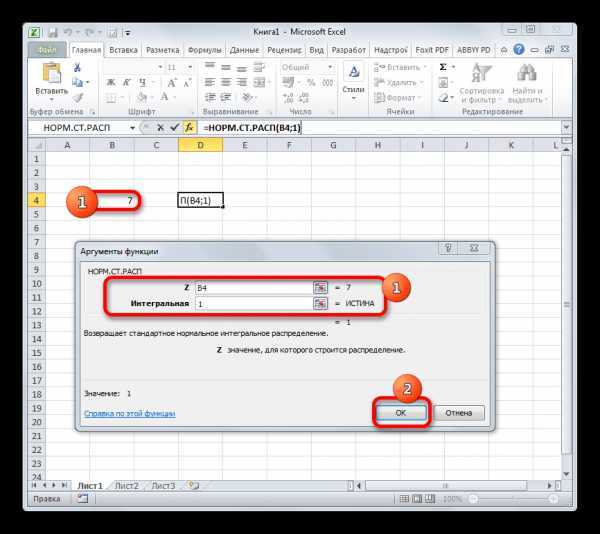
После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.
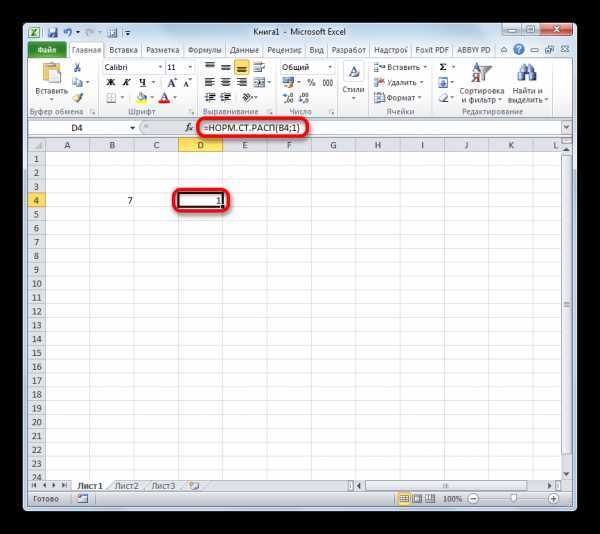
Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.
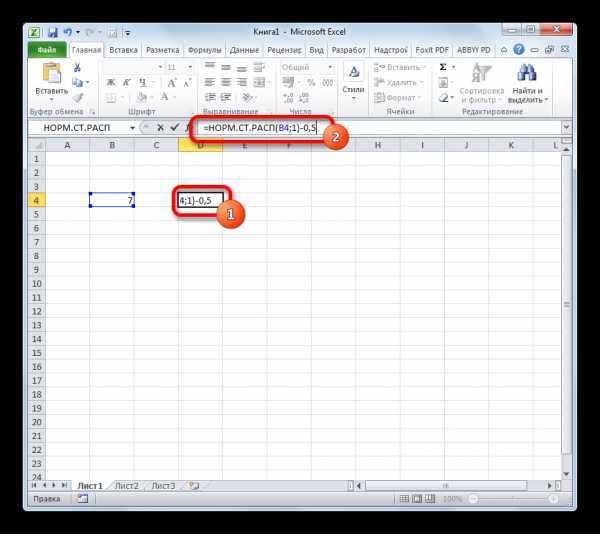
Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.
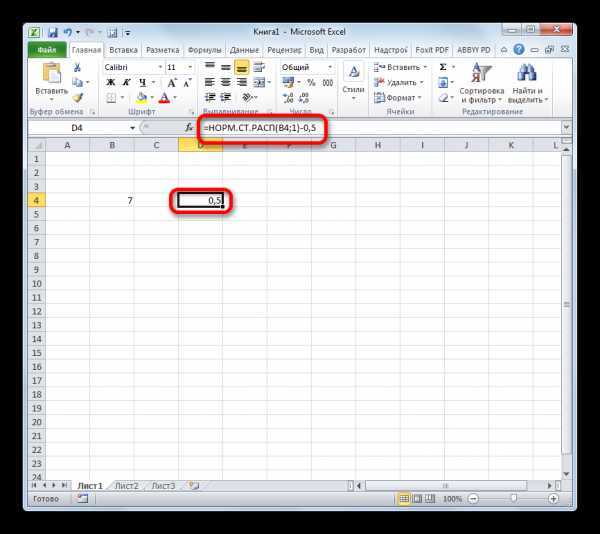
Как видим, вычислить функцию Лапласа для конкретного заданного числового значения в программе Excel не составляет особенного труда. Для этих целей применяется стандартный оператор НОРМ.СТ.РАСП.
Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Практические примеры использования функции Лапласа
- Оценка вероятности случайной величины: функция Лапласа позволяет оценить вероятность, что случайная величина примет значение в определенном диапазоне. Например, если у вас есть некоторые данные о распределении доходов населения, вы можете использовать функцию Лапласа, чтобы найти вероятность того, что доход будет находиться в определенном интервале.
- Анализ данных: функция Лапласа может быть полезна при анализе больших объемов данных. Она позволяет определить, насколько данные распределены равномерно или смещены вправо или влево. Это может быть полезно для выявления выбросов или аномалий в данных.
- Прогнозирование: функция Лапласа может быть использована для прогнозирования будущих значений на основе исторических данных. Например, если у вас есть данные о продажах вашей компании за последние несколько лет, вы можете использовать функцию Лапласа, чтобы предсказать продажи на следующий год.
- Оптимизация процессов: функция Лапласа может быть использована для оптимизации различных процессов. Например, если вы знаете, что время выполнения определенного процесса имеет нормальное распределение, вы можете использовать функцию Лапласа, чтобы определить оптимальное время выполнения этого процесса.
Это только некоторые примеры использования функции Лапласа в Excel. Она может быть полезна во многих других сферах анализа данных и математического моделирования.
Построение доверительного интервала
Обычно, зная распределение и его параметры, мы можем вычислить вероятность того, что случайная величина примет значение из заданного нами интервала. Сейчас поступим наоборот: найдем интервал, в который случайная величина попадет с заданной вероятностью. Например, из свойств нормального распределения
известно, что с вероятностью 95%, случайная величина, распределенная по нормальному закону
, попадет в интервал примерно +/- 2 от среднего значения
(см. статью про ). Этот интервал, послужит нам прототипом для доверительного интервала
.
Теперь разберемся,знаем ли мы распределение,
чтобы вычислить этот интервал? Для ответа на вопрос мы должны указать форму распределения и его параметры.
Форму распределения мы знаем – это нормальное распределение
(напомним, что речь идет о выборочном распределении
статистики
Х ср
).
Параметр μ нам неизвестен (его как раз нужно оценить с помощью доверительного интервала
), но у нас есть его оценка Х ср,
вычисленная на основе выборки,
которую можно использовать.
Второй параметр – стандартное отклонение выборочного среднего
будем считать известным
, он равен σ/√n.
Т.к. мы не знаем μ, то будем строить интервал +/- 2 стандартных отклонения
не от среднего значения
, а от известной его оценки Х ср
. Т.е. при расчете доверительного интервала
мы НЕ будем считать, что Х ср
попадет в интервал +/- 2 стандартных отклонения
от μ с вероятностью 95%, а будем считать, что интервал +/- 2 стандартных отклонения
от Х ср
с вероятностью 95% накроет μ – среднее генеральной совокупности,
из которого взята выборка
. Эти два утверждения эквивалентны, но второе утверждение нам позволяет построить доверительный интервал
.
Кроме того, уточним интервал: случайная величина, распределенная по нормальному закону
, с вероятностью 95% попадает в интервал +/- 1,960 стандартных отклонений,
а не+/- 2 стандартных отклонения
. Это можно рассчитать с помощью формулы =НОРМ.СТ.ОБР((1+0,95)/2)
, см. файл примера Лист Интервал
.
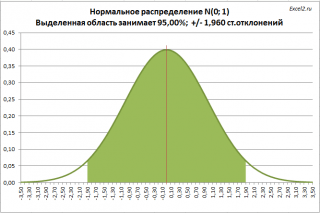
Теперь мы можем сформулировать вероятностное утверждение, которое послужит нам для формирования доверительного интервала
: «Вероятность того, что среднее генеральной совокупности
находится от среднего выборки
в пределах 1,960 «стандартных отклонений выборочного среднего»
, равна 95%».
Значение вероятности, упомянутое в утверждении, имеет специальное название , который связан с
уровнем значимости α (альфа) простым выражением уровень доверия
=1
-α.
В нашем случае уровень значимости
α=1-0,95=0,05
.
Теперь на основе этого вероятностного утверждения запишем выражение для вычисления доверительного интервала
:
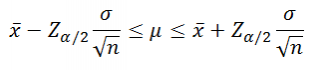
где Z α/2
–
стандартного
нормального распределения
(такое значение случайной величины z
,
что P
(z
>=Z α/2
)=α/2
).
Примечание
: Верхний α/2-квантиль
определяет ширину доверительного интервала
в стандартных отклонениях
выборочного среднего. Верхний α/2-квантиль
стандартного
нормального распределения
всегда больше 0, что очень удобно.
В нашем случае при α=0,05, верхний α/2-квантиль
равен 1,960. Для других уровней значимости α (10%; 1%) верхний α/2-квантиль
Z α/2
можно вычислить с помощью формулы =НОРМ.СТ.ОБР(1-α/2)
или, если известен уровень доверия
, =НОРМ.СТ.ОБР((1+ур.доверия)/2)
.
Обычно при построении доверительных интервалов для оценки среднего
используют только верхний α
/2-квантиль
и не используют нижний α
/2-квантиль
. Это возможно потому, что стандартное
нормальное распределение
симметрично относительно оси х (плотность его распределения
симметрична относительно среднего, т.е. 0
).
Поэтому, нет нужды вычислять нижний α/2-квантиль
(его называют просто α/2-квантиль
), т.к. он равен верхнему α
/2-квантилю
со знаком минус.
Напомним, что, не смотря на форму распределения величины х, соответствующая случайная величина Х ср
распределена приблизительно
нормально
N(μ;σ 2 /n) (см. статью про ). Следовательно, в общем случае, вышеуказанное выражение для доверительного интервала
является лишь приближенным. Если величина х распределена по нормальному закону
N(μ;σ 2 /n), то выражение для доверительного интервала
является точным.
Как вычислить неберущийся интеграл с помощью Вольфрам Альфа
Эта статья о том, как вычислить неберущийся интеграл онлайн, содержит примеры вычисления неберущихся интегралов с помощью Вольфрам Альфа.
Здесь продолжена тема, которая рассматривалась в статьях Определенный интеграл в Wolfram|Alpha, Как вычислить приближенное значение определенного интеграла в Wolfram|Alpha, используя численные методы решения интегралов, Численное интегрирование в Wolfram|Alpha, и рассмотрены основные способы вычисления неберущихся интегралов в системе Вольфрам Альфа.
Вычислить интеграл — так говорят об определенном интеграле, поскольку определенный интеграл, по его определению, есть число, которое «вычисляется», в отличие от неопределенного интеграла, который есть переменная величина, и поэтому «находится». Что же такое «неберущийся» интеграл? Так называют неопределенные интегралы, которые не выражаются через элементарные функции. То есть, это интегралы, в которых первообразную подынтегральной функции нельзя найти легко и быстро. Найти-то ее в принципе можно, но лень. Или же не хватает времени, знаний… Тогда и говорят, что первообразная не существует, и интеграл неберущийся. Определенные интегралы также называют неберущимися, когда определенный интеграл существует, как предел интегральной суммы, но подынтегральная функция не имеет первообразной, либо когда первообразная подынтегральной функции не выражается через элементарные функции.
Таким образом, различают, когда определенный интеграл, как предел интегральной суммы, в принципе существует, но «не берется», и когда определенный интеграл не существует в принципе. Примеры можно также найти в статье Несобственные интегралы в Wolfram|Alpha.
Вот простой пример неберущегося интеграла:
integrate e^(x^2), x=0..1
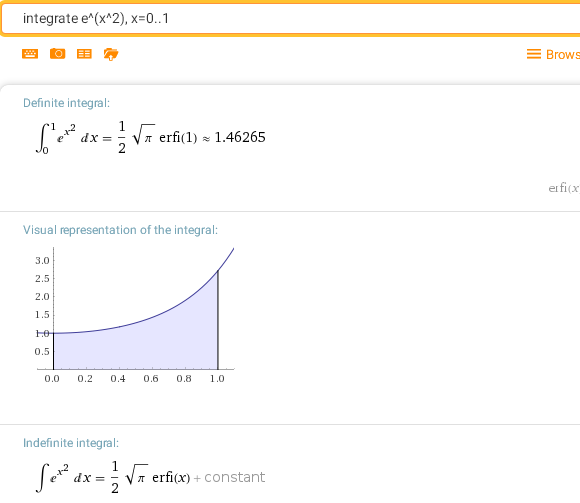
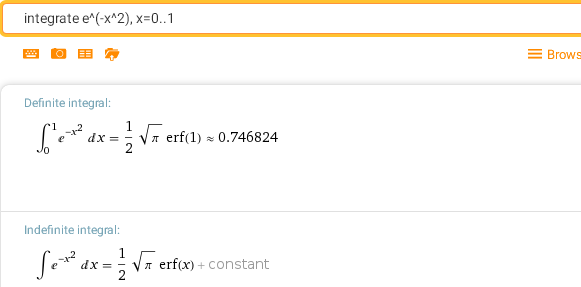
Здесь erf(x) — функция ошибок (интеграл вероятностей), неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Другие типичные примеры неберущихся интегралов, которые находят применение в физике, точнее, в оптике:
integrate sin(x^2), x=0..1
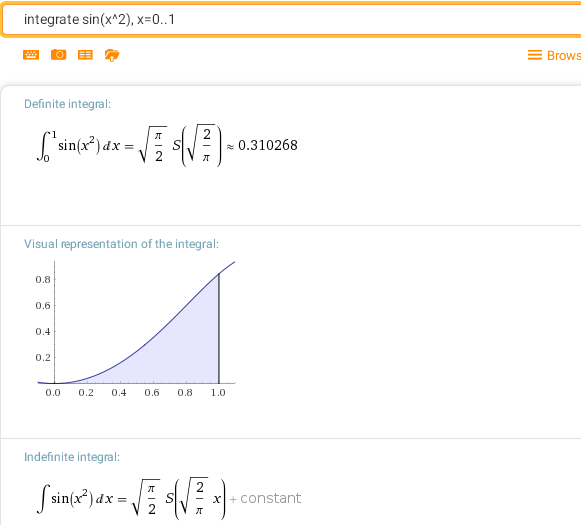
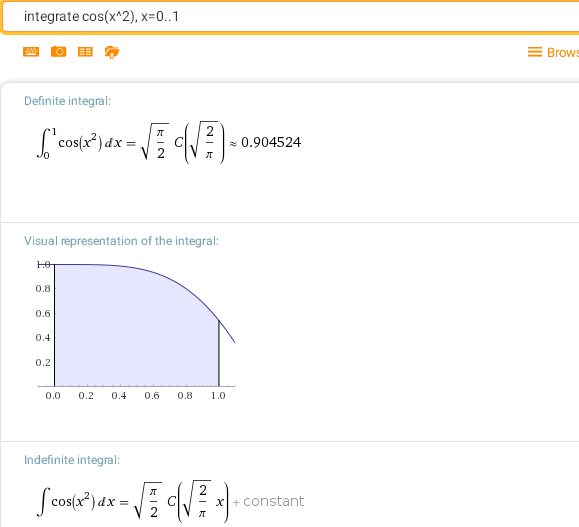
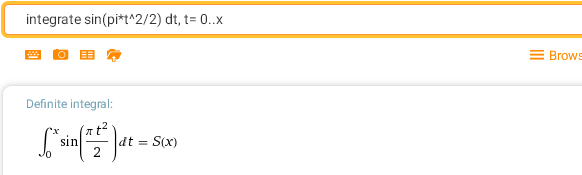
integrate cos(pi*t^2/2) dt, t= 0..x — C-интеграл Френеля
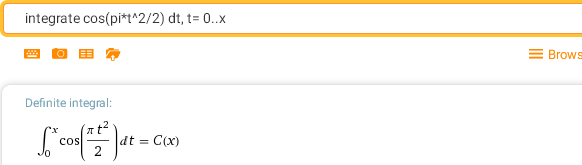 |
К таким же не элементарным функциям относятся Ci(x) — интегральный косинус, Si(x) — интегральный синус, li(x) — интегральный логарифм, соответственно:
integrate -cos(t)/t, t= x..inf — интегральный косинус 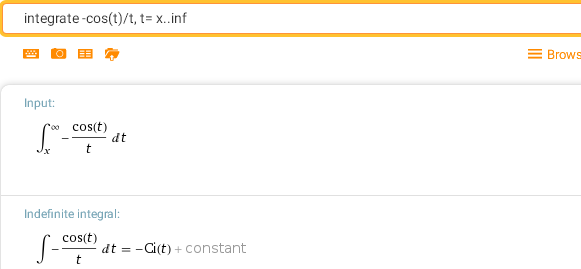
integrate sin(t)/t, t= 0..x — интегральный синус 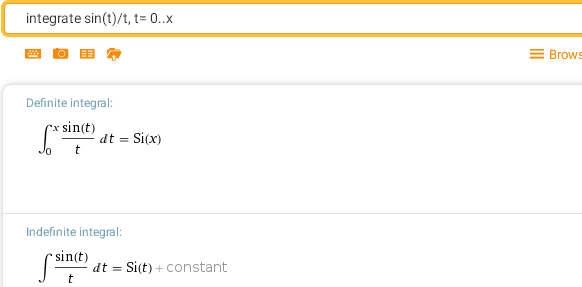
integrate 1/ln(t), t= 0..x — интегральный логарифм 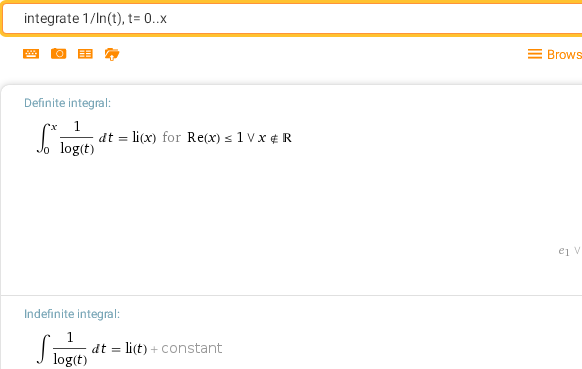
Соответственно, через эти функции выражаются такие интегралы, как
integrate cos(x)/x, x= 1..inf 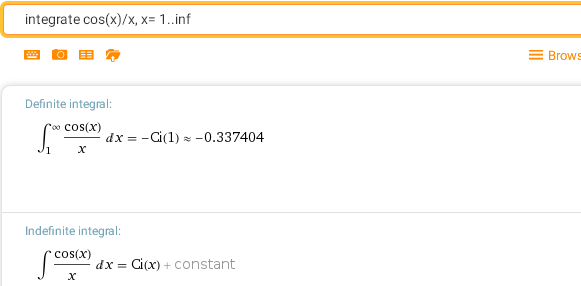
integrate sin(x)/x, x= 0..1
Последний интеграл также неберущийся. Он выражается через эллиптический интеграл второго рода E(x).
Однако, из правила всеядности Вольфрам Альфа существуют исключения. Вот почему, когда используете Вольфрам Альфа, все же лучше строго соблюдать правила математической нотации. Например,
integrate sqrt(1-sin(x^2)/4), x=0..pi
Кстати, этот последний интеграл, который, как и предыдущие, тоже является «неберущимся». Но при этом он не выражается даже через неэлементарные функции. В этом легко убедится непосредственно, найдя неопределенный интеграл, который, как видим, представляется в виде степенного ряда:
integrate sqrt(1-sin(x^2)/4)
integrate 1/ln(x), x= -1..3
integrate 1/ln(x), x= -1..0
Локальная теорема Лапласа
Если вероятность появления случайного события в каждом испытании постоянна, то вероятность того, что в испытаниях событие наступит ровно раз, приближённо равна: , где .
При этом, чем больше , тем рассчитанная вероятность будет лучше приближать точное значению , полученное (хотя бы гипотетически)
по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность ближе к 0,5, и наоборот – даёт существенную погрешность при значениях , близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы является выполнение неравенства ()
.
Так, например, если , то и применение теоремы Лапласа для 50 испытаний оправдано. Но если и , то и приближение (к точному значению )
будет плохим.
О том, почему и об особенной функции мы поговорим на уроке о нормальном распределении вероятностей
, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность
этой функции: .
Оформим официальные отношения с нашим примером:
Задача 1
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно:
а) 200 раз;
б) 225 раз.
С чего начать решение
? Сначала распишем известные величины, чтобы они были перед глазами:
– общее количество независимых испытаний; – вероятность выпадения орла в каждом броске; – вероятность выпадения решки.
а) Найдём вероятность того, что в серии из 400 бросков орёл выпадет ровно раз. Ввиду большого количества испытаний используем локальную теорему Лапласа: , где .
На первом шаге вычислим требуемое значение аргумента:
Далее находим соответствующее значение функции: . Это можно сделать несколькими способами. В первую очередь, конечно же, напрашиваются непосредственные вычисления:
Округление проводят, как правило, до 4 знаков после запятой.
Недостаток прямого вычисления состоит в том, что экспоненту переваривает далеко не каждый микрокалькулятор, кроме того, расчёты не особо приятны и отнимают время. Зачем так мучиться? Используйте калькулятор по терверу
(пункт 4)
и получайте значения моментально!
Кроме того, существует таблица значений функции
, которая есть практически в любой книге по теории вероятностей, в частности, в учебном пособии В.Е. Гмурмана
. Закачайте, кто ещё не закачал – там вообще много полезного;-) И обязательно научитесь пользовать таблицей (прямо сейчас!)
– подходящей вычислительной техники всегда может не оказаться под рукой!
На заключительном этапе применим формулу : – вероятность того, что при 400 бросках монеты орёл выпадет ровно 200 раз.
Как видите, полученный результат очень близок к точному значению , вычисленному по формуле Бернулли
.
б) Найдём вероятность того, что в серии из 400 испытаний орёл выпадет ровно раз. Используем локальную теорему Лапласа. Раз, два, три – и готово:
– искомая вероятность.
Ответ
:
Следующий пример, как многие догадались, посвящён деторождению – и это вам для самостоятельного решения:)
Задача 2
Вероятность рождения мальчика равна 0,52. Найти вероятность того, что среди 100 новорожденных окажется ровно: а) 40 мальчиков, б) 50 мальчиков, в) 30 девочек.
Результаты округлить до 4 знаков после запятой.
…Интересно тут звучит словосочетание «независимые испытания» =) Кстати, реальная статистическая вероятность
рождения мальчика во многих регионах мира колеблется в пределах от 0,51 до 0,52.
Примерный образец оформления задачи в конце урока.
Все заметили, что числа получаются достаточно малыми, и это не должно вводить в заблуждение – ведь речь идёт о вероятностях отдельно взятых, локальных
значениях (отсюда и название теоремы). А таковых значений много, и, образно говоря, вероятности «должно хватить на всех». Правда, многие события будут практически невозможными
.
Поясню вышесказанное на примере с монетами: в серии из четырёхсот испытаний орёл теоретически может выпасть от 0 до 400 раз, и данные события образуют полную группу
:
Однако бОльшая часть этих значений представляет собой сущий мизер, так, например, вероятность того, что орёл выпадет 250 раз – уже одна десятимиллионная: . О значениях наподобие тактично умолчим =)
С другой стороны, не следует недооценивать и скромные результаты: если составляет всего около , то вероятность того, орёл выпадет, скажем, от 220 до 250 раз
, будет весьма заметна.
А теперь задумаемся: как вычислить данную вероятность? Не считать же по теореме сложения вероятностей несовместных событий
сумму:
Гораздо проще эти значения объединить
. А объединение чего-либо, как вы знаете, называется интегрированием
:
Функции даты и времени
Данный раздел формул очень интересен и полезен. При помощи их можно проводить быстрый анализ какой-нибудь информации либо вытаскивать определенные данные из указанной даты.
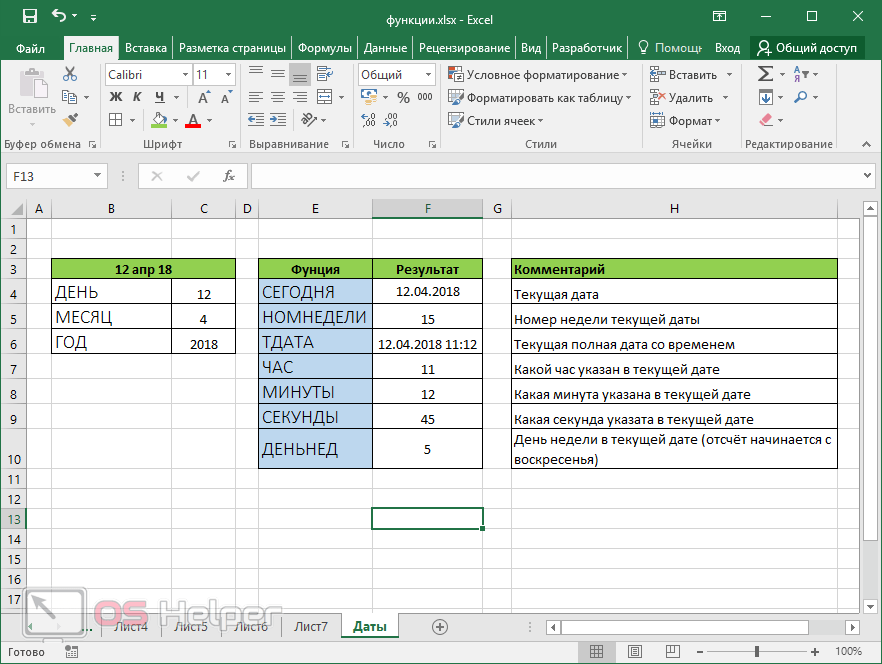
- ДЕНЬ – определяется день в указанной дате;
- МЕСЯЦ – определяется месяц в указанной дате;
- ГОД – определяется год в указанной дате;
- СЕГОДНЯ – вывод текущей даты;
- НОМНЕДЕЛИ – вывод номера недели на основании указанной даты;
- ТДАТА – вывод текущей даты и текущего времени;
- ЧАС – определяется какой час указан в определенной дате;
- МИНУТЫ – определяется сколько минут указано в определенной дате;
- СЕКУНДЫ – определяется сколько секунд указано в определенной дате;
- ДЕНЬНЕД – вычисляется порядковый номер дня недели (отсчет начинается с воскресенья, а не с понедельника).
Кроме этого, есть и более сложные формулы. К ним относятся:
- РАЗНДАТ – происходит расчет количества лет, месяцев и дней между указанными датами;
- ДНИ – происходит расчет количества дней между указанными датами (функция появилась в 2013 году);
- ЧИСТРАБДНИ – происходит расчет количества рабочих дней между указанными датами;
- ДЕНЬНЕД – преобразование обычной даты в числовом формате в порядковый номер недели;
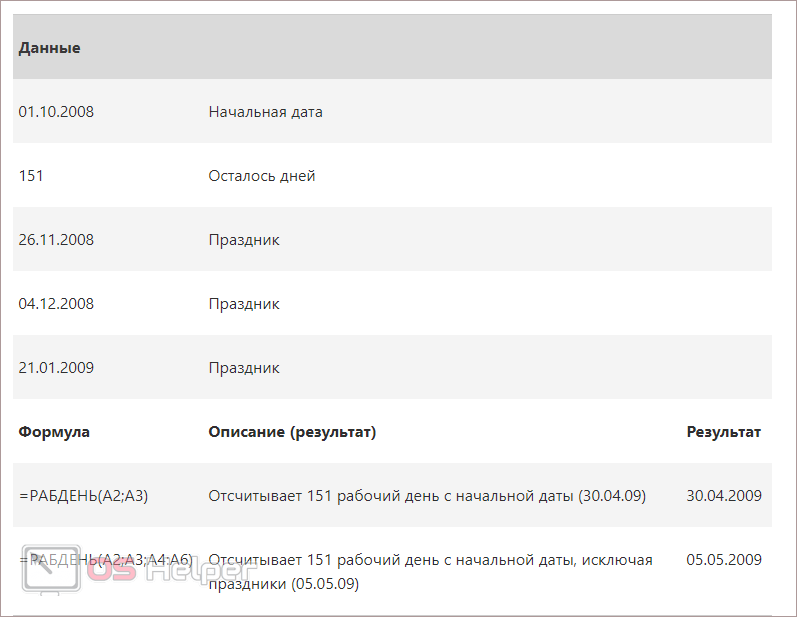
- РАБДЕНЬ – вывод даты, которая отстает или опережает указанное количество дней.
Более подробно о последней формуле можно прочитать на Microsoft.
Синтаксис данной функции следующий.

А примеры довольно простые.
О «неберущихся» интегралах
специальныминеберущимисяне берётся
Пример 1.8 Неберущимся является интеграл
Здесь одна из первообразных, которую мы обозначили , выделяется из всего набора первообразных условием . Функция называется функцией Лапласа. Она широко применяется в теории вероятностей, физике, математической и прикладной статистике и других разделах науки и её приложений. Для вычисления значений функции Лапласа составлены таблицы, имеющиеся во многих учебниках, задачниках и справочниках по теории вероятностей и статистике. Возможность вычисления предусмотрена также на многих моделях калькуляторов (не самых дешёвых) и уж, обязательно, на тех, что предназначены для статистической обработки числового материала. Так что, с практической точки зрения, пользоваться функцией Лапласа ничуть не сложнее, чем, скажем, синусом, арктангенсом или натуральным логарифмом, которые мы условно относим к элементарным функциям.
Пример 1.9 Не берётся также интеграл
Доопределим подынтегральную функцию , полагая её равной 1 при . В соответствии с тем, что , доопределённая функция будет непрерывна на всей числовой оси. Среди её первообразных выделим ту, для которой . Эта неэлементарная функция называется интегральным синусом и обозначается . Именно её мы использовали в приведённой выше формуле.
Пример 1.10 Ещё один неберущийся интеграл:
Одна из первообразных — та, что мы использовали в правой части и обозначили — называется интегральным косинусом.
Пример 1.11
—
это тоже неберущийся интеграл. Одна из первообразных, которую мы обозначили , — специальная функция, называющаяся интегральной экспонентой.
Пример 1.12 Не берётся интеграл
(при
одна из первообразных, , называется интегральным логарифмом.
Используя специальные функции, заданные предыдущими примерами, мы с помощью изученных выше правил интегрирования можем выражать через эти функции и другие интегралы. Приведём такой пример.
Пример 1.13 Выразим через функцию Лапласа следующий интеграл:
Для этого сделаем замену переменного :
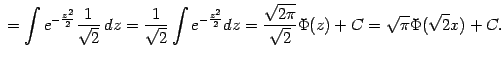 |
Заметим, что та первообразная для , для которой , обозначается . Функция называется в теории вероятностей и статистике функцией ошибок.
Упражнение 1.3 Выразите функцию ошибок через функцию Лапласа и наоборот, функцию Лапласа через функцию ошибок.
Пример 1.14 К интегралу предыдущего примера можно свести и тем самым выразить через функцию Лапласа, например, такой интеграл:
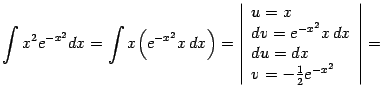 |
|
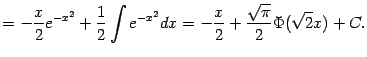 |
Для вычисления мы применили формулу интегрирования по частям.
Пример 1.15 Вычислим интеграл от интегральной экспоненты . Заметим, что по определению первообразной. Применяя формулу интегрирования по частям, получаем:
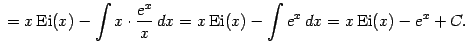 |
Кроме приведённых выше, в приложениях встречаются и многие другие неберущиеся интегралы, например:
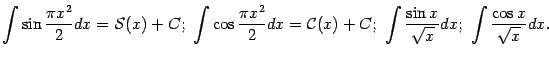
интегралами Френеля
Упражнение 1.4 Сделав соответствующую замену переменного, выразите последние два из интегралов Френеля через функции и , которые стоят в правых частях первых двух интегралов Френеля.
Не берутся также интегралы
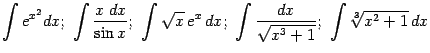
Тем не менее, для многих классов интегралов, наиболее часто встречающихся в приложениях, первообразную всё же удаётся выразить через элементарные функции. В следующей главе мы изучим такие классы интегралов.
Упражнение 1.5 С помощью соответствующих замен переменного, докажите следующие соотношения:
(при (при
(на самом деле функции и определяются так, что обе постоянные равны 0).
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

























