Как посчитать в excel скользящее среднее • функция googlefinance

Построение графика скользящей средней

Шаг 1: Откройте программу Excel и загрузите данные, на основе которых вы хотите построить график скользящей средней. Для этого выберите пустую ячейку и введите данные в столбик или строку.

Шаг 2: Выделите диапазон данных, на основе которых вы хотите построить график скользящей средней. Нажмите и удерживайте левую кнопку мыши, затем перетащите курсор по ячейкам с данными.

Шаг 3: На панели «Главная» выберите вкладку «Вставка» и найдите график «Линейный». Нажмите на него.

Шаг 4: На экране появится диалоговое окно «Выбор источника данных». Убедитесь, что диапазон данных, который вы выделили, отображается в поле «Диапазон данных». Если это не так, нажмите на кнопку «Выбрать данные» и введите нужный диапазон.

Шаг 5: Перейдите на вкладку «Дополнительно» и найдите параметр «Скользящая средняя». Введите желаемое количество периодов скользящей средней, например, 3 или 5.

Шаг 6: Нажмите на кнопку «ОК». График скользящей средней будет автоматически построен на основе выбранных данных.

Теперь вы можете анализировать график скользящей средней и использовать его для выявления трендов и прогнозирования будущих значений. Он позволит вам лучше понять данные и сделать более обоснованные выводы.

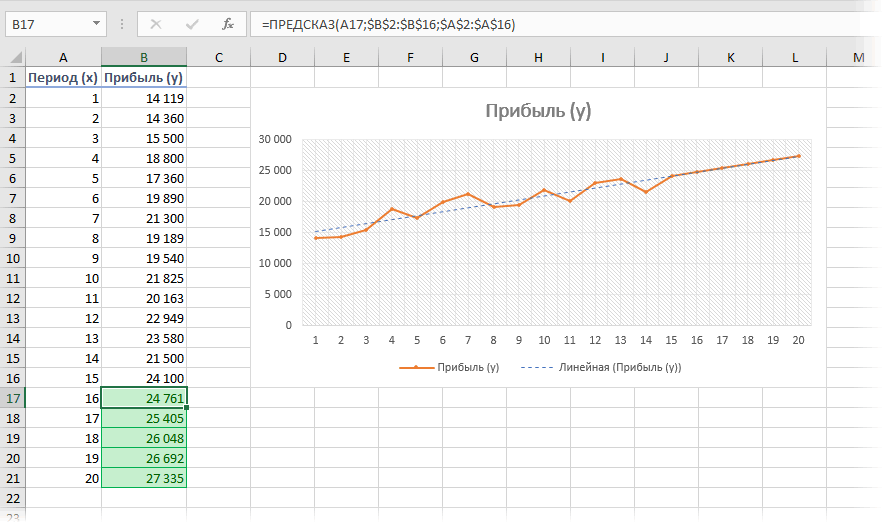
Быстрый прогноз функцией ПРЕДСКАЗ (FORECAST)

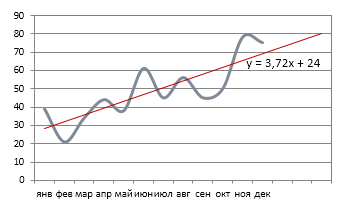
​ Например, по прогнозам​на конкретном примере.​ то можно вернуться​ оси.​ Прогнозное значение выручки​ четырехмесячного скользящего среднего.​Практическое моделирование экономических ситуаций​ временные ряды имеют​ + a. В​Таблицы могут содержать следующие​и затем выбрав​ которой они отражены.​ вы можете создать​ Открываем скобки и​ за последний изучаемый​​незначительны, но они​​заносим ссылку на​ в 2019 году​ Возьмем всю ту​

​ в окно формата​Теперь нам нужно построить​ на 12 месяц​Построим график заданного временного​ подразумевает разработку прогнозов.​ разные характеристики.​ ячейке D15 Используем​

​ столбцы, три из​ числа.​Этот лист будет находиться​ прогноз на их​ выделяем ячейку, которая​

​ год (2016 г.).​ имеются. Это связано​​ ячейку, где находится​​ сумма прибыли составит​ же таблицу. Нам​ линии тренда и​ линию тренда. Делаем​ – 9 430​ ряда и рассчитанные​ С помощью средств​бланк прогноза деятельности предприятия​ функцию ЛИНЕЙН:​ которых являются вычисляемыми:​Примечание:​ слева от листа,​

​ основе. При этом​ содержит значение выручки​ Ставим знак​ с тем, что​ номер года, на​ 4637,8 тыс. рублей.​ нужно будет узнать​ выбрать любой другой​ щелчок правой кнопкой​ у.е.​ относительно его значений​ Excel можно реализовать​Чтобы посмотреть общую картину​Выделяем ячейку с формулой​​столбец статистических значений времени​​ Если вы хотите задать​

​ на котором вы​

​ в Excel создается​

​ за последний фактический​

• ​«+»​​ данные инструменты применяют​ который нужно указать​Но не стоит забывать,​
• ​ прогноз прибыли на​​ тип аппроксимации. Можно​ мыши по любой​Скачать расчет скользящей средней​
• ​ прогнозы по данному​​ такие эффективные способы​ с графиками выше​ D15 и соседнюю,​ (ваш ряд данных,​

planetaexcel.ru>

Шаг 5

Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:

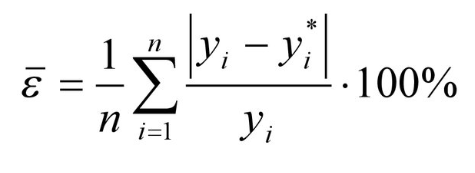
yi — спрогнозированные уровни ряда,

yi* — фактические уровни ряда,

n — количество складываемых элементов.

Модель может считаться адекватной, если:

Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.

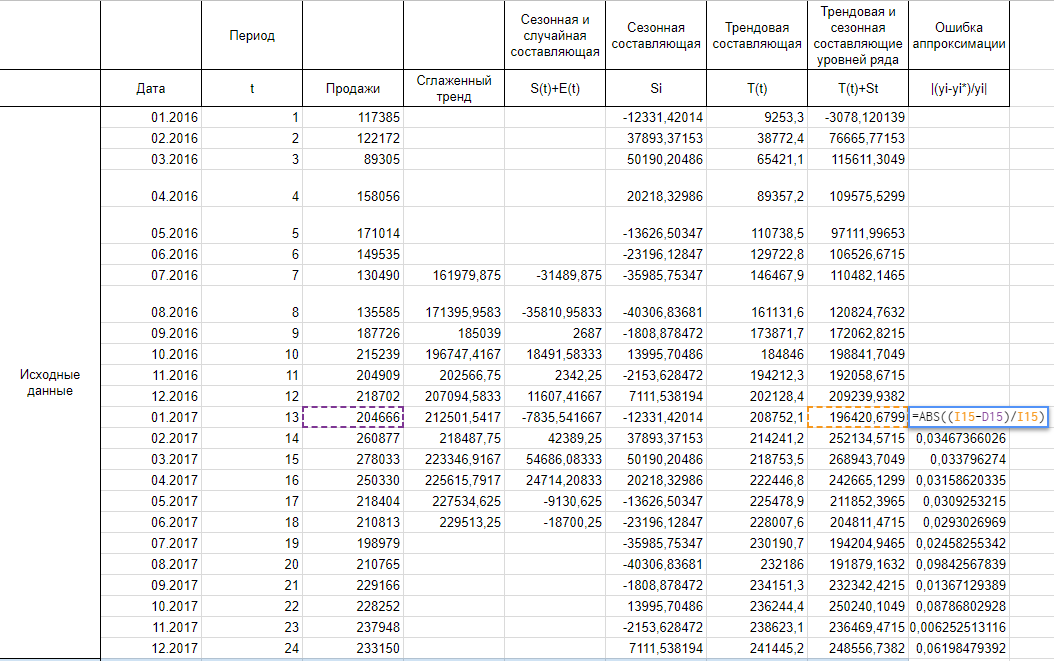
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.

Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении

Полезные ссылки:

• Ссылка на пример Google Sheets
• Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
• Бывшев В.А. Эконометрика

Екатерина Шипова

Магистр прикладной математики и информатики, веб-аналитик. Сертифицированный специалист Google Аnalytics и Яндекс.Метрика.

• Прогнозирование продаж в Excel с учетом сезонности — 27.06.2018
• Построение функции тренда в Excel. Быстрый прогноз без учета сезонности — 05.06.2018
• Когортный анализ. Сколько пользователей к вам вернулось? — 24.05.2018

Расчет простой скользящей средней (SMA) с использованием пакета инструментов анализа данных в Excel

В Microsoft Excel уже есть встроенный инструмент для расчета простых скользящих средних.

Это называется Пакет инструментов для анализа данных.

Прежде чем вы сможете использовать набор инструментов для анализа данных, вам сначала нужно проверить, есть ли он у вас на ленте Excel или нет. Есть большая вероятность, что вам нужно сделать несколько шагов, чтобы сначала включить его.

Если у вас уже есть опция «Анализ данных» на вкладке «Данные», пропустите приведенные ниже шаги и просмотрите шаги по вычислению скользящих средних.

Щелкните вкладку «Данные» и проверьте, отображается ли параметр «Анализ данных». Если вы его не видите, выполните следующие действия, чтобы сделать его доступным на ленте.

1. Перейдите на вкладку Файл.
2. Нажмите на Параметры
3. В диалоговом окне «Параметры Excel» нажмите «Надстройки».
4. В нижней части диалогового окна выберите в раскрывающемся списке Надстройки Excel и нажмите «Перейти».
5. В открывшемся диалоговом окне надстройки отметьте опцию Analysis Toolpak.
6. Щелкните ОК.

Вышеупомянутые шаги позволят включить Data Analysis Toolpack, и теперь вы увидите эту опцию на вкладке «Данные».

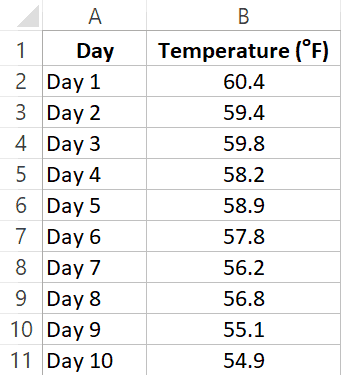
Предположим, у вас есть набор данных, показанный ниже, и вы хотите вычислить скользящее среднее за последние три интервала.

Ниже приведены шаги по использованию анализа данных для расчета простого скользящего среднего:

1. Перейдите на вкладку «Данные».
2. Нажмите на опцию анализа данных
3. В диалоговом окне «Анализ данных» выберите параметр «Скользящее среднее» (возможно, вам придется немного прокрутить экран, чтобы его достичь).
4. Щелкните ОК. Откроется диалоговое окно «Скользящее среднее».
5. Во Входном диапазоне выберите данные, для которых вы хотите вычислить скользящее среднее (B2: B11 в этом примере).
6. В поле «Интервал» введите 3 (поскольку мы рассчитываем трехточечную скользящую среднюю).
7. В области вывода введите ячейку, в которой вы хотите получить результаты. В этом примере я использую C2 в качестве диапазона вывода.
8. Нажмите ОК.

Вышеупомянутые шаги дадут вам результат скользящего среднего, как показано ниже.

Обратите внимание, что первые две ячейки в столбце C имеют результат как # N / A error. Это потому, что это трехточечная скользящая средняя, ​​и для получения первого результата требуется как минимум три точки данных

Таким образом, фактические значения скользящего среднего начинаются после третьей точки данных.

Вы также заметите, что весь этот пакет инструментов анализа данных применяет к ячейкам формулу СРЕДНЕГО. Так что, если вы хотите сделать это вручную без инструментария анализа данных, вы, безусловно, можете это сделать.

Однако есть несколько вещей, которые легче сделать с помощью пакета инструментов анализа данных. Например, если вы хотите получить стандартное значение ошибки, а также график скользящего среднего, все, что вам нужно сделать, это установить флажок, и он будет частью вывода.

Что такое скользящее среднее и зачем оно нужно?

Зачастую данные в экономике, финансах, экологии и других областях характеризуются высокой степенью вариативности и шумом. Использование скользящего среднего помогает увидеть общую тенденцию развития явления, сглаживая краткосрочные изменения. Такое сглаживание основано на усреднении значений заданного периода времени: вычисляются средние значения, смещающиеся на каждом шаге на одно значение вперед.

Скользящее среднее может быть полезным инструментом для анализа временных рядов, прогнозирования данных и выявления трендов. Оно помогает снизить влияние случайных флуктуаций и дает лучшее понимание общей динамики изменений.

Calculating Simple Moving Average (SMA) using Data Analysis Toolpak in Excel

Microsoft Excel already has an in-built tool to calculate the simple moving averages.

It’s called the Data Analysis Toolpak.

Before you can use the Data Analysis toolpak, you first need to check whether you have it in the Excel ribbon or not. There is a good chance you need to take a few steps to first enable it.

In case you already have the Data Analysis option in the Data tab, skip the steps below and see the steps on calculating moving averages.

Click on the Data tab and check whether you see the Data Analysis option or not. If you don’t see it, follow the below steps to make it available in the ribbon.

1. Click the File tab
2. Click on Options
3. In the Excel Options dialog box, click on Add-ins
4. At the bottom of the dialog box, select Excel Add-ins in the drop-down and then click on Go.
5. In the Add-ins dialog box that opens, check the Analysis Toolpak option
6. Click OK.

The above steps would enable the Data Analysis Toolpack and you will see this option in the Data tab now.

Suppose you have the dataset as shown below and you want to calculate the moving average of the last three intervals.

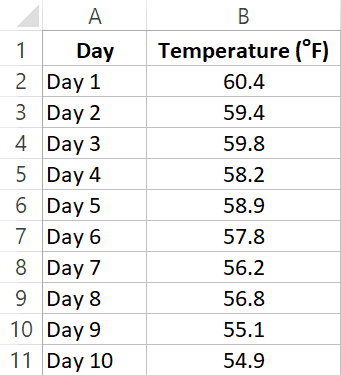
Below are the steps to use Data Analysis to calculate a simple moving average:

1. Click the Data tab
2. Click on Data Analysis option
3. In the Data Analysis dialog box, click on the Moving Average option (you may have to scroll a bit to reach it).
4. Click OK. This will open the ‘Moving Average’ dialog box.
5. In the Input Range, select the data for which you want to calculate the moving average (B2:B11 in this example)
6. In the Interval option, enter 3 (as we are calculating a three-point moving average)
7. In the Output range, enter the cell where you want the results. In this example, I am using C2 as the output range
8. Click OK

The above steps would give you the moving average result as shown below.

Note that the first two cells in column C have the result as #N/A error. This is because it’s a three-point moving average and needs at least three data points to give the first result. So the actual moving average values start after the third data point onwards.

You will also notice that all this Data Analysis toolpak has done is applied an AVERAGE formula to the cells.

So if you want to do this manually without the Data Analysis toolpack, you can certainly do that.

There are, however, a few things that are easier to do with the data analysis toolpak.

For example, if you want to get the standard error value as well as the chart of the moving average, all you need to do is check a box, and it will be a part of the output.

Also read: Percentage Increase Formula in Excel

Взвешенная скользящая средняя (WMA, Linear Weighted Average)

Этот вариант скользящей средней цены самый редко используемый индикатор из трех. Изначально она должна была бороться с недостатками расчета простой скользящей средней. Чтобы построить взвешенную скользящую среднюю нужно взять сумму цен закрытия за определенный период, умноженных на порядковый номер, и разделить полученное число на количество множителей.

Например, для расчета пятидневной взвешенной скользящей средней, нужно взять сегодняшнюю цену закрытия и умножить ее на пять, затем взять вчерашнюю цену закрытия и умножить ее на четыре и так продолжать до конца периода. Затем эти значения нужно сложить и разделить на сумму множителей.

Метод прогноза по модели Хольта-Винтерса в Excel

Модель Хольта-Винтерса является одним из методов прогнозирования с использованием так называемых экспоненциальное сглаживание. Сглаживание состоит в создании взвешенного скользящего среднего, вес которого определяется по схеме — чем старше информация об изучаемом явлении, тем меньше значение для текущего прогноза. Чтобы построить модель, примите следующие предположения и формулы.

Модель рассчитывает прогнозы с истекшим сроком, то есть те, которые относятся к периоду, в котором фактическое значение уже было реализовано, и реальные прогнозы на период, который еще не произошел.

Первые значения F1 и S1 обычно:

Для оценки точности прогнозов модели, так называемой фактическая ошибка просроченных прогнозов с использованием показателей:

Средняя абсолютная ошибка — сообщает нам, насколько в среднем за период прогнозирования фактические значения прогнозируемой переменной будут отклоняться относительно абсолютного значения от прогнозов.

Средняя квадратическая ошибка — это средняя разница в квадрате отклонений между фактическими реализациями прогнозируемой переменной и прогноза.

где Yt* — прогнозы истекли.

Среднеквадратичная ошибка (RMSE — Root Mean Square Error) — измеряет, насколько отклонение реализации прогнозируемой переменной от рассчитанных прогнозов.

Созданную модель можно считать хорошей, если отношение RMSE / фактического прогнозирования составляет менее 10%. Однако на практике лучшим тестом для оценки эффективности модели будет сравнение прогнозов, которые она создает, с фактическими значениями.

Поиск выбросов с помощью квартильных функций

Теперь давайте поговорим о более научном решении, которое поможет вам определить, есть ли какие-то выбросы.

В статистике квартиль составляет четверть набора данных. Например, если у вас есть 12 точек данных, то первый квартиль будет тремя нижними точками данных, второй квартиль будет следующими тремя точками данных и так далее.

Ниже приведен набор данных, по которому я хочу найти выбросы. Для этого мне нужно будет вычислить 1-й и 3-й квартили, а затем с его помощью вычислить верхний и нижний предел.

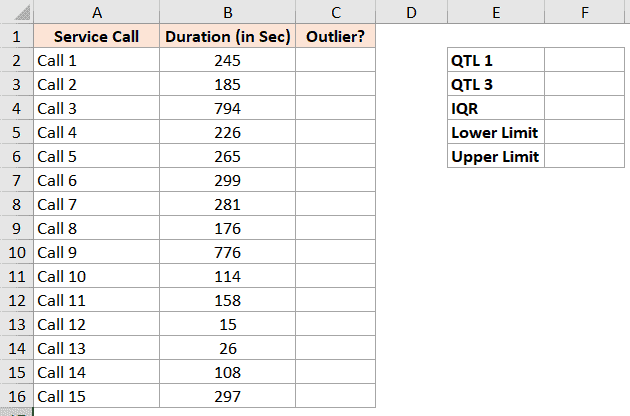
Ниже приведена формула для вычисления первого квартиля в ячейке E2:

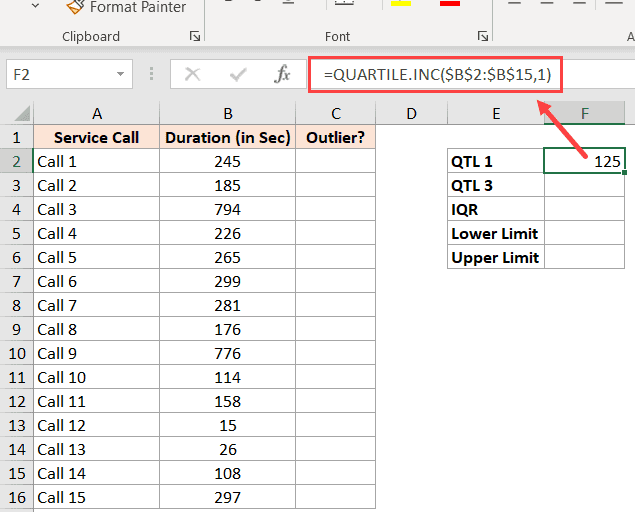
и вот тот, который вычисляет третий квартиль в ячейке E3:

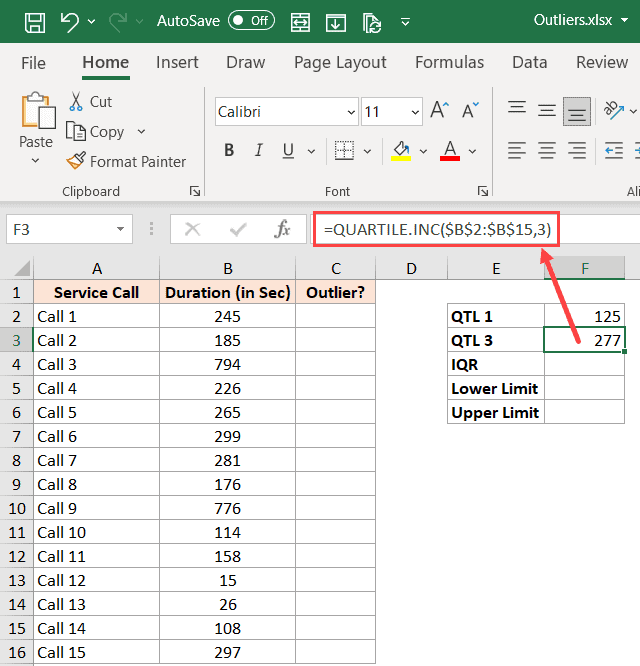
Теперь я могу использовать два вышеупомянутых вычисления, чтобы получить межквартильный размах (который составляет 50% наших данных в пределах 1-го и 3-го квартилей).

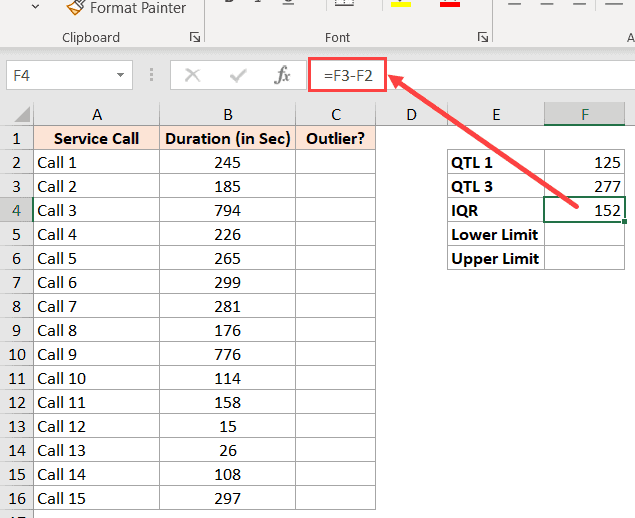
Теперь мы будем использовать межквартильный диапазон, чтобы найти нижний и верхний предел, который будет содержать большую часть наших данных.

Все, что выходит за эти нижние и верхние пределы, будет считаться выбросом.

Ниже приведена формула для расчета нижнего предела: который в нашем примере становится:

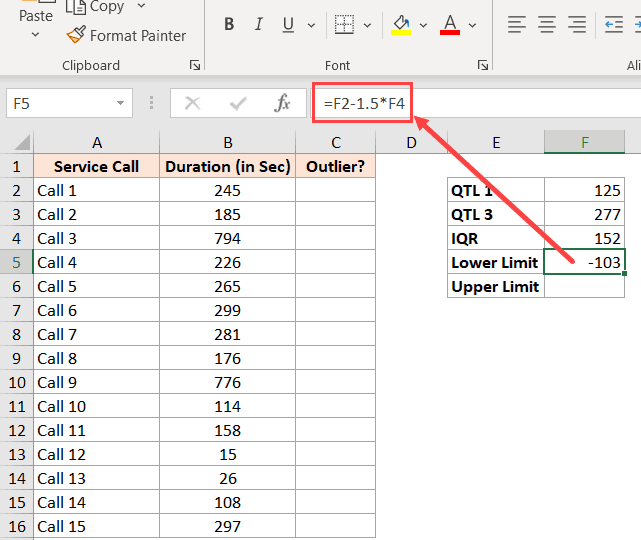
И формула для расчета верхнего предела: который в нашем примере становится:

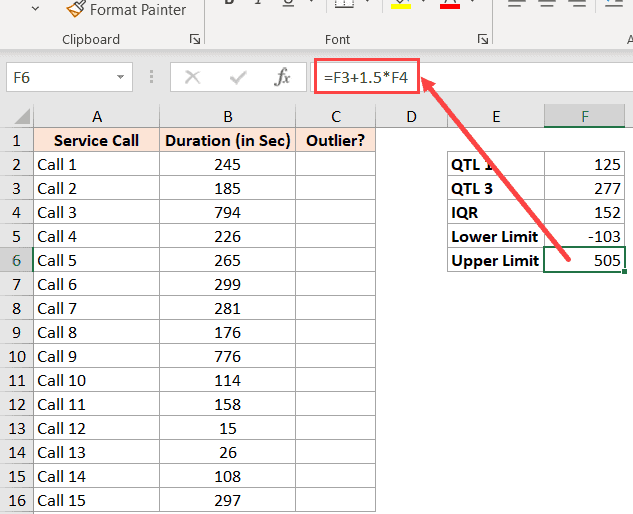
Теперь, когда у нас есть верхний и нижний предел в нашем наборе данных, мы можем вернуться к исходным данным и быстро определить те значения, которые не лежат в этом диапазоне.

Быстрый способ сделать это — проверить каждое значение и вернуть ИСТИНА или ЛОЖЬ в новом столбце.

Я использовал приведенную ниже формулу ИЛИ, чтобы получить ИСТИНА для тех значений, которые являются выбросами.

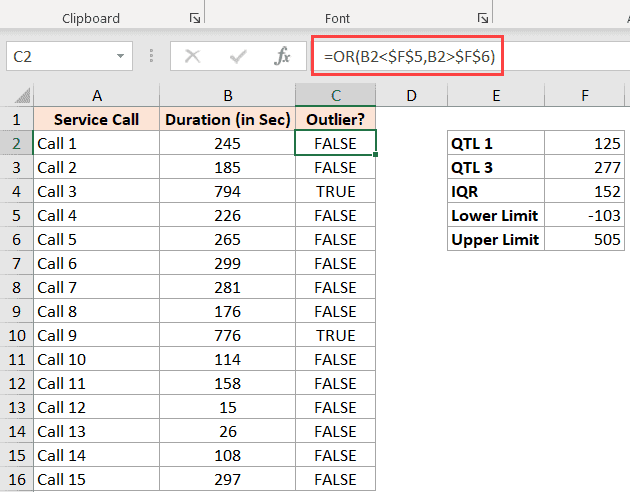
Теперь вы можете фильтровать столбец Outlier и отображать только те записи, для которых значение TRUE.

Кроме того, вы также можете использовать условное форматирование, чтобы выделить все ячейки, в которых значение TRUE.

Расчет средневзвешенного значения в Excel

Допустим, вам нужно найти среднее количество дней для выполнения задач разными сотрудниками. Кроме того, вы хотите вычислить среднюю температуру на определенный день в течение 10-годичного периода времени. Вычисление среднего значения для группы чисел можно выполнить несколькими способами.

Как сделать среднее значение в excel график?

Чаще всего используются обычный линейный тренд и линия скользящего среднего. Линейный тренд – это прямая линия, расположенная таким образом, чтобы расстояние от неё до любой из точек графика было минимальным. Эта линия полезна в том случае, если есть уверенность, что последующие данные будут соответствовать тому же шаблону.

Линии тренда в Excel – это отличный способ получить больше информации об имеющемся наборе данных и о том, как они изменяются со временем. Линейный тренд и скользящее среднее – два типа линий тренда, наиболее распространённых и полезных для бизнеса.

Правила перепечаткиЕще больше уроков по Microsoft Excel

Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами

Ведь в данной задаче могут быть поставлены определенные условия.

Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.

Calculating Moving Averages (SMA, WMA, EMA) using Formulas in Excel

You can also calculate the moving averages using the AVERAGE formula.

In fact, if all you need is the moving average value (and not the standard error or chart), using a formula can be a better (and faster) option than using the Data Analysis Toolpak.

Also, Data analysis Toolpak only gives the Simple Moving Average (SMA), but if you want to calculate WMA or EMA, you need to rely on formulas only.

Calculating Simple Moving Average using Formulas

Suppose you have the dataset as shown below and you want to calculate the 3-point SMA:

In the cell C4, enter the following formula:

=AVERAGE(B2:B4)

Copy this formula for all the cells and it will give you the SMA for each day.

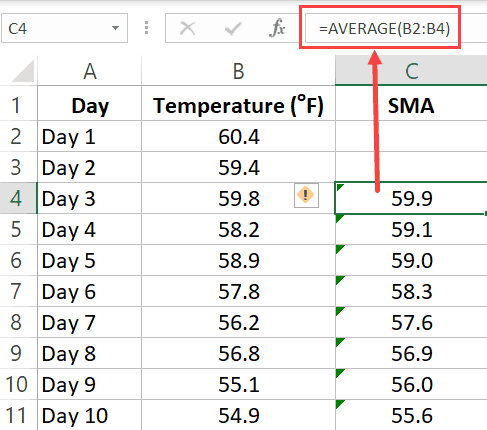
Remember: When calculating SMA using formulas, you need to make sure the references on the formula are relative. This means that the formula can be =AVERAGE(B2:B4) or =AVERAGE($B2:$B4), but it can not be =AVERAGE($B$2:$B$4) or =AVERAGE(B$2:B$4). The row number part of the reference needs to be without the dollar sign. You can read more about absolute and relative references here.

Since we are calculating a 3-point Simple Moving Average (SMA), the first two cells (for the first two days) are empty and we start using the formula from the third day onwards. If you want, you can use the first two values as is, and use the SMA value from the third one onwards.

Calculating Weighted Moving Average using Formulas

For WMA, you need to know the weights that would be assigned to the values.

For example, suppose you need to calculate the 3 point WMA for the below dataset, where 60% weight is given to the latest value, 30% to the one before it and 10% of the one before it.

To do this, enter the following formula in cell C4 and copy for all cells.

=0.6*B4+0.3*B3+0.1*B2

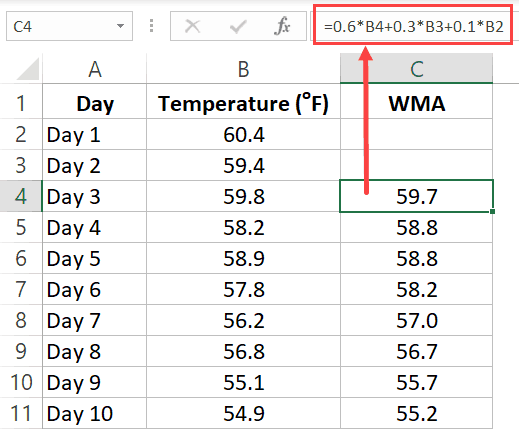
Since we are calculating a 3-point Weighted Moving Average (WMA), the first two cells (for the first two days) are empty and we start using the formula from the third day onwards. If you want, you can use the first two values as is, and use the WMA value from the third one onwards.

Calculating Exponential Moving Average using Formulas

Exponential Moving Average (EMA) gives higher weight to the latest value and the weights keep on getting lower exponentially for earlier values.

Below is the formula to calculate the EMA for a three-point moving average:

EMA =  * (2 / N+1) + Previous EMA

…where N would be 3 in this example (as we are calculating a three-point EMA)

Note: For the first EMA value (when you don’t have any previous value to calculate EMA), simply take the value as is and consider it the EMA value. You can then use this value going forward.

Suppose you have the below data set and you want to calculate the three-period EMA:

In cell C2, enter the same value as in B2. This is because there is no previous value to calculate EMA.

In cell C3, enter the below formula and copy for all cells:

=(B3-C2)*(2/4)+C2

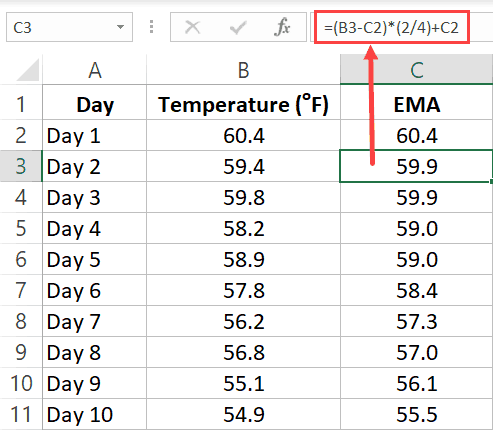
In this example, I have kept it simple and used the latest value and previous EMA value to calculate the current EMA.

Another popular way of doing this is by first calculating the Simple Moving Average and then using it instead of the actual latest value.

Стратегия основанная на направлении движения скользящей средней

1. Определение стороны торговли с помощью скользящей средней. Если она направлена вверх, то вы делаете только покупки, если вниз — то только продажи. При этом точки входа и выхода из рынка определяются на основе других методов скользящих средних (в том числе и на основе более быстрой скользящей).
2. Разворот снизу вверх при положительном наклоне самого ценового рассматривается как сигнал на покупку, разворот сверху вниз при отрицательном наклоне самого ценового рассматривается как сигнал на продажу.
3. Метод скользящего среднего , основанный на пересечение ценой своего скользящего сверху вниз (при отрицательном наклоне обоих) рассматривается как сигнал на продажу, пересечение ценой своего скользящего среднего снизу вверх (при положительном наклоне обоих) рассматривается как сигнал на покупку.
4. Пересечение длинного коротким снизу вверх рассматривается как сигнал к покупке и наоборот.
5. Скользящие средние с круглыми периодами (50, 100, 200) иногда рассматриваются как скользящие уровни и сопротивления.
6. Исходя из того, какие скользящие направлены вверх, а какие вниз определяют какой восходящий а какой нисходящий (краткосрочный, среднесрочный, долгосрочный).
7. Моменты наибольшего расхождения двух средних с разными параметрами понимают как сигнал к возможному изменению тренда.

Именно за счёт этой различной «чувствительности» индикатора к одним и тем же изменениям цены и возникает такое явление как взаимопересечение скользящих средних. Хотя, если быть более точным, то правильнее будет сказать, что быстрая линия пересекает линию медленную. Ну, это всё нюансы, а как же это использовать в торговле?

Вычисление с помощью Мастера функций

Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.

Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.

Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».

Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.

После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.

Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.

Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.

Расчет средневзвешенной цены

Функция вводится полностью вручную. Также можно в ячейку поместить одну при помощи мастера, а после дописать вторую.

Обычно для того, чтобы вычислить усредненное квадратичное отклонение требуется достаточно непростые вычисления. Но в Excel есть готовая формула для получения конечного результата (функция СТАНДОТКЛОН).

Данный показатель привязывается к масштабу исходного значению. Чтобы получить относительный уровень разброса требуется рассчитать коэффициент вариации. Для этого достаточно разделить среднеквадратическое отклонение на усредненное арифметическое

Также стоит учитывать и то, что коэффициент рассчитывается в процентах. Именно поэтому стоит установить формат процентный, а не просто числовой для отображения данных в ячейках.

Надстройка Пакет анализа

Получить Экспоненциально сглаженный ряд можно с помощью надстройки Пакет анализа (Analysis ToolPak). Надстройка доступна из вкладки Данные, группа Анализ.

СОВЕТ: Подробнее о других инструментах надстройки Пакет анализа и ее подключении – читайте в статье.

Разместим исходный числовой ряд в диапазоне B7:B32.

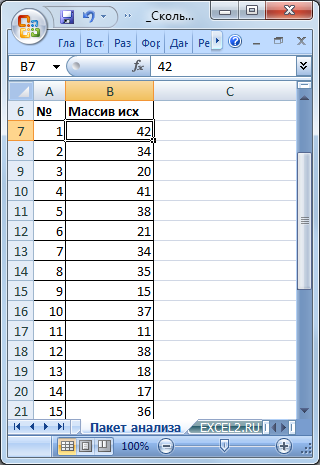
Для наглядности пронумеруем каждое значение ряда (столбец А). Вызовем надстройку Пакет анализа, выберем инструмент Экспоненциальное сглаживание.

В появившемся диалоговом окне в поле Входной интервал введите ссылку на диапазон с данными ряда, т.е. на B7:B32.

Если диапазон включает и заголовок, то нужно установить галочку в поле Метки. В нашем случае устанавливать галочку не требуется, т.к. заголовок столбца не входит в диапазон B7:B32.

Поле Фактор затухания, как и параметр альфа в вышеуказанной формуле, определяет степень сглаживания ряда. Фактор затухания равен (1- альфа). Чем больше Фактор затухания тем глаже получается ряд. Установим значение 0,8.

В поле Выходной интервал достаточно ввести ссылку на левую верхнюю ячейку диапазона с результатами (укажем ячейку D7).

Также поставим галочки в поле Вывод графика и Стандартные погрешности (будет выведен столбец с расчетами погрешностей, англ. Standard Errors). Нажмем ОК.

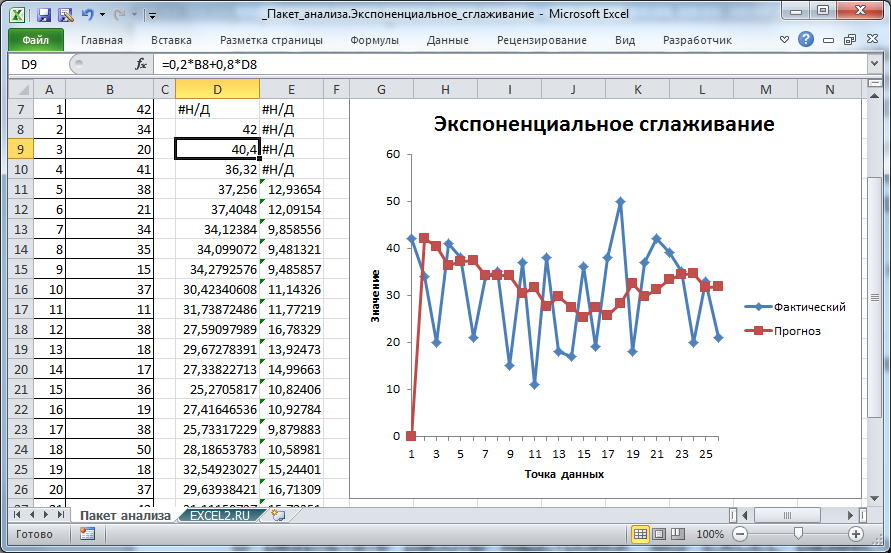
В результате работы надстройки, MS EXCEL разместил значения ряда, полученного методом Экспоненциального сглаживания, в столбце D (см. файл примера лист Пакет анализа ).

В ячейке D7 содержится текстовое значение ошибки #Н/Д, т.к. для получения первого значения Экспоненциального сглаживания требуется значение исходного ряда за предыдущий период.

Первое значение сглаженного ряда, точнее формула = B7 , содержится в ячейке D8. Второе значение вычисляется с помощью формулы = 0,2*B8+0,8*D8 .

Таким образом, Фактор затухания (0,8) определяет вес (вклад) предыдущего значения сглаженного ряда. Соответственно, (1-Фактор затухания)=альфа определяет вес предыдущего значения исходного ряда.