Подбор значения
Лучше попытаться подобрать величину себестоимости с максимальной степенью точности. То есть так, чтобы полная себестоимость произведенной продукции совпала с суммарными затратами завода. Этот вариант тоже можно считать методом назначенной стоимости, но здесь исключается ошибка итоговых расчетов. Очевидно, что перебирать значения вручную достаточно сложно. На практике можно воспользоваться интерфейсным средством Excel «Подбор параметра»:
Решение задачи найдено
Но обратите внимание, что «Подбор параметра» ссылался на контрольную ячейку математической модели, перебирая числа, до тех пор, пока там не оказалось нулевое значение. На практике у вас может не быть подобной контрольной точки, так как ее вычисление связано с множеством внешних данных
Еще один недостаток данного метода – его можно использовать для обработки только одной ячейки (подбора одного числа). Но забывать об этом варианте тоже не стоит – в некоторых случаях он даже удобнее рассматриваемого ниже варианта итерационных расчетов.
Определение срока закрытия кредита
Для многих людей, пользующихся кредитами, важно знать, когда они смогут полностью погасить свой долг. Это позволяет оценить и планировать свои финансовые возможности
В Excel существуют специальные функции, позволяющие определить срок закрытия кредита на основе известных данных.
Для начала необходимо ввести информацию о кредите в таблицу Excel. В отдельных ячейках следует указать сумму кредита, процентную ставку, начальную дату и ежемесячную плату. Затем можно использовать функцию «PMT» для определения суммы платежа по кредиту каждый месяц.
Далее следует найти решение данной задачи путем определения срока погашения кредита. Для этого можно использовать функцию «NPER». В качестве аргументов функция «NPER» принимает процентную ставку, сумму платежа и общий размер кредита.
Пример использования функции «NPER» в Excel:
- В ячейке A1 указывается процентная ставка по кредиту (например, 10%)
- В ячейке A2 указывается ежемесячная плата по кредиту (например, 5000 руб.)
- В ячейке A3 указывается общая сумма кредита (например, 200 000 руб.)
- В ячейке A4 используется функция «NPER» для определения срока погашения кредита: =NPER(A1/12;A2;A3)
В результате, в ячейке A4 будет отображено количество месяцев, необходимых для погашения кредита в заданных условиях. Таким образом, можно быстро и эффективно определить срок закрытия кредита, используя специальные финансовые функции Excel.
Формулы простых и сложных процентов
Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:
- К — начальная сумма вклада;
- К — конечная сумма вклада;
- R — ставка доходности, переводится из процентов в число (10% = 0.1);
- N — количество периодов (лет).
Формула простого процента
По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:
Формула сложного процента
По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:
На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:
где D — сумма регулярных пополнений банковского депозита
Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N)
Ну что, удачи на экзаменах всем читающим меня студентам 
Для закрепления далее мы разберем несколько примеров задач на сложные проценты.
️ ️
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» – 250 рублей. «3» – 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Общие принципы использования финансовых функций в Excel
Microsoft Excel предлагает широкий набор финансовых функций, которые облегчают работу с финансовыми данными и позволяют анализировать и прогнозировать финансовые результаты. В этом разделе мы рассмотрим основные принципы использования финансовых функций в Excel.
1. Синтаксис функций
Каждая финансовая функция в Excel имеет свой уникальный синтаксис. Он состоит из имени функции, открывающей и закрывающей круглых скобок, а также аргументов, разделенных запятыми. Значения аргументов могут быть числами, ссылками на ячейки или другими функциями.
2. Типы аргументов
Финансовые функции могут принимать различные типы аргументов, такие как числа, даты, процентные ставки и другие
Важно правильно указывать типы аргументов при использовании функций для получения точных результатов
3. Работа с диапазонами
В Excel можно использовать финансовые функции не только для отдельных ячеек, но и для целых диапазонов ячеек. Это удобно при работе с большими объемами данных, такими как таблицы с доходами и расходами или прогнозы финансовых показателей.
4. Абсолютные и относительные ссылки
При использовании финансовых функций в Excel важно правильно указывать ссылки на ячейки. Excel использует абсолютные и относительные ссылки, которые определяют, будет ли ссылка изменяться при копировании функции в другие ячейки
Например, абсолютная ссылка будет оставаться неизменной, а относительная ссылка будет автоматически изменяться при копировании.
5. Форматирование результатов
Результаты финансовых функций в Excel могут быть представлены в различных форматах, таких как числа, проценты, даты и другие
Важно выбирать подходящий формат для более наглядного отображения результатов
6. Основные финансовые функции
Excel предлагает множество финансовых функций, которые позволяют выполнять такие операции, как расчет суммы платежей по кредиту, поиск ставки доходности, прогнозирование будущих значений и другие
Важно знать основные функции и правильно выбирать их для решения конкретных задач
7. Настройка параметров функций
Некоторые финансовые функции в Excel имеют дополнительные параметры, которые позволяют настраивать поведение функции. Это может быть, например, указание типа платежей или периода расчета. Знание этих параметров позволяет получить более точные результаты.
8. Использование встроенных функций
Excel предлагает множество встроенных функций, которые могут быть использованы вместе с финансовыми функциями для улучшения и расширения функциональности. Это могут быть функции для работы с датами, текстом, математическими операциями и другими.
Соблюдение этих принципов поможет вам более эффективно использовать финансовые функции в Excel и решать разнообразные задачи связанные с обработкой и анализом финансовых данных.
Задача №1. Работа с финансовыми функциями
В пакете EXCEL встроены специальные
функции для проведения различных финансово-экономических расчетов.
Осуществляется выбор функции с помощью кнопки «Вставка функции» на
панели инструментов, категория — «Финансовые».
Определение будущей стоимости
Будущая стоимость текущего значения вклада при постоянной
процентной ставке рассчитывается с помощью функции:
Б3 (норма; число_периодов; выплата; нз; тип),
где:
норма — процентная ставка за один период;
число _периодов — общее число периодов выплат;
выплата — это выплата, производимая в каждый период,
это значение не может меняться в течение всего периода выплат, обычно выплата
состоит из основного платежа и платежа по процентам, но не включает других
налогов и сборов;
нз — текущая стоимость вклада (настоящее значение),
если аргумент нз опущен, то он полагается равным 0;
тип — это число 0 или 1, обозначающее, когда производится
выплата (1 — в начале периода, 0-в конце периода). Если аргумент тип опущен,
то он полагается равным 0. Параметр тип нужно указывать только
тогда, когда выплата не равна 0, т.е. делаются взносы по периодам.
Задание 1.1. На сберегательный счет в конце каждого месяца
вносятся обязательные платежи по 100 тыс. грн. Рассчитайте, какая сумма
окажется на счете через восемь лет при ставке процента 9.5% годовых.
Решение:
Для расчета применяется формула БЗ, т.к требуется найти
будущее значение выплаченной суммы. В данной задаче при ежемесячном начислении
процентов общее число периодов начисления равно 8*12 (аргумент число_периодов),
а процент за период начисления равен 9,5%/12 (аргумент норма). По
условию аргумент нз = — 100000. Это отрицательна сумма, т.к деньги были
вложены. Выплаты отсутствую, поэтому аргумент выплата отсутствует. Используя
функцию БЗ, получим
Б3 (9,5%/12; 8*12;; — 1000000) = 14297518,58 грн.
Результаты решения задачи представлены в таблице 1.
Динамика роста стоимости показана в рисунке 2.
Таблица 3 содержит расчетные формулы к решению задачи в
пакете Microsoft Excel.
Таблица 1
Расчет будущей стоимости
| A | B | C | D | E | F | G | |
| 1 | ЗАДАНИЕ №1 | ||||||
| 2 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 3 | 1 | 0,007917 | 12 | -100000 | 1 253 653,69р. | ||
| 4 | 2 | 0,007917 | 24 | -100000 | 2 631 729,49р. | ||
| 5 | 3 | 0,007917 | 36 | -100000 | 4 146 575,97р. | ||
| 6 | 4 | 0,007917 | 48 | -100000 | 5 811 767,32р. | ||
| 7 | 5 | 0,007917 | 60 | -100000 | 7 642 224,88р. | ||
| 8 | 6 | 0,007917 | 72 | -100000 | 9 654 350,92р. | ||
| 9 | 7 | 0,007917 | 84 | -100000 | 11 866 175,62р. | ||
| 10 | 8 | 0,007917 | 96 | -100000 | 14 297 518,58р. |
Рисунок 2
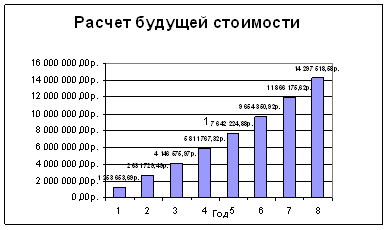
Таблица 3. Расчет будущей стоимости
| A | B | C | D | E | F | G | |
| 1 | ЗАДАНИЕ №1 | ||||||
| 2 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 3 | 1 | =0,095/12 | =12*A3 | -100000 | =БЗ (B3; C3; D3; 0; F3) | ||
| 4 | 2 | =0,095/12 | =12*A4 | -100000 | =БЗ (B4; C4; D4; 0; F4) | ||
| 5 | 3 | =0,095/12 | =12*A5 | -100000 | =БЗ (B5; C5; D5; 0; F5) | ||
| 6 | 4 | =0,095/12 | =12*A6 | -100000 | =БЗ (B6; C6; D6; 0; F6) | ||
| 7 | 5 | =0,095/12 | =12*A7 | -100000 | =БЗ (B7; C7; D7; 0; F7) | ||
| 8 | 6 | =0,095/12 | =12*A8 | -100000 | =БЗ (B8; C8; D8; 0; F8) | ||
| 9 | 7 | =0,095/12 | =12*A9 | -100000 | =БЗ (B9; C9; D9; 0; F9) | ||
| 10 | 8 | =0,095/12 | =12*A10 | -100000 | =БЗ (B10; C10; D10; 0; F10) |
Определение текущей стоимости.
Для расчета текущей стоимости (начальное значение) вклада (займа)
используется функция
П3 (норма; Кпер; выплата; бс; тип),
где:
норма — процентная ставка за один период;
Кпе — общее число периодов выплат;
выплата — это выплата, производимая в каждый периода
бс — будущая стоимость вклада, которую нужно достичь
после последней выплаты, если аргумент бс опущен, то он полагается
равным 0;…
тшп — это число 0 или 1, обозначающее, когда
производится выплата (1 — в начале периода, 0 — в конце периода), если аргумент
пшп опущен, то он полагается равным 0. Параметр mип
нужно указывать, только если выплата не равна 0, т.е. делаются взносы по
периодам.
Задание 1.2 Какую сумму необходимо положить на депозит под
16% годовых, чтобы получить через четыре года 25 млн. грн. при ежеквартальном
начислении процентов?
Решение
Для расчета используем функцию ПЗ.
При этом норма = 16%, Кпер =4, выплата = 2500000 грн., бс =
0.
П3 (16; 4; 2500000;) = — 13 347 704,39р. грн.
Результаты решения задачи представлены в таблице 4. Динамика
роста стоимости показана в рисунке 5. Таблица 6 содержит расчетные формулы к
решению задачи в пакете Microsoft Excel.
Таблица 4
Текущая стоимость
| A | B | C | D | E | F | G | |
| 31 | ЗАДАНИЕ №2 | ||||||
| 32 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 33 | 1 | 16% | 4 | 25000000 | -21370104,78р. | ||
| 34 | 2 | 16% | 8 | 25000000 | -18267255,13р. | ||
| 35 | 3 | 16% | 12 | 25000000 | -15614926,24р. | ||
| 36 | 4 | 16% | 16 | 25000000 | -13347704,39р. |
Рисунок 5
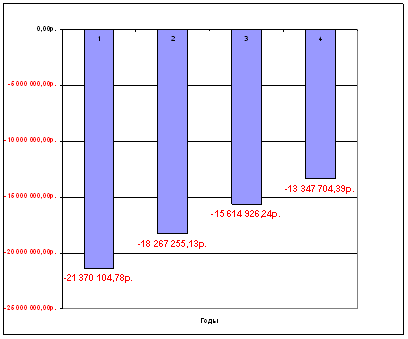
Таблица 6
Текущая стоимость
| A | B | C | D | E | F | G | |
| 28 | ЗАДАНИЕ №2 | ||||||
| 29 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 30 | 1 | 16% | =4*A30 | 25000000 | =ПЗ (B30/4; C30; D30; E30; F30) |
||
| 31 | 2 | 16% | =4*A31 | 25000000 | =ПЗ (B31/4; C31; D31; E31; F31) |
||
| 32 | 3 | 16% | =4*A32 | 25000000 | =ПЗ (B32/4; C32; D32; E32; F32) |
||
| 33 | 4 | 16% | =4*A33 | 25000000 | =ПЗ (B33/4; C33; D33; E33; F33) |
Перекрестный расчет себестоимости
- Подробности
- Создано 10 Март 2013
| crosscosts.xls | 30 kB |
При разработке экономических моделей одной из самых интересных задач является решение проблемы перекрестных связей между формулами. Такие взаимосвязи не позволяют использовать стандартный тип вычислений Excel — прямой алгоритм вычислений дает сообщение о циклической ссылке между формулами. На практике такие задачи встечаются не очень часто. Поэтому вызывают некоторое замешательство даже у опытных пользователей, так как правильно построенный алгоритм не удается реализовать привычным способом в электронных таблицах. Рассмотрим варианты решения подобного рода задачи на примере экономической модели расчета цеховой себестоимости.
Задача № 2. Построение экономической модели вида y=f (x)
Цель экономического регрессионного анализа — на основе
собранных статистических данных, которые представлены в виде таблицы, найти
экономическую модель и произвести на основе этой модели соответствующие
экономические расчеты и прогнозы.
Для построения корреляционного поля необходимо выполнить
следующие действия:
Открыть рабочее окно EXCEL и ввести
значения данных х и у.
Построить точечную диаграмму.
Выполнить пункты меню Диаграмма — Добавить линию тренда.
На вкладке Тип выбрать тип диаграммы, (линейная, логарифмическая, полиноминальная,
степенная, экспоненциальная).
Обратить внимание на то, что в различных вариантах
зависимость может быть любого из перечисленных видов. Далее выбрать вкладку
Параметры и поставить » ٧ » в окне Показать уравнение на
диаграмме
Сделать вывод о виде принятой гипотезы.
Задание. Произвести экономический анализ для заданных
статистических данных. Сделать выбор.
| X | 5,21 | 5,61 | 6,12 | 6,61 | 7,01 | 7,59 | 7,98 | 8,48 | 8,99 | 10,49 |
| Y | 13,4 | 14,12 | 15,34 | 16,52 | 17,02 | 17,78 | 19,06 | 19,96 | 20,78 | 23,98 |
Решение
Выполняем
построение точечной диаграммы и добавляем линию трейда с различными типами
диаграммы:
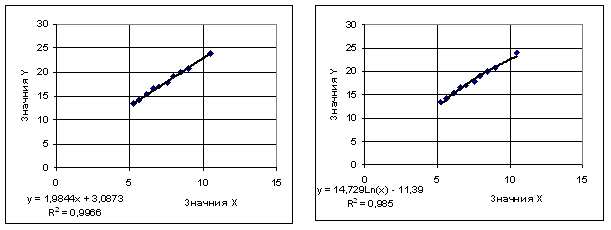— линейная – логарифмическая
— полиноминальная – степенная, экспоненциальная
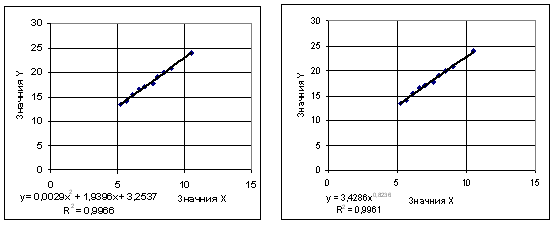
Вывод: проанализировав величину коэффициента достоверности
аппроксимации R2 для каждого типа
зависимости можно сделать вывод, что исходные экономические данные можно
аппроксимировать с наибольшей точностью линейной зависимостью y = 1,9844x +
3,0873 и полиномиальной зависимостью у = 0,0029×2 + +1,9396x + 3,2537, так как
R2 = 0,99966.
Назначенная себестоимость
Для решения задачи можно директивно установить (назначить) величину себестоимости для одного или обоих типов затрат. Например, стоимость электроэнергия устанавливается равной 2 руб за кВт/ч. Этого, в принципе, достаточно для решения нашей проблемы – теплоэнергию уже можно рассчитать по формуле без перекрестных ссылок. Но очевидно возникает другая проблема. Почему назначенная себестоимость равна двум, а не трем рублям? Дополнительно в итоговый расчет себестоимости надо вводить корректирующую сумму, которую непонятно к какому центру затрат отнести. Есть большой риск, что просто будет неверно посчитана полная себестоимость. То есть, себестоимость выработанной продукции не совпадет с затратами всего предприятия.
Как вариант предыдущего метода на практике часто используется в качестве назначенной фактическая себестоимость прошедшего периода (месяца). Этот вариант более устойчив к большим отклонениям в итоговых результатах, но проблему полностью не решает. Скорее это попытка минимизировать риск ошибки, причем в данном варианте обычно опускается расчет корректировок итоговых показателей полной себестоимости.
Пример задачи
На крупном производственном предприятии имеется 2 цеха вспомогательного производства:
- Энергоцех
- Теплоцех
Первый производит электроэнергию для всего предприятия, второй вырабатывает тепло для обогрева всех производственных и административных зданий. Рассматривая каждый цех как центр затрат, можно выделить отдельный бюджет собственных расходов: зарплата персонала, содержание, ремонт, хозяйственные расходы и т.п. Особенностями этих цехов является то, что они формируют составляющие себестоимости продукции, а именно, потребленное электричество и тепло. В нашем случае себестоимость единицы электроэнергии будет равна сумме затрат энергоцеха в рублях, деленной на количество выработанного электричества в натуральном измерении – кВт/ч; аналогично, себестоимость единицы тепла равна сумме затрат теплоцеха в рублях, деленной на общую выработку тепла в натуральном измерении – мДж.
Сложность заключается в том, что сами цеха потребляют энергию друг друга – энергоцех отапливается, а теплоцех потребляет электроэнергию (например, на освещение). В реальной ситуации надо еще учитывать, что какая-то часть собственной энергии каждого цеха идет на внутреннее потребление. Этот момент в задаче не учитывается, так как он принципиально не влияет на алгоритм решения.
Итак, получается, что энергоцех для расчета себестоимости кВт/ч должен учитывать цену потребленного тепла, а теплоцех, в свою очередь, для расчета стоимости мДж должен знать цену кВт/ч. Типичный случай «перекрестной ссылки». Задача, как ни странно, часто встречается на практике именно в такой формулировке. Бывает еще более сложная ситуация, когда вспомогательных цехов с перекрестными затратами несколько: холодильный цех, газо- и водоснабжение, и т.п. Иногда взаимно потребляются полуфабрикаты, произведенные в другом цехе. На большинстве крупных производственных предприятий, особенно с корнями из советского прошлого, до сих пор считают цеховую себестоимость, и приходят в какой-то момент в описанный алгоритмический тупик.
Упрощенная форма задачи представлена в файле примера к статье:
Формула в ячейке В9 (=B8+B7*E10) определяет, что итоговые затраты энергоцеха складываются из бюджета внутренних расходов (в примере представлен одним числом) и стоимостью потребления тепла (объем, умноженный на цену). Ячейка B10 вычисляет себестоимость кВт/ч электроэнергии (=B9/B6). Если попытаться скопировать формулу расчета себестоимости единицы электроэнергии в формулу расчета единицы теплоэнергии (B10 в E10), то логично получим сообщение о циклической ссылке:
Какие же варианты решения имеются и используются на практике?
2.2 Решение поставленных задач.
Для
решение поставленных задач используются
функции ПС(), БС(), ПЛТ(), ПРПЛТ(), ОСПЛТ(),
КПЕР.
Алгоритм
решения задач:
- Внесение
исходных данных; - Ввод функции
с аргументными значениями; - Получение
результата.
Задача
1.
Исходные
данные:
| Сумма кредита |
250000 |
| Срок кредита, лет |
1 |
| Процент | 17% |
Для решения
поставленной задачи использовались функции
ЕСЛИ(), ПС(), ПЛТ(), ПРПЛТ(), ОСПЛТ(), СУММ().
Ежемесячный
платеж рассчитывается с помощью
функции =ПЛТ(Процент/12;Срок
кредита*12;Сумма кредита;;)
Аннуитет,
платежи по кредиту, по процентам и остаток
суммы задолженности рассчитывается по
одинаковой формуле, с изменением № месяца,
для которого производится расчет.
Формула
расчета Аннуитета =ЕСЛИ(№
месяца>Срок кредита*12;0;Ежемесячный
платеж)
Платежи
по кредиту рассчитываются по формуле
=ЕСЛИ(№ месяца>Срок
кредита *12;0;ОСПЛТ(Процент/12;№месяца;Срок
кредита*12;Сумма кредита)).
Процентные
платежи рассчитываются по формуле
ЕСЛИ(№месяца>Срок
кредита*12;0;ПРПЛТ(Процент/12;№месяца;срок
кредита*12;сумма кредита)).
Остаток
суммы задолженности рассчитывается
по формуле =ЕСЛИ(№месяца>Срок
кредита*12;0;ПС(Процент/12;(Срок
кредита *12)-№месяца;
Ежемесячный платеж)).
Общая
сумма процентов рассчитывается
путем суммирований данных из столбца
Проценты.
Мес.
– рассчитывается путем умножения срока
кредита (лет) на 12 месяцев.
Сумма
аннуитета рассчитывается путем умножения
суммы ежемесячного платежа на количество
месяцев.
Результатом
проведения вышеуказанных расчетом
получаем график платежей.
Таблица 2.1 Решение
задачи 1
Планирование в Excel
На основе стратегических целей организации составляются планы и бюджеты. Финансовые задачи на этом этапе — оформление планов и создание финансовой модели организации, в том числе системы бюджетов. Статьи этого раздела:
О финансовой модели организации:
- Что такое финансовая модель и как её создать в Excel (теория)
- Плюсы и минусы использования Excel для создания финансовой модели (теория)
- Правила создания хорошей финансовой модели в Excel (теория)
- Финансовая модель инвестиционного проекта в Excel (практика)
О составлении планов и бюджетировании в Excel:
- Порядок составления бюджета компании (БДР) (теория)
- Простой план продаж в Excel на основе данных прошлых периодов (практика)
- Планирование продаж в Excel с учётом сезонности (практика)
- Простой расчёт точки безубыточности в Excel с построением наглядного графика (практика)
2.1 Постановка задачи:
Необходимо
на практике изучить финансовые функция
для расчетов по кредитам: ПС(), БС(),
ПЛТ(), ПРПЛТ(), ОСПЛТ(), КПЕР.
Для
этого необходимо решить следующие
задачи:
- Рассчитать
аннуитетные платежи по кредиту суммой
250 000 рублей, сроком на 1 год и под 17% годовых.
Составить график платежей, с подробным
описанием платежей непосредственно по
кредиту, по процентам и оставшейся суммой
платежа. (Использование функций ПС(), ПЛТ(),
ПРПЛТ(), ОСПЛТ()). - Рассчитать
сумму ежемесячного вложения под 10% годовых,
которое через 15 лет составит сумму вклада
в 50000 рублей. Выплата производится в начале
периода. (Использование функции ПЛТ()). - Рассчитать
сумму ежемесячного вложения под 10% годовых,
которое через 15 лет составит сумму вклада
50000 рублей, при первоначальном взносе
1000 рублей. (Использование функции ПЛТ()). - Рассчитать
величину вложений под 18 % годовых, которые
будут приносить ежегодно в течение 5 лет
20 000 рублей. (Использование функции ПС()). - Рассчитать
величину первоначальных вложений, под
15% годовых, которое через 10 лет принесет
доход 100000 рублей, при условии внесении
раз в год на счет 2000 рублей. (Использование
функции ПС()). - Вычислить
выплаты по процентам за первый месяц
для трехгодичного займа в 100 000 рублей
из расчета 10% годовых. (Использование
функции ПРПЛТ()). - Вычислить
доход за последний год от трехгодичного
займа в 100000 рублей из расчета 10% годовых
при ежегодных выплатах. (Использование
функции ПРПЛТ()). - Вклад размером
в 5000 рублей положен с 10.01.2010 по 03.04.2010 под
20% годовых. Найти величину капитала на
03.04.2010 при начислении простых процентов.
(Использование функции БС()). - Определить
сумму капитала, если изначально вложена
сумма в размере 10 000 рублей, в банк на
3 года под 15% годовых, далее в течение
всего периода раз в месяц вносится сумма
1000 рублей. Проценты начисляются раз в
месяц, в начале. (Использование функции
БС()). - Определить
будущую стоимость капитала 15000 рублей,
помещенных в банк под 18% годовых, сроком
на 5 лет. Проценты начисляются раз в квартал.
(Использование функции БС()). - Взята сумма
в размере 90000 рублей сроком на 2 года под
15% годовых. Рассчитать сумму остаточных
платежей для каждого года займа. (Использование
функции ОСПЛТ()). - С кредитно-дебетовой
карты взята сумма в размере 70000 рублей
сроком на 3 года под 17% годовых. Рассчитать
сумму остаточных платежей для каждого
квартала займа, при условии, что конец
периода на счету должна быть накоплена
сумма 8000 рублей. (Использование функции
ОСПЛТ()). - Рассчитать
через сколько лет сумма вклада в размере
15 000 рублей достигнет 50000 рублей, при процентной
ставке 15% годовых. (Использование функции
КПЕР()). - Начиная
с 30 лет каждый год на счет в банк вносится
1000 рублей. К какому возрасту человек станет
миллионером, при условии, что процентная
ставка равна 18% годовых. (Использование
функции КПЕР()). - Рассчитать
через сколько лет произойдет полное погашение
займа размером 2500000 рублей, если выплаты
50000 рублей производятся в конце каждого
квартала, а процентная ставка равна 17%
годовых. (Использование функции КПЕР()).
Расчет аннуитетных платежей по кредиту в Excel
За вычисление аннуитета в Excel отвечает функция ПЛТ. Принцип вычисления в общем виде заключается в выполнении следующих шагов:
- Составить исходную таблицу данных.
- Построить график погашения долга для каждого месяца.
- Выделить первую ячейку в столбике «Платежи по кредиту» и ввести формулу расчета «ПЛТ ($В3/12;$В$4;$В$2)».
- Получившееся значение растянуть для всех столбцов таблички.
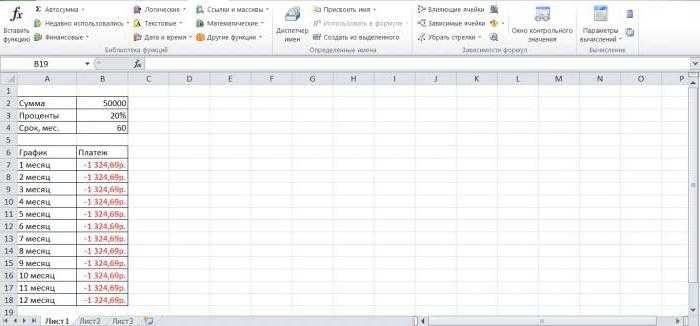Результат работы функции ПЛТ
Расчет в MS Excel погашение основной суммы долга
Аннуитетные платежи должны вноситься ежемесячно определенными суммами. Причем процентная ставка не изменяется.
Вычисление остатка суммы основного долга (при БС=0, тип=0)
Предположим, что кредит на 100000 рублей берется на 10 лет под 9%. Необходимо рассчитать сумму основного долга в 1 месяце 3-го года. Решение:
- Составить таблицу данных и вычислить ежемесячный платеж по приведенной выше формуле ПС.
- Рассчитать долю платежа, необходимую для погашения части долга, по формуле «=-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка)».
- Посчитать сумму основного долга за 120 периодов по известной формуле.
- Используя оператор ПРПЛТ найти количество процентов, выплаченных за 25 месяц.
- Проверить результат.
Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами
Такой расчет лучше сделать простым способом. Нужно использовать следующие формулы для вычисления суммы в промежутке за два периода:
- =«-БС(ставка; кон_период; плт; ; ) /(1+тип *ставка)».
- = «+ БС(ставка; нач_период-1; плт; ; ) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)».
Досрочное погашение с уменьшением срока или выплаты
Если потребуется уменьшить срок кредитования, то придется производить дополнительные вычисления с помощью оператора ЕСЛИ. Так можно будет контролировать нулевой баланс, который не должен быть достигнут раньше окончания сроков выплаты.
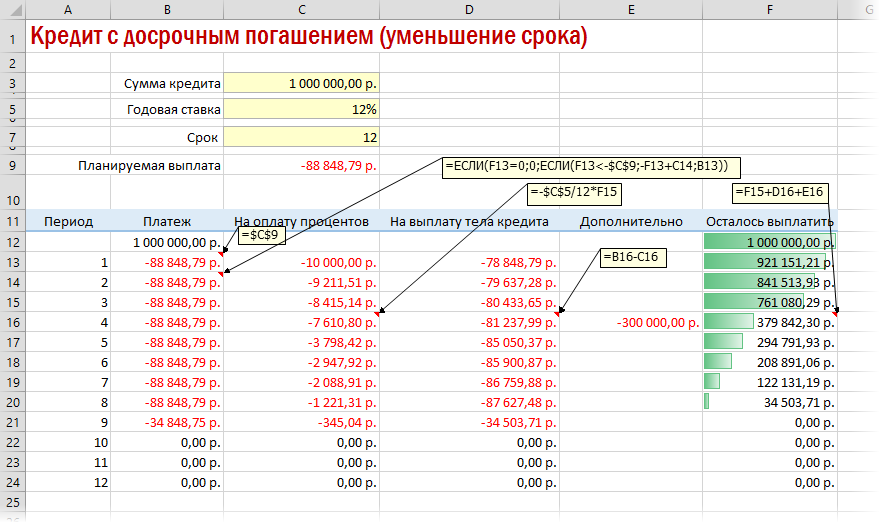Досрочное погашение с уменьшением срока
Чтобы снизить выплаты, нужно пересчитывать взнос за каждый предыдущий месяц.
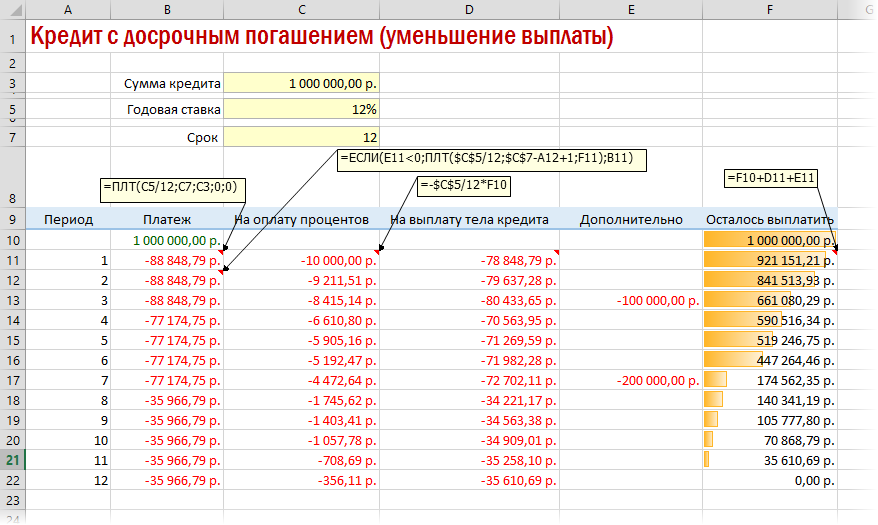Уменьшение выплат кредитования
Кредитный калькулятор с нерегулярными выплатами
Есть несколько вариантов аннуитета, когда заемщик может вносить нефиксированные суммы в любой день месяца. В такой ситуации остаток долга и проценты считаются за каждый день. При этом в Экселе надо:
- Ввести числа месяца, по которым вносятся платежи, и указать их количество.
- Проконтролировать отрицательные и положительные суммы. Отрицательные предпочтительнее.
- Посчитать дни между двумя датами, в которые вносились деньги.
В Excel можно быстро посчитать размер регулярных выплат при условии, что уже накопилась фиксированная сумма. Данное действие выполняется с использованием функции ПЛТ после составления исходной таблицы.
Основная формула аннуитетного платежа в Excel
Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:
Основные значения формулы расшифровываются так:
- АП – аннуитетный платеж (название сокращено).
- О – размер основного долга заемщика.
- ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
- С – число месяцев, на протяжении которых длится кредитование.
Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.
Примеры использования функции ПЛТ в Excel
Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:
- Составить общую таблицу в Excel по исходным данным.
Таблица, составленная по условию задачи. В действительности можно задействовать другие столбцы для ее размещения
- Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
- В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
- В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
- Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».
Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра
- Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».
Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом
Пример расчета суммы переплаты по кредиту в Excel
В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:
- Составить исходную таблицу данных.
Таблица, составленная по условию задачи
- Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
- В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.
Финальный результат. Практически двукратная переплата
Формула вычисления оптимального ежемесячного платежа по кредиту в Excel
Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:
- Составить табличку по исходным данным.
Таблица, составленная по данным из условия задачи
- В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
- Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.
Окончательный результат расчета
Особенности использования функции ПЛТ в Excel
В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:
Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.
EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Чтобы было проще понимать результат, можно переключить отображение ячейки на проценты. А затем растянуть формулу дальше и сравнивать доходность
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
Преимущества и недостатки аннуитетных платежей
Чтобы лучше разбираться в теме, необходимо изучить ключевые особенности данного типа кредитных платежей. Он имеет следующие преимущества:
- Установление конкретной суммы платежа и даты ее взноса.
- Высокая доступность для заемщиков. Практически любой человек сможет оформить аннуитет, независимо от своего финансового положения.
- Возможность понижения суммы ежемесячного взноса с повышением уровня инфляции.
Без недостатков не обошлось:
- Высокая ставка. Заемщик переплатит большую сумму денег по сравнению с дифференциальным платежом.
- Проблемы, возникающие при желании досрочно погасить долг.
- Отсутствие перерасчетов при досрочных выплатах.