Коэффициент корреляции: использование, формулы и пример расчёта в excel

Real Statistics Functions

The Real Statistics Resource Pack furnishes the following worksheet functions:

RSQ_ADJ(R1, R2) = adjusted coefficient of determination  for the data sets contained in ranges R1 and R2.

CORREL_ADJ (R1, R2) = estimated correlation coefficient ρ_est for the data sets contained in ranges R1 and R2.

RSQ_ADJ(r, n) = adjusted coefficient of determination for a sample of size n with correlation coefficient r.

CORREL_ADJ (r, n) = estimated correlation coefficient r_est for a sample of size n with correlation coefficient r.

The Real Statistics Resource Pack also supports the COVARS and COVARP functions, which are equivalent to COVARIANCE.S and COVARIANCE.P, and may be useful to users of Excel 2007 and Excel 2011.

Надстройка Пакет анализа

В надстройке Пакет анализа для вычисления ковариации и корреляции имеются одноименные инструменты анализа .

После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:

Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).

Объяснение

Ковариационная матрица представляет собой квадратную матрицу для понимания взаимосвязей, представленных между различными переменными в наборе данных. Легко и полезно показать ковариацию между двумя или более переменными.

Ковариация будет иметь как положительные, так и отрицательные значения. Положительное значение указывает, что две переменные будут уменьшаться или увеличиваться в одном направлении. Отрицательное значение указывает, что если одна переменная уменьшается, другая увеличивается, и между ними существует обратная связь. Ковариационная матрица представлена ​​в следующем формате. Трехмерная ковариационная матрица показана как

Чтобы создать квадратную ковариационную матрицу 3 × 3, нам нужны трехмерные данные. Диагональные значения матрицы представляют собой дисперсии переменных X, Y и Z (т. Е. COV (X, X), COV (Y, Y) и COV (Z, Z)). Ковариационная матрица симметрична относительно диагонали. Это означает, что COV (X, Y) = COV (Y, X), COV (X, Z) = COV (Z, X) и COV (Y, Z) = COV (Z, Y). Об этой матрице следует помнить, что она является результатом ковариационной матрицы NXN для данных n-мерного размера.

Примеры ковариационной матрицы в Excel

Ниже приведены некоторые примеры использования ковариационной матрицы в Excel.

Выполнение ковариационного анализа оценок, полученных студентами по разным предметам.

Шаг 1: Следующие данные, включая оценки учащихся по математике, английскому языку и естествознанию, считаются такими, как показано на рисунке.

Шаг 2: Перейдите на вкладку «Данные» на ленте и найдите в правом углу набор инструментов «Анализ данных».

Если пакет инструментов «Анализ данных» недоступен, выполните следующие действия.

Шаг А: Перейдите на вкладку «Файл» и выберите «Параметры».

Откроется следующий экран.

Шаг B: Зайдите в Надстройки. В разделе «Параметры управления» убедитесь, что выбран «Надстройки Excel», и нажмите кнопку «Перейти», как показано на рисунке.

Шаг C: Выберите «Analysis-Tool Pak» и «Analysis-ToolPak VBA», как показано на снимке экрана.

После выполнения этих шагов пакет инструментов «Анализ данных» добавляется на вкладку «Данные».

Шаг 3: Щелкните Анализ данных. Откроется диалоговое окно «Анализ данных». Выберите «Ковариацию», прокрутив вверх, и нажмите «ОК».

Он отображает диалоговое окно «Ковариация».

Шаг 5: Выберите диапазон ввода, включая имена субъектов, отметьте «метки в первой строке» и укажите «диапазон вывода» на существующем листе. И нажмите «ОК».

Верхняя часть диагонали пуста, так как ковариационная матрица Excel симметрична относительно диагонали.

Выполните расчет ковариационной матрицы, чтобы определить отклонения между доходностью различных акций портфеля.

Шаг 1: В этом примере учитываются следующие данные, включая доходность акций.

Шаг 2: Открывает диалоговое окно «Анализ данных» и выбирает «Ковариацию», прокручивая вверх и нажимая «ОК».

Он отображает диалоговое окно «Ковариация».

Шаг 3: Выберите диапазон ввода, включая заголовки, отметьте «метки в первой строке» и укажите «диапазон вывода» на существующем листе. И нажмите «ОК».

Верхняя часть диагонали пуста, поскольку ковариационная матрица симметрична по отношению к диагонали.

Расчет ковариационной матрицы котировок акций корпоративных компаний

Шаг 1: В этом примере рассматриваются следующие данные, включая цены на акции различных компаний.

Шаг 2: Открывает диалоговое окно «Анализ данных», выбирает «Ковариацию», прокручивая вверх, и нажимает «ОК».

Он отображает диалоговое окно «Ковариация».

Шаг 3: Выберите диапазон ввода, включая заголовки, отметьте «метки в первой строке» и укажите «диапазон вывода» на существующем листе и нажмите «ОК».

• Как сделать эффект робота в fl studio

    

• Word расстояние между элементами списка

    

• Как перечертить чертеж в автокаде с картинки

    

• Поиск на youtube из контекстного меню браузера

    

• Как сделать яндекс powerpoint

Значения коэффициента корреляции

Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

В случае положительной корреляции при значении:

• 0-0,3 – корреляционная связь очень слабая;
• 0,3-0,5 – слабая;
• 0,5-0,7 – средней силы;
• 0,7-0,9 – высокая;
• 0,9-1 – очень высокая сила корреляции.

Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.

Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:

• очень сильная – показатели ±0,7 — ±1;
• средняя – показатели ±0,3 — ±0,699;
• очень слабая – показатели 0 — ±0,299.

Handling Missing Data

Example 1: Calculate the correlation coefficient between revenue growth and marketing budget growth based on the seven companies in range A3:C10 of Figure 2.

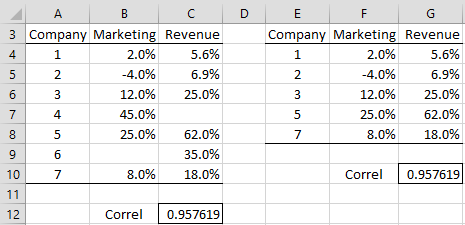
Figure 2 – Correlation coefficient

The correlation coefficient is .9576 (cell C12) as calculated by the formula =CORREL(B4:B10, C4:C10). This indicates that there is a high positive correlation between revenue growth and the growth in the marketing budget.

Note that Excel ignores pairs of data for which one or both of the data elements in the pair are empty or non-numeric. Thus companies 4 and 6 are ignored in the calculation of the correlation coefficient in Example 1; i.e. the formula =CORREL(F4:F8, G4:G8) calculates the same value for the correlation coefficient.

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

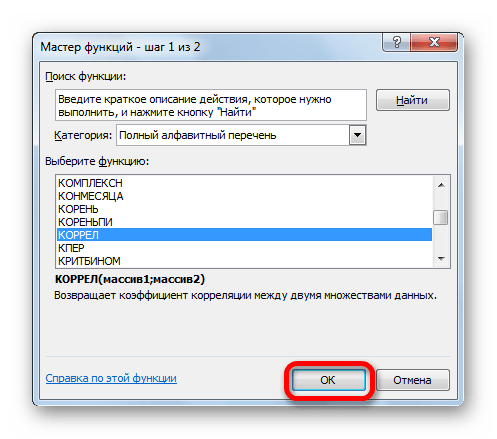
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

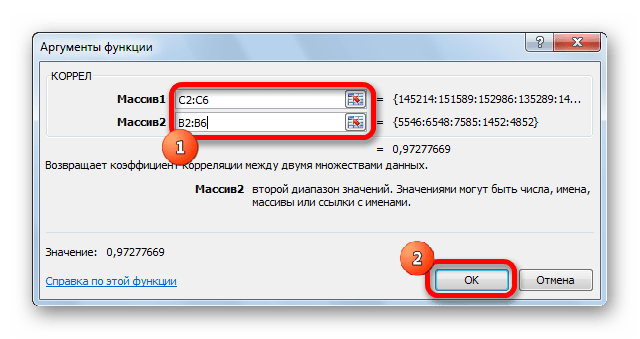
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

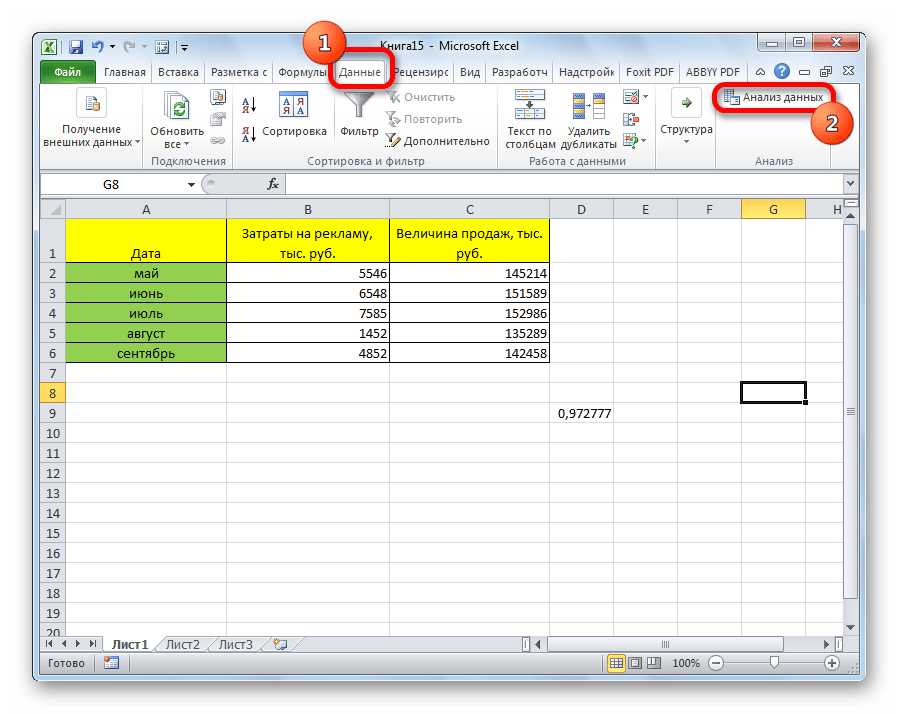
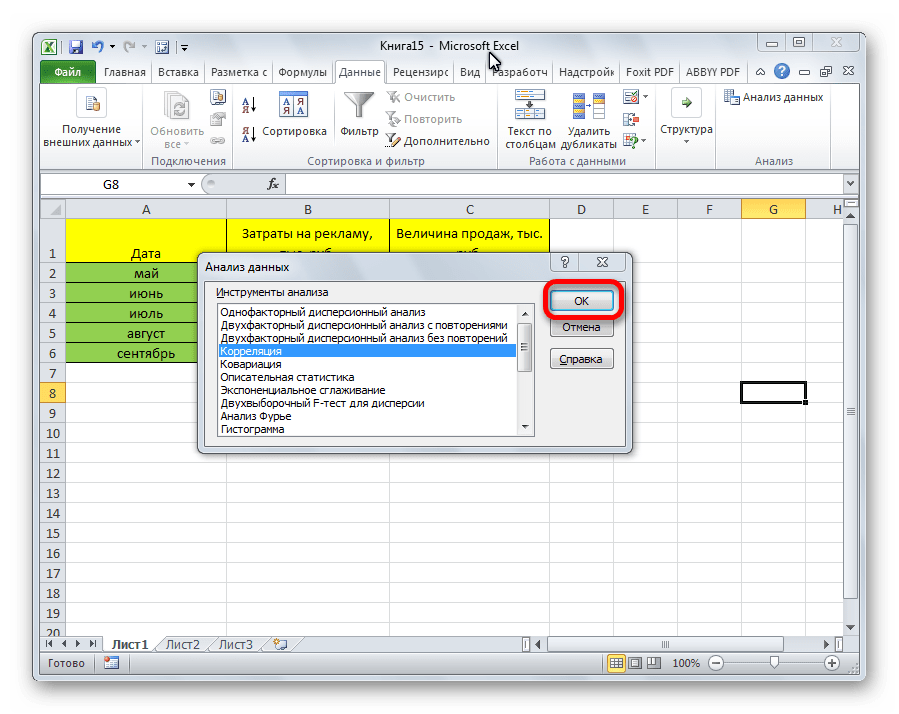
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

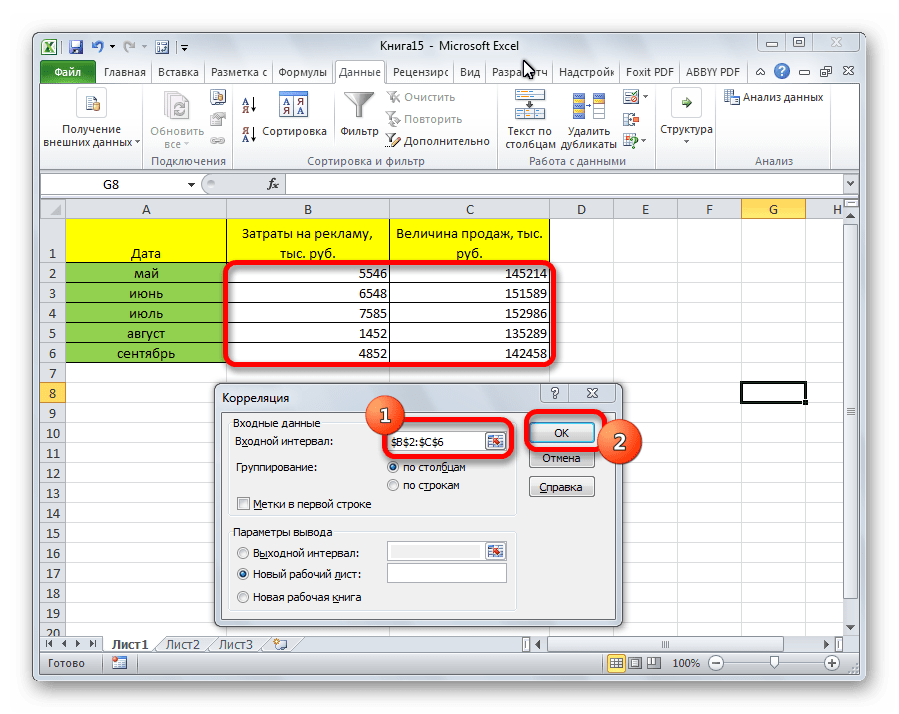
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

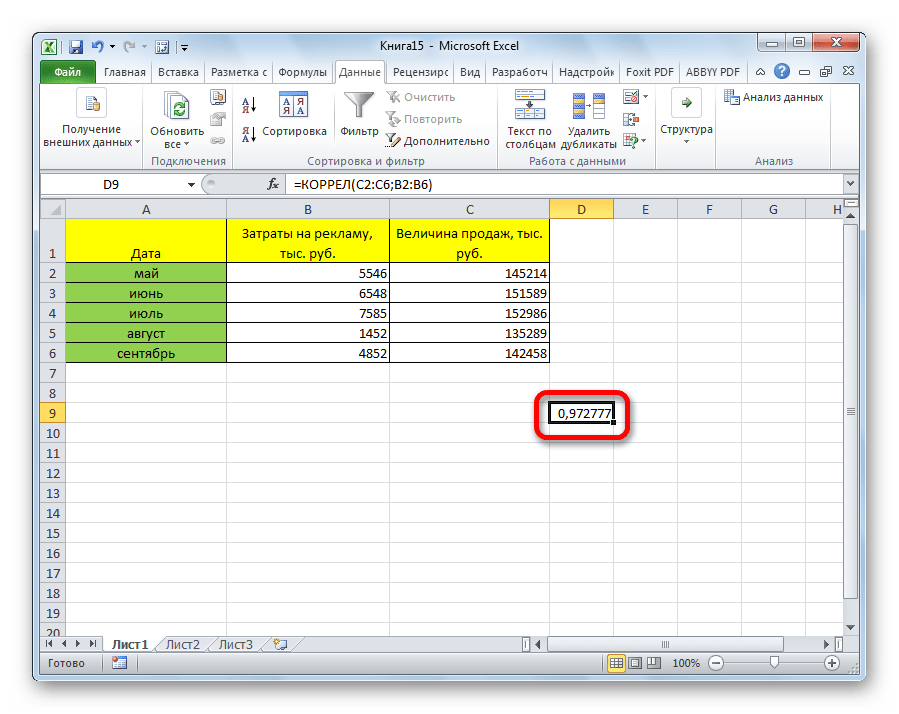
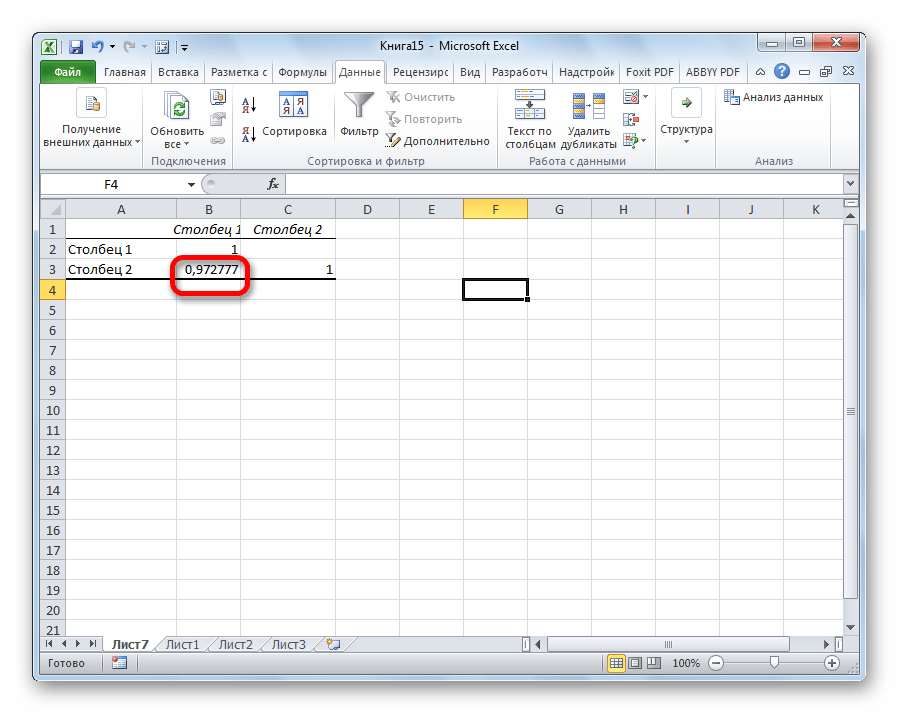
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Линейный коэффициент корреляции Пирсона

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r 2 , который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r 2 = 0,01 или 1%, при r = 0,5 r 2 = 0,25 или 25%.

Использование ковариационной матрицы для анализа данных

Ковариационная матрица представляет собой квадратную матрицу, в которой элементы отражают ковариацию между парами переменных. Если элемент положителен, то это указывает на прямую связь между переменными (то есть, при увеличении значений одной переменной, значения другой переменной также увеличиваются). Если элемент отрицателен, то это указывает на обратную связь (то есть, при увеличении значений одной переменной, значения другой переменной уменьшаются). Если элемент равен нулю, то это указывает на отсутствие связи или независимость между переменными.

Ковариационная матрица может быть использована для ряда анализов данных. Например, она может помочь в анализе рисков и определении взаимосвязей в данных. Она также может быть использована для определения факторов, влияющих на заданные переменные, и для построения моделей прогнозирования.

Для построения ковариационной матрицы в Excel можно воспользоваться функцией COVAR или COVARIANCE.P. Эти функции позволяют вычислить ковариацию между двумя или более переменными в диапазоне данных.

Пример использования функции COVAR:

1. Выберите ячейку, в которой будет находиться значение ковариации.
2. Введите формулу: =COVAR(диапазон1, диапазон2)
3. Нажмите Enter для выполнения формулы.

Полученное значение будет являться ковариацией между двумя выбранными диапазонами данных. Повторите эту процедуру для каждой пары переменных, чтобы построить полную ковариационную матрицу.

Ковариационная матрица может быть визуализирована в виде графика, который показывает силу и направление связей между переменными. Это помогает в понимании структуры данных и их взаимосвязей.

Использование ковариационной матрицы для анализа данных позволяет выявить зависимости и связи между переменными, что помогает в понимании данных и принятии более обоснованных решений.

Особенности использования функций КОВАР, КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel

Функция КОВАР имеет следующий синтаксис:

= КОВАР(массив1;массив2)

Функция КОВАРИАЦИЯ.В имеет следующую синтаксическую запись:

= КОВАРИАЦИЯ.В(массив1;массив2)

Синтаксис функции КОВАРИАЦИЯ.Г:

= КОВАРИАЦИЯ.Г(массив1;массив2)

Все рассматриваемые функции принимают на вход следующие аргументы:

• массив1 – обязательный аргумент, характеризующий первый массив или диапазон ячеек, содержащих данные числового типа, которые являются всей генеральной совокупностью данных (для функций КОВАРИАЦИЯ.Г и КОВАР) или выборкой (для функции КОВАРИАЦИЯ.В);
• массив2 – обязательный аргумент, характеризующий второй массив или диапазон ячеек с числовыми значениями (генеральная совокупность либо выборка, чем обусловлен выбор функции для расчета).

Примечания 1:

1. Все рассматриваемые функции принимают в качестве аргументов массивы или ссылки на диапазоны ячеек, содержащие текстовые, логические, числовые и данные других типов.
2. Число элементов в диапазонах или массивах, переданных в качестве аргументов массив1 и массив2 должны совпадать. В противном случае все рассматриваемые функции вернут код ошибки #Н/Д.
3. При расчете не учитываются значения типа Текст, Имя, логические значения (ИСТИНА, ЛОЖЬ), ссылки на пустые ячейки. Однако ячейки, содержащие числовое значения 0 (нуль), будут учтены.
4. Если рассматриваемые функции в качестве аргументов принимают:

• Диапазоны пустых ячеек, результатом их выполнения будет код ошибки #ЗНАЧ! (принимают по одной пустой ячейке в качестве каждого аргумента) или #ДЕЛ/0! (принимают по несколько пустых ячеек в качестве аргументов);
• Массивы, состоящие из одного элемента или по одной ячейке в качестве каждого аргумента, функции КОВАРИАЦИЯ.Г и КОВАР вернут числовое значение 0, а функция КОВАРИАЦИЯ.В – код ошибки #ДЕЛ/0!.

Примечания 2:

1. Ковариация – величина, характеризующая линейную зависимость, установившуюся между двумя рядами случайных величин X и Y. Она соответствует математическому ожиданию произведения отклонений X и Y от их центров распределений. Коэффициент ковариации может быть выражен отрицательным, положительным числами и нулем, при этом:

• Если с ростом значений X более вероятные появления больших значений Y и наоборот, между двумя диапазонами существует прямая связь, о чем свидетельствует положительное значение коэффициента ковариации;
• Если с ростом X величина Y имеет тенденцию к снижению и наоборот, устанавливается обратная зависимость, выражаемая отрицательным значением коэффициента ковариации;
• Если между X и Y устанавливается слабая взаимосвязь (при изменениях X изменения Y являются непоследовательными, хаотичными), значение коэффициента ковариации стремится к нулю.

Примечания 3:

1. Функция КОВАР являлась стандартной функцией для расчета ковариации в ранних версиях Excel (2007 и более старых) и оставлена для обеспечения совместимости. В последующих версиях Excel она может отсутствовать, поэтому рекомендуется использовать функции КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г.
2. Выборка – это подмножество величин одного множества, называемого генеральной совокупностью. Другими словами, выборкой считается результат ограниченного ряда наблюдений какого-либо одно или нескольких признаков. Например, при изучении банковской системы государства генеральной совокупностью являются все банковские организации страны, а выборкой – банки города Санкт-Петербург.
3. В отличие от коэффициента корреляции, значение коэффициента ковариации не ограничено диапазоном чисел от -1 до 1.
4. При определении коэффициента ковариации одних и тех же двух диапазонов чисел функции КОВАР и КОВАРИАЦИЯ.Г вернут одинаковый результат, отличающийся от числового значения, которое вернет функция КОВАРИАЦИЯ.В, поскольку они используют разные алгоритмы расчетов.

Статистический анализ ковариации показателей в Excel

Пример 3. В таблице Excel введены данные о спросе на алкогольные напитки, индексе цен и уровне дохода населения государства. Проанализировать взаимосвязи между имеющимися данными.

Вид исходной таблицы данных:

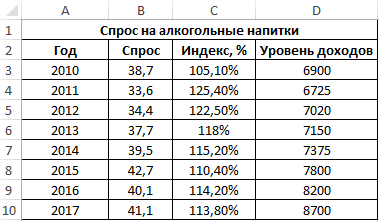
Вначале рассчитаем ковариацию между спросом и индексом цен по формуле:

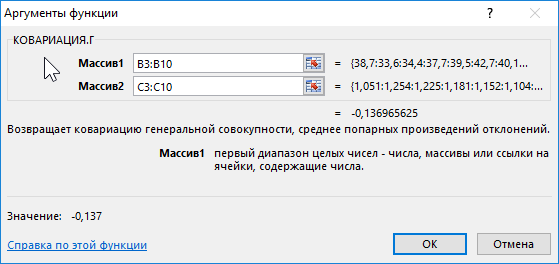
Полученный результат:

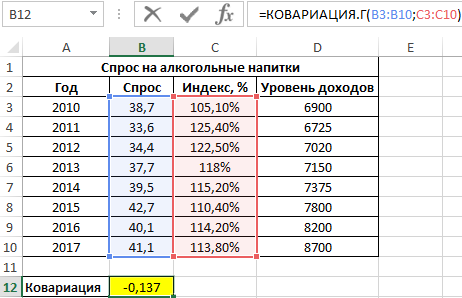
Для оценки степени взаимосвязи двух диапазонов данных удобнее использовать коэффициент корреляции, который можно рассчитать без использования функции КОРРЕЛ следующим способом:

=B12/КОРЕНЬ(ДИСП.Г(B3:B10)*ДИСП.Г(C3:C10))

Функция ДИСП.Г используется для расчета дисперсии генеральной совокупности. Приведенная выше формула наглядно демонстрирует взаимосвязь между коэффициентами ковариации и корреляции.

Полученный результат:

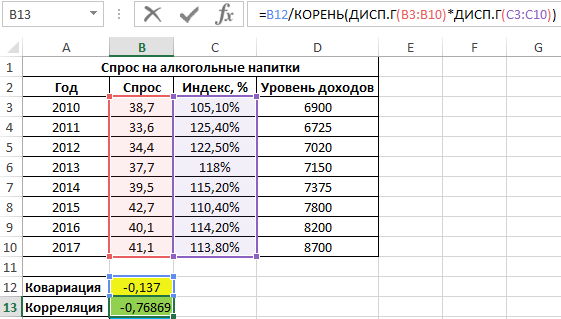
Как видно, между ценами и спросом существует довольно сильная обратная связь. Однако для определения степени влияния спроса определим коэффициент детерминации r2 по формуле:

=СТЕПЕНЬ(B13;2)

Полученное значение, выраженное в процентах:

То есть, примерно 59% вариации спроса за исследуемый период обусловлены изменчивостью цены. Остальные 41% — прочими факторами. А еще одним фактором в данном примере является уровень дохода. Рассчитаем коэффициент корреляции между спросом и доходами с помощью следующей функции:

=КОРРЕЛ(B3:B10;D3:D10)

Результат:

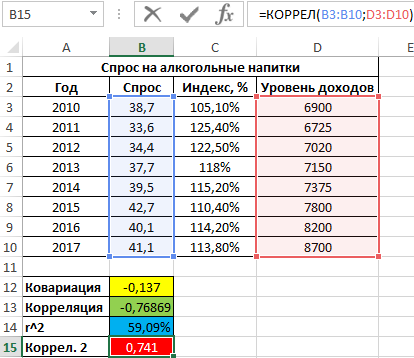
Положительное значение 0,741 соответствует о наличии довольно сильной зависимости между ростом уровня доходов и спросом. Чтобы определить общий коэффициент корреляции и сделать выводы, найдем коэффициент корреляции между индексом цен и уровнем доходов:

=КОРРЕЛ(C3:C10;D3:D10)

Результат:

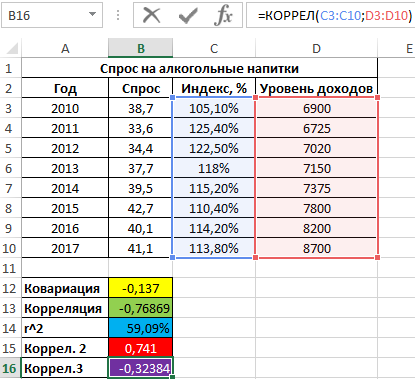
Имеем не сильно выраженную обратную взаимосвязь. Теперь выполним расчет общего коэффициента корреляции по формуле:

=(B13-B15*B16)/КОРЕНЬ((1-СТЕПЕНЬ(B15;2))*(1-СТЕПЕНЬ(B16;2)))

Результат:

Расчеты показывают, что влияние роста цен на уровень спроса «сглаживается» благодаря росту уровня дохода населения. Корень квадратный из последнего значения, взятого по модулю, равен примерно 91%, показывая, насколько вариация цен определяла вариация спроса на алкогольные напитки, если не брать в учет параллельное изменение уровня дохода.

Ковариация против корреляции

Ковариация и корреляция являются двумя понятиями в области вероятности и статистики. Обе концепции описывают отношения между двумя переменными. Кроме того, оба являются инструментами измерения определенного вида зависимости между переменными..

«Ковариация» определяется как «ожидаемое значение вариаций двух случайных отклонений от их ожидаемых значений», а «корреляция» – это «ожидаемое значение двух случайных вариаций».Чтобы упростить, ковариация пытается изучить и измерить, как переменные изменяются вместе. В этой концепции обе переменные могут изменяться одинаково без указания какой-либо связи. Ковариация – это измерение силы или слабости корреляции между двумя или более наборами случайных величин, в то время как корреляция служит масштабированной версией ковариации..

И ковариация и корреляция имеют отличительные типы. Ковариация может быть классифицирована как положительная ковариация (две переменные имеют тенденцию варьироваться вместе) и отрицательная ковариация (одна переменная выше или ниже ожидаемого значения по сравнению с другой переменной). С другой стороны, корреляция имеет три категории: положительная, отрицательная или нулевая. Положительная корреляция обозначается знаком плюс, отрицательная корреляция – знаком минус, а некоррелированные переменные – знаком «0».

И ковариация и корреляция имеют диапазоны. Значения корреляции находятся в масштабе от -1 до +1. С точки зрения ковариации, значения могут превышать или могут быть вне диапазона корреляции. Кроме того, значения корреляции зависят от единиц измерения «X» и «Y».Другое заметное отличие состоит в том, что корреляция безразмерна. Напротив, ковариация описывается в единицах, образованных умножением единицы одной переменной на другую единицу другой переменной. Ковариация фокусируется на отношениях между двумя объектами, такими как переменные или наборы данных. Напротив, корреляция может включать две или более переменных или наборов данных и взаимосвязи между ними.

Другое заметное различие между ними состоит в том, что ковариация часто находится в тандеме с дисперсией (одним из ее свойств, но также и общей мерой рассеяния или дисперсии), тогда как корреляция сочетается с анализом зависимости и регрессии. «Зависимость» определяется как «любая связь между двумя наборами данных или случайными переменными», тогда как регрессионный анализ – это метод, используемый для исследования взаимосвязи между независимыми и зависимыми переменными. Другие классификации корреляции являются частичными и множественными корреляциями.

Резюме:

1. Ковариация и корреляция являются двумя понятиями в изучении статистики и вероятности. Они разные по своим определениям, но тесно связаны. Обе концепции описывают отношения и измеряют вид зависимости между двумя или более переменными.2. Ковариация – это ожидаемая величина отклонения между двумя случайными отклонениями от их ожидаемых значений, в то время как корреляция имеет почти то же определение, но не включает вариацию..3. Ковариация также является мерой двух случайных величин, которые изменяются вместе. Между тем корреляция связана с взаимозависимостью или ассоциацией. Проще говоря, корреляция – это то, насколько далеко или насколько близко две переменные не зависят друг от друга.4. Ковариация – это мера корреляции, а корреляция – это масштабированная версия ковариации..5. Ковариация может включать в себя отношения между двумя переменными или наборами данных, в то время как корреляция может включать в себя также отношения между несколькими переменными..6.Корреляционные значения варьируются от положительного 1 до отрицательного 1. С другой стороны, значения ковариации могут превышать эту шкалу.7. Обе корреляции и ковариации используют положительное или отрицательное описание их типов. Ковариация имеет два типа – положительная ковариация (где две переменные изменяются вместе) и отрицательная ковариация (где одна переменная выше или ниже другой). С точки зрения корреляции, положительные и отрицательные корреляции объединены дополнительной категорией, «0» – некоррелированный тип.