Интервальный прогноз в excel

Пример 1

Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.

Задача. На шести предприятиях проанализировали среднемесячную заработную плату и количество сотрудников, которые уволились по собственному желанию. В табличной форме имеем:

		Количество уволившихся	Зарплата
		30000 рублей
			35000 рублей
			40000 рублей
			45000 рублей
			50000 рублей
			55000 рублей
			60000 рублей

Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а 0 + а 1 x 1 +…+а k x k , где х i — влияющие переменные, a i — коэффициенты регрессии, a k — число факторов.

Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Задание 4. Критерий согласия хи-квадрат.

1. Желательно, чтобы общее количество наблюдений было более 20,
2. Ожидаемая частота, соответствующая нулевой гипотезе должна быть более 5, если ожидаемое явление принимает значение менее 5, то необходимо использовать точный Критерий Фишера.
3. Для четырехпольных таблиц (2х2): Если ожидаемое значение принимает значение менее 10 (а именно 5 <x<10), необходим расчет поправки Йетса таблиц сопряженности
4. Сравниваемые частоты должны быть примерно одного размера
5. Сопоставляемые группы должны быть независимыми (то есть единицы наблюдения в них разные, в отличие от связанных групп, анализирующих изменения «до-после» у одних и тех единиц наблюдений до и после вмешательства. Для таких ситуаций существует отдельный тест МакНемара (McNemar)

Имея созданную таблицу с соответствующими значение, создаем график. Чтобы провести на нём линию тренда надо нажать на график, а именно на область где строится линия. Сверху в панели инструментов выбрать раздел «Макет», а в нём выбрать «Линия тренда». После этого в контексте данного примера в списке выбираем «Экспоненциальное приближение».

Степень нарушения кровообращения	Выписан с хорошим результатом операции	Выписан с удовлетворительным результатом операции	Выписан с ухудшением
II	+7	-4	-3
III	+9	-12	+3
IV	-16	+16
Всего

Задание 4. Критерий согласия хи-квадрат.

Требуется проверить гипотезу о том, что функция распределения выборочных данныхпринадлежит нормальному семейству распределений(экспоненциальному, равномерному семейству).

Пакет Excelпредоставляет возможность вычисления как значений функции надежности, так и значенийp-квантилей хи-квадрат распределения. Эти функции называютсяХИ2РАСПиХИ2ОБР.

Для вычисления нормального распределения можно использовать функцию НОРМРАСП. Подробнее см. ниже в главе “Встроенные функцииExcel”.

Интервалы группировки и частоты попадания в эти интервалы могут быть взяты из задания 2.

Ниже приведен фрагмент листа Excelс примером вычислений, проводимых при построении критерия хи-квадрат для проверки гипотезы нормальности.

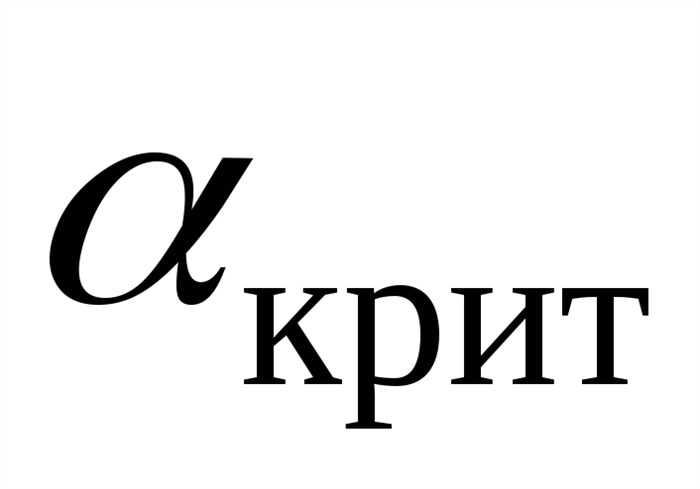
Гипотеза нормальности не может быть принята или отвергнута

Скопировать ячейки A2:B11 с листа “Гисто”, содержащие выборочные частоты, на рабочий лист в ячейкиA3:B12.

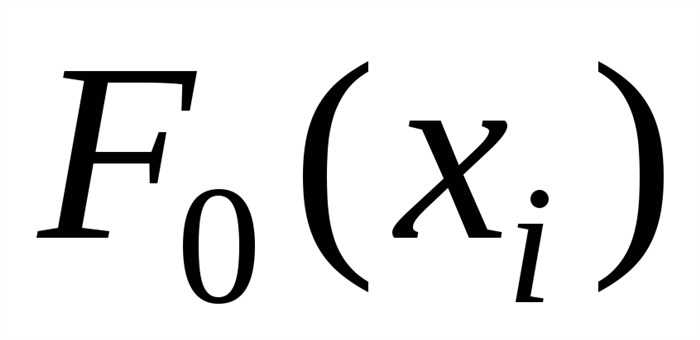
В столбце C (Вероятность) вычислить значение гипотетической функции распределения:

– напомним, что в ячейках B4иB6на листе “Моменты” хранятся среднее и стандартное отклонение;

скопировать ячейку C3во все ячейки столбцаCвплоть до ячейки, соответствующей последней границе (C11);

в ячейке C2указать значение 0(соответствует), а в ячейкеC12– значение1(соответствует).

В столбце D (Ожидаемые частоты) вычислить теоретические частоты:

скопировать ячейку D3в столбцеDдо ячейкиD12(напротив границы “>125,05”);

для контроля в ячейке D13 (Всего)вычисляется сумма значений в столбцеD(должно получиться число101).

В столбце E (Хи-квадрат)вычислить слагаемые статистики:

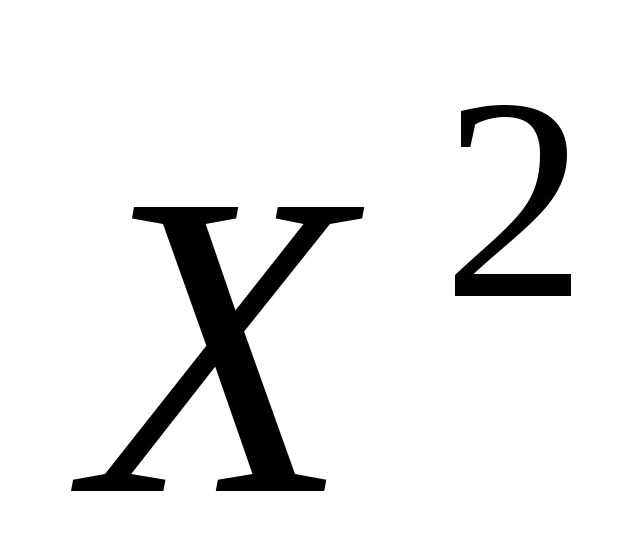
в ячейке E15вычислить сумму значений столбцаE– искомое значение статистики.

“10” – это число групп, для каждого студента оно может быть разным.

Вывод в ячейке F11сделан в соответствии с правилом, описанным в пунктеVIIна стр. 36 пособия .

Замечание 1.При проверке гипотезы экспоненциальности необходимо заменить ячейки, в которых вычисляются значения вероятностей попадания в интервалы (пункт 2) в соответствии с формулой экспоненциального распределения

Критический уровень значимости вычисляется при и пристепенях свободы.

Замечание 2.При проверке гипотезы равномерности необходимо, во-первых, выбрать равномерное разбиение отрезка . Во-вторых, нужно заменить ячейки, в которых вычисляются значения вероятностей попадания в интервалы (пункт 2) в соответствии с формулой равномерного распределения (см. введение)

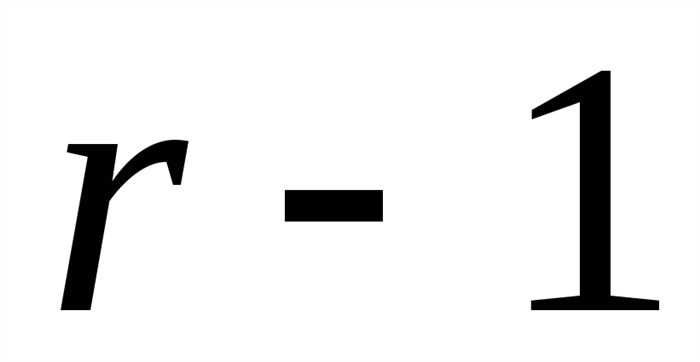
Критический уровень значимости вычисляется при степени свободы.

Выпишите формулу тестовой статистики критерия согласия хи-квадрат. Почему эту статистику можно считать мерой близости выборочных данных к выдвинутой гипотезе?

Какое распределение имеет статистика критерия хи-квадрат?

Почему иногда приходится вычислять два критических уровня значимости?

Чему равен критический уровень значимости при проверке гипотезы о равномерном (нормальном, экспоненциальном) распределении?

Почему при построении критерия хи-квадрат нельзя выбирать интервалы группировки в зависимости от выборочных данных?

Хи-квадрат (χ²): распределение, как его вычислить, примеры — Наука — 2023
Чтобы получить квадратный корень, используйте крышку с (1/2) или 0,5 в качестве экспоненты. Например, чтобы найти квадратный корень из 25, введите в ячейке =25^(1/2) или =25^0,5

Пример расчета и интерпретации коэффициента детерминации в Excel

Шаг 2: Откройте Excel и введите свои данные в два столбца. Например, в столбце А у вас будут значения Х, а в столбце В — значения Y.

Шаг 3: Вычислите среднее значение для каждого массива данных, используя функцию СРЗНАЧЕНИЕ. Например, в ячейке С1 напишите формулу «=СРЗНАЧ(А1：А10)», где 10 — это количество значений в вашем массиве данных, а А1：А10 — это диапазон ячеек с значениями Х. Аналогично вычислите среднее значение для столбца В.

Шаг 4: Вычислите разницу между значениями каждого массива данных и их средним значением. Для этого в ячейке D1 напишите формулу «=А1-С1», где А1 — это значение Х, С1 — это среднее значение Х. Аналогично вычислите разницу между значениями столбца В и их средним значением.

Шаг 5: Вычислите квадрат каждой разности, используя функцию СТЕПЕНЬ. Для этого в ячейке E1 напишите формулу «=СТЕПЕНЬ(D1,2)», где D1 — это разница между значением и средним значением Х. Аналогично вычислите квадрат каждой разности столбца В.

Шаг 6: Вычислите сумму всех квадратов разностей. Для этого напишите формулу «=СУММ(Е1：Е10)», где Е1：Е10 — диапазон ячеек с квадратами разностей. Это общая сумма квадратов отклонений (SSTO).

Шаг 7: Вычислите сумму квадратов отклонений предсказанных значений, используя функцию КВ.СУММ. Для этого напишите формулу «=КВ.СУММ(B1:B10-С1)», где B1:B10 — это столбец В с зависимыми переменными, С1 — это среднее значение Y. Это сумма квадратов отклонений предсказанных значений (SSE).

Шаг 8: Вычислите коэффициент детерминации, используя формулу «=1-SSE/SSTO».

Шаг 9: Интерпретируйте полученный коэффициент детерминации. Если его значение близко к 1, то модель линейной регрессии хорошо объясняет вариацию данных, так как большая часть отклонений может быть объяснена независимой переменной. Если значение близко к 0, то модель слабо объясняет данные, и большая часть отклонений остается неразъясненной.

Статистический анализ ковариации показателей в Excel

Пример 3. В таблице Excel введены данные о спросе на алкогольные напитки, индексе цен и уровне дохода населения государства. Проанализировать взаимосвязи между имеющимися данными.

Вид исходной таблицы данных:

Вначале рассчитаем ковариацию между спросом и индексом цен по формуле:

Для оценки степени взаимосвязи двух диапазонов данных удобнее использовать коэффициент корреляции, который можно рассчитать без использования функции КОРРЕЛ следующим способом:

Функция ДИСП.Г используется для расчета дисперсии генеральной совокупности. Приведенная выше формула наглядно демонстрирует взаимосвязь между коэффициентами ковариации и корреляции.

Как видно, между ценами и спросом существует довольно сильная обратная связь. Однако для определения степени влияния спроса определим коэффициент детерминации r2 по формуле:

Полученное значение, выраженное в процентах:

То есть, примерно 59% вариации спроса за исследуемый период обусловлены изменчивостью цены. Остальные 41% — прочими факторами. А еще одним фактором в данном примере является уровень дохода. Рассчитаем коэффициент корреляции между спросом и доходами с помощью следующей функции:

Положительное значение 0,741 соответствует о наличии довольно сильной зависимости между ростом уровня доходов и спросом. Чтобы определить общий коэффициент корреляции и сделать выводы, найдем коэффициент корреляции между индексом цен и уровнем доходов:

Имеем не сильно выраженную обратную взаимосвязь. Теперь выполним расчет общего коэффициента корреляции по формуле:

Расчеты показывают, что влияние роста цен на уровень спроса «сглаживается» благодаря росту уровня дохода населения. Корень квадратный из последнего значения, взятого по модулю, равен примерно 91%, показывая, насколько вариация цен определяла вариация спроса на алкогольные напитки, если не брать в учет параллельное изменение уровня дохода.

Для определения степени зависимости между несколькими показателями применяется множественные коэффициенты корреляции. Их затем сводят в отдельную таблицу, которая имеет название корреляционной матрицы. Наименованиями строк и столбцов такой матрицы являются названия параметров, зависимость которых друг от друга устанавливается. На пересечении строк и столбцов располагаются соответствующие коэффициенты корреляции. Давайте выясним, как можно провести подобный расчет с помощью инструментов Excel.

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

1. Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
2. Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
3. Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
4. Жмем «Закрыть».

• 0x8004011d outlook 2016 сервер недоступен

    

• По каким причинам 1с может потребовать исключить кд из реестра

    

• Программа настройки процессора md lab

    

• Преобразовывать загруженные файлы в формат google

    

• 1с ошибка runtime error

Как рассчитать коэффициент детерминации в Excel?

Для начала, вам необходимо иметь данные для зависимой переменной и независимых переменных в виде двух столбцов в Excel. Определите ячейки, содержащие значения зависимой и независимых переменных.

Затем введите формулу RSQ в пустую ячейку, например, =RSQ(A2:A10, B2:B10), где A2:A10 — диапазон ячеек для независимых переменных, а B2:B10 — диапазон ячеек для зависимой переменной.

После ввода формулы нажмите Enter, и Excel рассчитает коэффициент детерминации. Значение коэффициента будет отображено в ячейке, где вы ввели формулу.

Коэффициент детерминации в Excel будет иметь значение от 0 до 1, где 0 означает отсутствие связи между переменными, а 1 означает полную связь.

Обратите внимание, что коэффициент детерминации может быть только положительным числом и не отражает направление и силу связи между переменными. Используя функцию RSQ в Excel, вы можете быстро и легко рассчитать коэффициент детерминации для ваших данных и оценить степень связи между переменными

Используя функцию RSQ в Excel, вы можете быстро и легко рассчитать коэффициент детерминации для ваших данных и оценить степень связи между переменными.

Вычисление множественного коэффициента корреляции

Принято следующим образом определять уровень взаимосвязи между различными показателями, в зависимости от коэффициента корреляции:

• 0 – 0,3 – связь отсутствует;
• 0,3 – 0,5 – связь слабая;
• 0,5 – 0,7 – средняя связь;
• 0,7 – 0,9 – высокая;
• 0,9 – 1 – очень сильная.

Если корреляционный коэффициент отрицательный, то это значит, что связь параметров обратная.

Для того, чтобы составить корреляционную матрицу в Экселе, используется один инструмент, входящий в пакет «Анализ данных». Он так и называется – «Корреляция». Давайте узнаем, как с помощью него можно вычислить показатели множественной корреляции.

Этап 1: активация пакета анализа

Сразу нужно сказать, что по умолчанию пакет «Анализ данных» отключен. Поэтому, прежде чем приступить к процедуре непосредственного вычисления коэффициентов корреляции, нужно его активировать. К сожалению, далеко не каждый пользователь знает, как это делать. Поэтому мы остановимся на данном вопросе.

1. Переходим во вкладку «Файл». В левом вертикальном меню окна, которое откроется после этого, щелкаем по пункту «Параметры».

После указанного действия пакет инструментов «Анализ данных» будет активирован.

Этап 2: расчет коэффициента

Теперь можно переходить непосредственно к расчету множественного коэффициента корреляции. Давайте на примере представленной ниже таблицы показателей производительности труда, фондовооруженности и энерговооруженности на различных предприятиях рассчитаем множественный коэффициент корреляции указанных факторов.

1. Перемещаемся во вкладку «Данные». Как видим, на ленте появился новый блок инструментов «Анализ». Клацаем по кнопке «Анализ данных», которая располагается в нём.

Так как у нас факторы разбиты по столбцам, а не по строкам, то в параметре «Группирование» выставляем переключатель в позицию «По столбцам». Впрочем, он там уже и так установлен по умолчанию. Поэтому остается только проверить правильность его расположения.

Около пункта «Метки в первой строке» галочку ставить не обязательно. Поэтому мы пропустим данный параметр, так как он не повлияет на общий характер расчета.

В блоке настроек «Параметр вывода» следует указать, где именно будет располагаться наша корреляционная матрица, в которую выводится результат расчета. Доступны три варианта:

• Новая книга (другой файл);
• Новый лист (при желании в специальном поле можно дать ему наименование);
• Диапазон на текущем листе.

Давайте выберем последний вариант. Переставляем переключатель в положение «Выходной интервал». В этом случае в соответствующем поле нужно указать адрес диапазона матрицы или хотя бы её верхнюю левую ячейку. Устанавливаем курсор в поле и клацаем по ячейке на листе, которую планируем сделать верхним левым элементом диапазона вывода данных.

Этап 3: анализ полученного результата

Теперь давайте разберемся, как понимать тот результат, который мы получили в процессе обработки данных инструментом «Корреляция» в программе Excel.

Как видим из таблицы, коэффициент корреляции фондовооруженности (Столбец 2) и энерговооруженности (Столбец 1) составляет 0,92, что соответствует очень сильной взаимосвязи. Между производительностью труда (Столбец 3) и энерговооруженностью (Столбец 1) данный показатель равен 0,72, что является высокой степенью зависимости. Коэффициент корреляции между производительностью труда (Столбец 3) и фондовооруженностью (Столбец 2) равен 0,88, что тоже соответствует высокой степени зависимости. Таким образом, можно сказать, что зависимость между всеми изучаемыми факторами прослеживается довольно сильная.

Как видим, пакет «Анализ данных» в Экселе представляет собой очень удобный и довольно легкий в обращении инструмент для определения множественного коэффициента корреляции. С его же помощью можно производить расчет и обычной корреляции между двумя факторами.

Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.

Коэффициент детерминации в Excel (Эксель)

Для статистических моделей во многих случаях необходимо определить точность прогноза. Это производится с помощью специальных расчётов в Microsoft Excel, а использоваться будет коэффициент детерминации. Он обозначается как R^2.

Статистические модели можно разделить на качественные уровни в зависимости от коэффициента. От 0.8 до 1 относятся модели хорошего качества, модели достаточного качества имеют уровень от 0.5 до 0.8, а плохое качество имеет диапазон от 0 до 0.5.

Способ определения точности с помощью функции КВПИРСОН

В линейной функции коэффициент детерминации будет равен квадрату корреляционного коэффициента. Рассчитать его можно с помощью специальной функции. Для начала создадим таблицу с данными.

Потом нужно выбрать место, где будет показан результат расчёта и нажимаем на кнопку вставки функции.

После этого откроется специальное окно. Категорию нужно выбрать «Статистические» и выбираем КВПИРСОН. Эта функция позволяет определить коэффициент корреляции касательно функции Пирсона, соответственно квадратное значение коэффициента корреляции = коэффициенту детерминации.

После подтверждения действия, появится окно в котором нужно в полях выставить «Известные значения Х» и «Известные значения Y». Нажимаем мышкой поле «Известные значения Y» и в рабочем окне выделяем данные столбца Y. Аналогичное действие делаем и с другим полем выбирая данные уже с таблицы Х.

Как результат этих действий будет показано значение коэффициента детерминации в ячейке, которая ранее была выбрана для отображения результата.

Определение коэффициента детерминации если функция не является линейной.

Если функция нелинейная, то инструментарий Excel также позволяет рассчитать коэффициент с помощью инструмента «Регрессия». Его можно найти в пакете анализа данных. Но для начала нужно активировать этот пакет, перейдя в раздел «Файл» и в списке открыть «Параметры».

После этого можно увидеть новое окно, в котором нужно в меню выбрать «Надстройки», а в специальном поле по управлению надстройками выбираем «Надстройки Excel» и переходим к ним.

После перехода в надстройки Excel появится новое окно. В нём можно увидеть доступные для пользователя надстройки. Ставим галочку возле «Пакет анализа» и подтверждаем действие.

Найти его можно в разделе «Данные», после перехода в который нажимаем на «Анализ данных» в правой части экрана.

После его открытия, в списке выбираем «Регрессия»и подтверждаем действие.

В рабочем окне появится результат. Так как мы вычисляем коэффициент детерминации, то в итогах нам нужен R-коэффициент. Если посмотреть на значение, то можно увидеть что оно относится к наилучшему качеству.

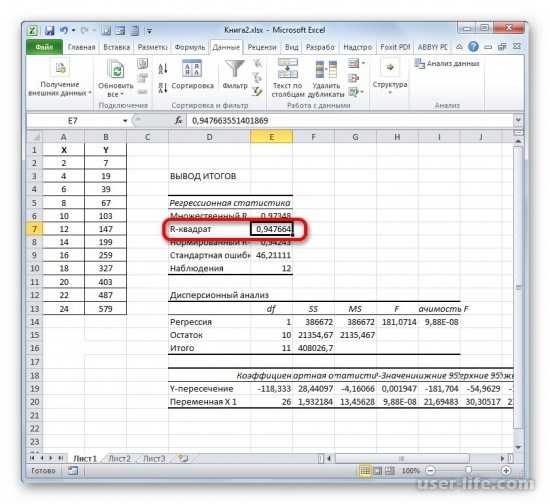
Способ определения коэффициента детерминации для линии тренда

Имея созданную таблицу с соответствующими значение, создаем график. Чтобы провести на нём линию тренда надо нажать на график, а именно на область где строится линия. Сверху в панели инструментов выбрать раздел «Макет», а в нём выбрать «Линия тренда». После этого в контексте данного примера в списке выбираем «Экспоненциальное приближение».

Линия тренда будет отображена на графике как кривая с черным цветом.

Для того чтобы показать коэффициент детерминации, нужно по черной кривой нажать правой кнопкой мыши и выбрать в списке «Формат линии тренда».

После этого появится новое окно. В нём нужно отметить флажком и выбрать нужное действие (показано на скриншоте). Благодаря этому коэффициент будет отображен на графике. После того как это было сделано, закрываем окно.

После закрытия окна формата линии тренда в рабочем окне можно увидеть значение коэффициента детерминации.

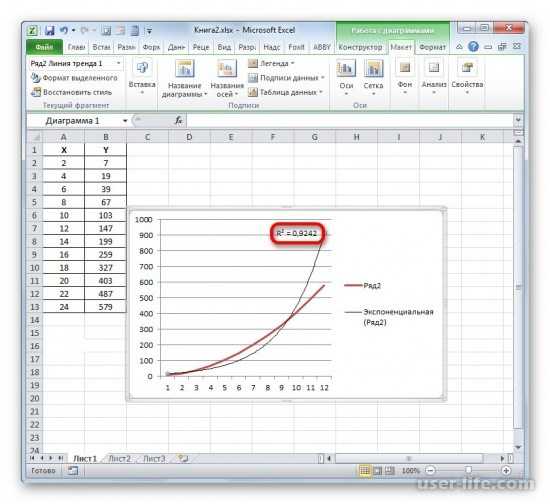
Если пользователю нужен другой типаж линии тренда, то в окне «Формат линии тренда» можно выбрать его. Не забыв задать его ранее при создании линии тренда в разделе «Макет» или в контекстном меню. Также не забываем ставить флажок для функции R^2.

Как результат можно увидеть изменение линии тренда и число достоверности.

После просмотра разных вариаций линий тренда, пользователь может определить наиболее подходящую для себя так как показатель достоверности может меняться в зависимости от выбора линии. Максимальный коэффициент это единица, что означает максимальную достоверность, однако не всегда можно достигнуть этого значения.

Так было рассмотрено несколько способов по нахождению коэффициента детерминации. Пользователь может выбрать наиболее оптимальный для своих целей.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

• линейной (у = а + bx);
• параболической (y = a + bx + cx 2 );
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

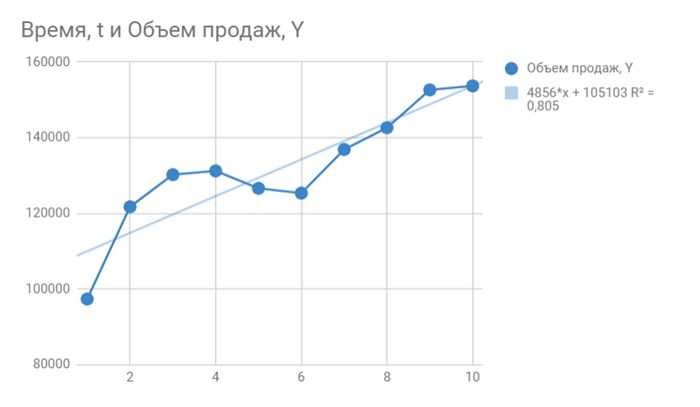
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации

В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Разбор результатов анализа

Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат
. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.

Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение»
и столбца «Коэффициенты»
. Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.

Значение на пересечении граф «Переменная X1»
и «Коэффициенты»
показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.

Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.

Разбор результатов анализа

Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.

Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.

Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.

Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:

ŷ — ожидаемое значение у при заданном значении х,

x — независимая переменная,

a — отрезок на оси y для прямой линии,

b — наклон прямой линии.

На рисунке ниже это понятие представлено графически:

На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.

Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением

На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4

Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следу­ющего уравнения:

ŷ = 2 + 0.5х =2 +0.5(2) =3.

Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.

Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по методу наименьших квадратов.

Изучение результатов и выводы

«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:

СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.

В более привычном математическом виде его можно записать, как:

y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844

Данные для АО «MMM» представлены в таблице:

Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.

Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.

Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.