Транспортная задача в microsoft excel

Транспортная задача: описание

Используя транспортную задачу, можно найти оптимальный вариант перевозки с минимальными затратами между двумя взаимодействующими контрагентами (в данной статье мы будем рассматривать покупателей и продавцов). Для начала решения необходимо представить исходные данные в схематическом или матричном виде. Последний вариант используется в Excel.

Транспортные задачи бывают двух типов:

• Закрытый — общее предложение продавца равно общему спросу.
• открытый — спрос и предложение не равны. Чтобы решить такую ​​задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с отсутствующим количеством спроса или предложения. Также в таблице себестоимости должна быть сделана соответствующая запись (с нулевыми значениями).

Пример решения транспортной задачи в Excel

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
2. Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
3. Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
4. Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
5. Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
6. Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
7. Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
8. Копируем маркером заполнения формулу на всю строку.
9. Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
10. Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
11. Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
12. Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
13. После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Мы рады, что смогли помочь Вам в решении проблемы.

Решение транспортной задачи в Excel с примером и описанием

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

• в виде схемы;
• в виде матрицы.

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

• открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
• закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.

Пример решения транспортной задачи в Excel

Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители	Потребители	Объем производства
В1	В2	В3	В4	В5
А1	4,2	4	3,35	5	4,65	246
А2	4	3,85	3,5	4,9	4,55	186
А3	4,75	3,5	3,4	4,5	4,4	196
А4	5	3	3,1	5,1	4,4	197
Объем потребления	136	171	71	261	186

Задача: минимизировать транспортные расходы по перевозке продукции.

1. Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
2. Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
3. Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
4. Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
5. Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
6. Вносим известные значения потребности в товаре и объема производства.
7. Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
8. Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
9. Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

• суммарный объем производства превышает суммарную потребность в товаре;
• суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.

Пример решения транспортной задачи в Excel

Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители	Потребители	Объем производства
	В1	В2	В3	В4	В5
А1	4,2	4	3,35	5	4,65	246
А2	4	3,85	3,5	4,9	4,55	186
А3	4,75	3,5	3,4	4,5	4,4	196
А4	5	3	3,1	5,1	4,4	197
Объем потребления	136	171	71	261	186

Задача: минимизировать транспортные расходы по перевозке продукции.

1. Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
2. Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
3. Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.

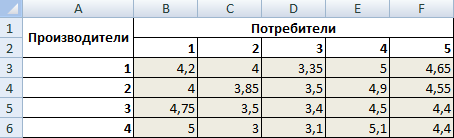
Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.

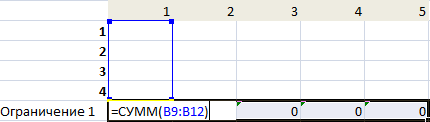
Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.

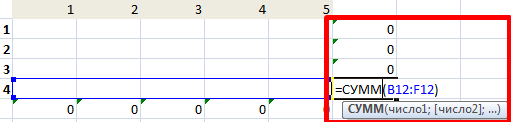
Вносим известные значения потребности в товаре и объема производства.

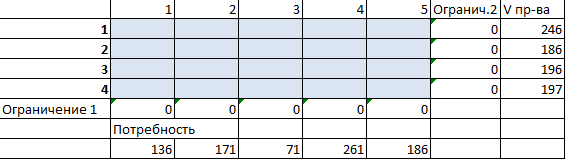
Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.

Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

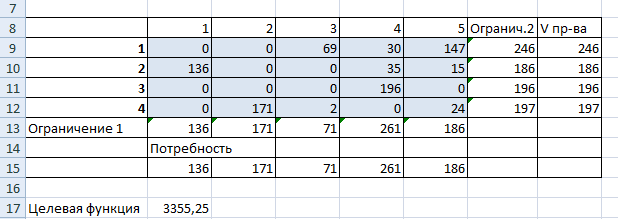
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Примеры решения сетевой транспортной задачи

Задача 7. Имеется сеть железных дорог, на которой расположены 3 пункта отправления однородного груза и 9 станций его приема. Известны затраты на перевозку грузов от i-ой до j-ой станции. Заданы объемы ресурсов в каждом пункте отправления и объемы прибытия в каждый пункт назначения. Требуется составить оптимальный план перевозок, предусматривающий минимальные суммарные затраты.1. Пункты 1, 2, 3 – пункты отправления с объемом запаса, соответственно 200, 150 и 150.Потребности пунктов назначения таковы: 4 – 40, 5 – 70, 6 – 40, 7 – 50, 8 – 45,9 – 60,10 – 70,11 – 75,12 – 50.Затраты между соответствующими вершинами заданы: 1-5 – 65, 1-7 – 75, 1-9 – 25, 2-5 – 60, 2-6 – 115, 2-9 – 25, 2-12 – 90, 3-4 – 95, 3-8 – 30, 3-10 – 45, 3-11 – 40, 4-8- 15, 4-12 – 40, 5-7 – 95, 5-9 – 35, 6-8 – 65, 6-9 – 15, 6-11 – 55,6-12 – 80,7-10 – 15,8-11 – 45,9-11 – 35,10-11-110.2. Пункты 1, 2, 3 – пункты отправления с объемом запаса, соответственно 200,150 и 150.Потребности пунктов назначения таковы: 4 – 40, 5 – 70, 6 – 40, 7 – 50, 8-45,9-60,10-70,11 -75,12-50.Затраты между соответствующими вершинами заданы: 1-5 – 65, 1-7 – 75, 1-9 – 25, 2-5 – 60, 2-6 – 115, 2-9 – 25, 2-12 – 90, 3-4 – 95, 3-8 – 30, 3-10 – 45, 3-11 – 40, 4-8 – 15, 4-12 – 40, 5-7 – 95, 5-9 – 35, 6-8 – 65, 6-9 – 15, 6-11 – 55,6-12 – 80,7-10 – 15,8-11 – 45, 9-11 – 35,10-11 -110.Для следующих звеньев существуют ограничения на пропускные способности. 1-7 – 40, 1-11 – 10, 2-9 – 15, 3-10 – 30.

Задача 8. Пункты производства и потребления связаны между собой транспортной сетью. В пунктах производства сосредоточено некоторое количество однородного груза, которое необходимо вывезти в пункты потребления. Стоимость перевозки единицы груза на каждом участке (равная Сs) задана. Предполагается, что на каждом участке перевозка грузов осуществляется в одном направлении. Требуется составить такой план перевозки, при котором транспортные расходы будут минимальными.

Транспортная задача с промежуточными пунктами

       В
транспортной сети, показанной на рисунке
2, осуществляются перевозки груза 
из пунктов 1 и 2 в пункты 5 и 6 через 
транзитные пункты 3 и 4. Стоимость перевозки 
единицы груза между пунктами
показана в таблице 3. Предложение 
пунктов 1, 2 (П1 и П2) и спрос пунктов
5,6 (С5 и С6) выбирается соответственно из
таблиц 4 и 5. Построить транспортную модель
с промежуточными пунктами. 

Рисунок 2 – Схема 
транспортной сети

Таблица 3 – Стоимость 
перевозки единицы груза между 

пунктами транспортной
сети                               

Поставщиики	Потребители
3	4	5	6
1	2	3	100	100
2	5	4	100	100
3	3	6	100
4	3	4	5
5	100	100	4

Таблица 4 – 
Предложение пунктов 1 и 2

Таблица 5 – Спрос пунктов
5 и 6

СПРОС ПУНКТА 5	155
СПРОС ПУНКТА 6	195

      2.1
Математическая постановка 
задачи

      Одно 
практически важное обобщение классической
транспортной задачи связано с учетом
возможности доставки товара от i-го
источника к j-му стоку по маршруту, проходящему
через некоторый промежуточный пункт
(склад). Так, например, промежуточные пункты
являются составной частью распределительной
системы любой крупной компании, имеющей
сеть универсальных магазинов во многих
городах

Такая компания обычно имеет
зональные оптовые базы (источники), снабжающие
товарами более мелкие региональные склады
(промежуточные пункты), откуда эти товары
поступают в розничную торговую сеть (стоки).
При этом товар для каждого фиксированного
стока в общем случае может быть доставлен
не из любого источника и по маршрутам,
не обязательно проходящим через все промежуточные
пункты. Кроме того, промежуточные пункты
могут обладать вполне определенной спецификой.
Так, например, при транспортировке товара
от источника к стоку по маршруту, проходящему
через склад, часть товара может быть использована
для создания неприкосновенного запаса
на складе.

S = 210 + Δ32 * 5 = 210 -4 * 5 = 190 ден. ед.

Полученное решение является оптимальным?
Проверим.
Каждому поставщику A _i ставим в соответствие некоторое число U _i , называемое потенциалом поставщика.
Каждому потребителю B _j ставим в соответствие некоторое число V _j , называемое потенциалом потребителя.

Для задействованного маршрута:потенциал поставщика + потенциал потребителя = тариф задействованного маршрута.
Последовательно найдем значения потенциалов.
Значение одного потенциала необходимо задать. Пусть u₁ = 0.

A1B1 :   v1 + u1 = 4     v1 = 4 — 0 = 4 A1B2 :   v2 + u1 = 5     v2 = 5 — 0 = 5 A2B2 :   v2 + u2 = 2     u2 = 2 — 5 = -3 A2B3 :   v3 + u2 = 1     v3 = 1 — (-3) = 4 A3B2 :   v2 + u3 = 1     u3 = 1 — 5 = -4 A3B4 :   v4 + u3 = 2     v4 = 2 — (-4) = 6 A4B4 :   v4 + u4 = 0     u4 = 0 — 6 = -6

Поставщик   Потребитель   U   B 1 B 2 B 3 B 4 A 1 20 4 10 5 3 6   u1 = 0   A 2 7 2 25 1 5   u2 = -3   A 3 6 5 1 4 15 2   u3 = -4   A 4 5   u4 = -6     V   v1 = 4 v2 = 5 v3 = 4 v4 = 6

Найдем оценки незадействованных маршрутов (cij — стоимость доставки). ? A1B3 :   Δ13 = c13 — ( u1 + v3 ) = 3 — ( 0 + 4 ) = -1 A1B4 :   Δ14 = c14 — ( u1 + v4 ) = 6 — ( 0 + 6 ) = A2B1 :   Δ21 = c21 — ( u2 + v1 ) = 7 — ( -3 + 4 ) = 6 A2B4 :   Δ24 = c24 — ( u2 + v4 ) = 5 — ( -3 + 6 ) = 2 A3B1 :   Δ31 = c31 — ( u3 + v1 ) = 6 — ( -4 + 4 ) = 6 A3B3 :   Δ33 = c33 — ( u3 + v3 ) = 4 — ( -4 + 4 ) = 4 A4B1 :   Δ41 = c41 — ( u4 + v1 ) = 0 — ( -6 + 4 ) = 2 A4B2 :   Δ42 = c42 — ( u4 + v2 ) = 0 — ( -6 + 5 ) = 1 A4B3 :   Δ43 = c43 — ( u4 + v3 ) = 0 — ( -6 + 4 ) = 2

Есть отрицательная оценка. Следовательно, возможно получить новое решение, как минимум, не хуже имеющегося.
ШАГ №2.

Выберем ячейку A₁B₃, ее оценка отрицательная.
Пожалуйста, поставьте курсор мыши в выбранную ячейку A₁B₃Используя только горизонтальные и вертикальные перемещения курсора, соедините непрерывной линией заполненные ячейки так, чтобы вернуться в исходную ячейку A₁B₃
Ячейки, расположенные в вершинах построенной ломаной линии, образуют цикл для выбранной ячейки(см. выделенные ячейки в таблице ниже).
Он единственный.
Направление обхода не имеет значения.

Поставщик	Потребитель	Запас
B 1	B 2	B 3	B 4
A 1	20 4	10 5	-1 3	6	30
A 2	7	2	25 1	5	25
A 3	6	5 1	4	15 2	20
A 4	5	5
Потребность	20	15	25	20

10 = min { 10, 25 } ?

Поставщик	Потребитель	Запас
B 1	B 2	B 3	B 4
A 1	20 4	10 5	-1 3	6	30
A 2	7	2	25 1	5	25
A 3	6	5 1	4	15 2	20
A 4	5	5
Потребность	20	15	25	20

Данное преобразование не изменит баланса.
А вот общая стоимость доставки продукции изменится на величину:

3 * 10 — 5 * 10 + 2 * 10 — 1 * 10 = ( 3 — 5 + 2 — 1 ) * 10 = -1 * 10 ден. ед.Вы правильно заметили, что -1 * 10 = Δ₁₃ * 10 ?

Поставщик	Потребитель	Запас
B 1	B 2	B 3	B 4
A 1	20 4	10 — 10 5	+10 -1 3	6	30
A 2	7	0 + 10 2	25 — 10 1	5	25
A 3	6	5 1	4	15 2	20
A 4	5	5
Потребность	20	15	25	20

Получили новое решение. ?

Поставщик	Потребитель	Запас
B 1	B 2	B 3	B 4
A 1	20 4	5	10 3	6	30
A 2	7	10 2	15 1	5	25
A 3	6	5 1	4	15 2	20
A 4	5	5
Потребность	20	15	25	20

Общую сумму доставки продукции, для данного решения, легко посчитать.

Пример решения транспортной задачи в Excel

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
2. Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
3. Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
4. Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
5. Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
6. Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
7. Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
8. Копируем маркером заполнения формулу на всю строку.
9. Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
10. Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
11. Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
12. Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
13. После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

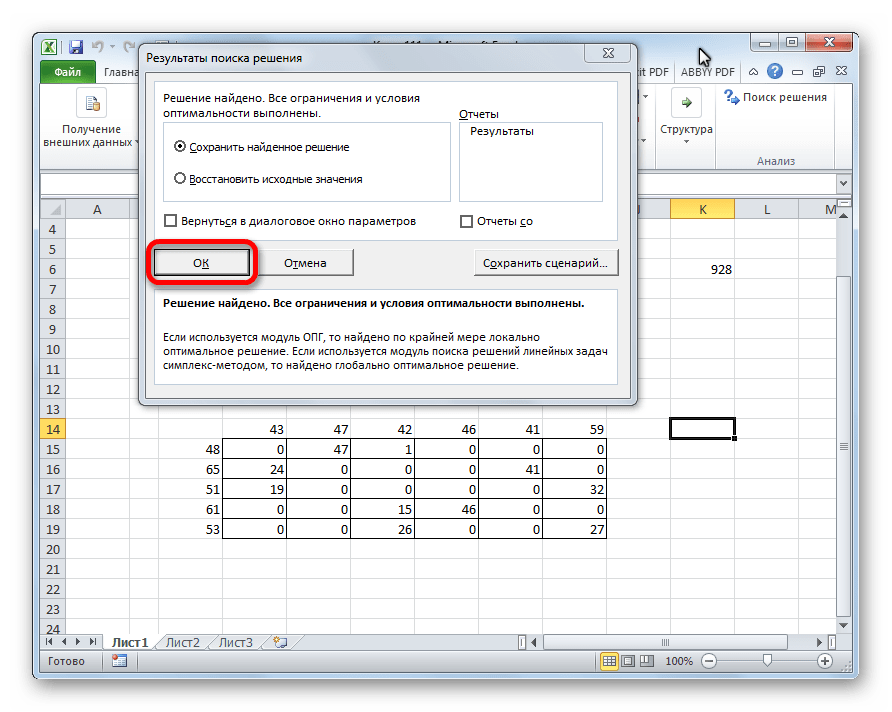
Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Решение классической транспортной задачи в Excel

Рассмотрим решение классической транспортной задачи на основе примера заимствованного из книги .

Задача 2. Для перевозки продовольственных грузов имеется три оптово-розничных склада № 1, № 2 и № 3 и два магазина № 1 и № 2. Объемы перевозки грузов составят соответственно 1000, 1500 и 1200 кг. Ежедневная потребность магазинов (распределительных центров) составляет 2300 и 1400 кг товара. Расстояние (в км) между заводами и распределительными центрами приведены в табл. 2.1.

Мощность грузопотоков

Транспортная компания оценивает свои услуги в 1 копейку за перевозку одного кг груза на один км. В результате получаем представленную в табл. 2.2 стоимость перевозок (в рублях) по каждому маршруту.

Стоимость перевозки товаров

Основываясь на данных из табл. 2.2, формулируем следующую задачу линейного программирования.

x_ij0, i=1,2,3, j=1,2.

Эти ограничения выражены в виде равенств, поскольку общий объем перевезенных грузов со складов (S=1000+1500+1200=3700) равен суммарному спросу магазинов (D=2300+1400=3700).

Данную задачу можно решить с помощью так называемой транспортной таблицы. Решение данной задачи в Excel представлено на рис. 2.2 — 2.4.

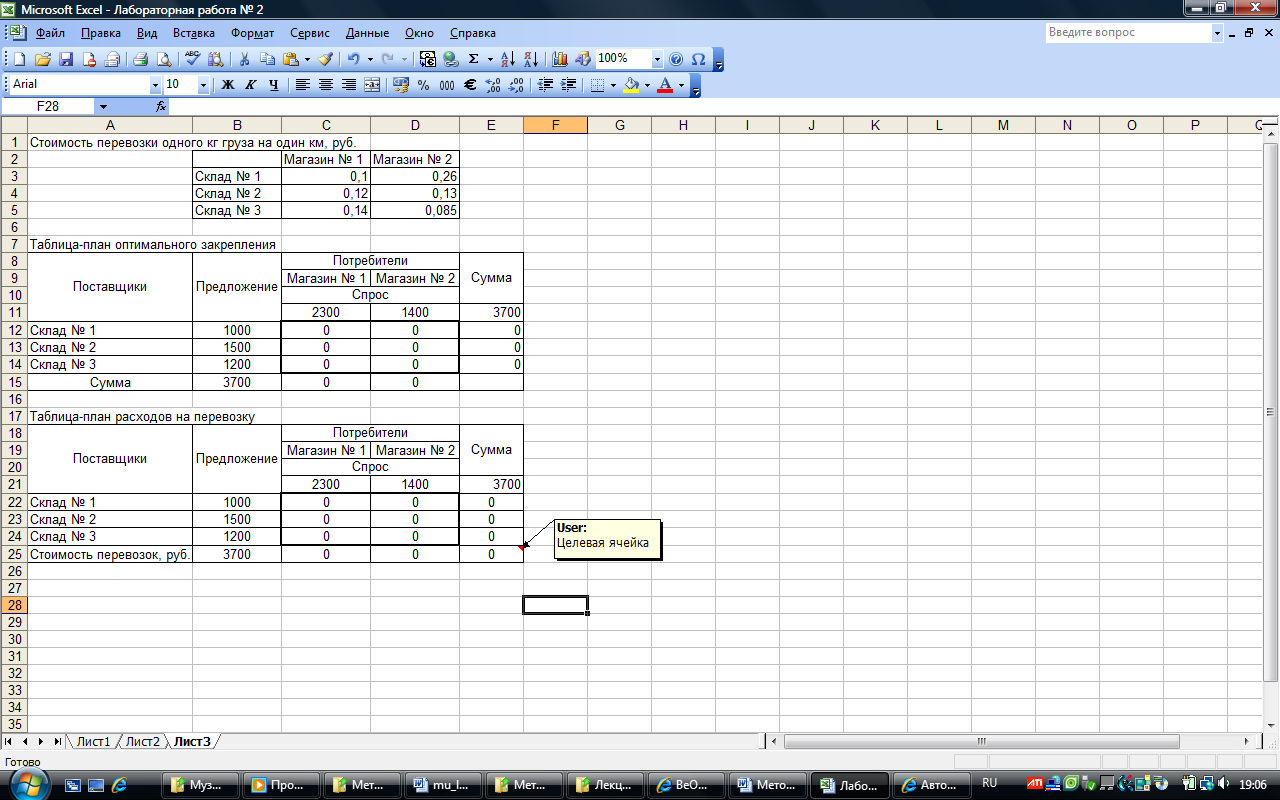
Рис. 2.2. Таблицы решения транспортной задачи

Исходные данные для решения классической транспортной задачи целесообразно представить в виде трех таблиц (см. рис. 2.2), в первой из которых представлены значения стоимости перевозок единицы товара c_ij от i-го поставщика к j-му потребителю.

Заполняем таблицу Стоимость перевозки одного кг груза на один км, руб. (рис. 2. 1).

Во второй таблице представлены: значения S_i предложения каждого i-го поставщика; значения D_j спроса каждого _j-го потребителя; переменные x_ij, первоначально принимающие нулевые значения; вспомогательная строка и вспомогательный столбец «Сумма».

Далее заполняем графы Таблицы-плана оптимального закрепления (рис. 2.2).

Ниже формируем Таблицу-план расходов на перевозку. Пересечения столбцов и строк представляют собой произведения соответствующих ячеек двух предыдущих таблиц.

Целевая ячейка Е25 должна содержать формулу, выражающую целевую функцию:

= СУММ(C22:D24)

Используя меню СервисПоиск решения открываем диалоговое окно Поиск решения (см. рис. 2.3), в котором устанавливаем целевую ячейку равной минимальному значению, определяем диапазон изменяемых ячеек и ограничения и запускаем процедуру вычисления, щелкнув по кнопке Выполнить.

Рис. 2.3. Окно поиска решения

Оптимальное решение данной задачи представлено на рис. 2. 4. Оно предполагает перевозку 1000 кг товара со склада №1 до магазина № 1, 1300 кг – со склада № 2 до магазина № 1, 200 кг товара со склада № 2 до магазина № 2 и 1200 кг товара со склада № 3 до магазина № 2. Минимальная стоимость перевозок составляет 384 рубля.

Рис. 2.4. Оптимальное распределение товара по маршрутам

Когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами назначения, транспортная задача называется несбалансированной. В этом случае, при решении классической транспортной задачи методом потенциалов, применяют прием, позволяющий несбалансированную транспортную задачу сделать сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц. В Excel несбалансированная транспортная задача решается путем изменения ограничений по спросу (если спрос превышает предложение) или по предложению (если предложение превышает спрос), т.е. система ограничений будет иметь вид:

в первом случае, либо

во втором случае.

При решение несбалансированной транспортной задачи в Excel, в отличии от вышеприведенного примера в окне поиска решения приведено ниже. Оно заключается в определении ограничений для поиска решения.

Например, уменьшив потребный объем перевозок для первого магазина до 2000 кг, мы получим результат решения, аналогичный приведенному на рисунке ниже. На этом же рисунке приведены ограничения, накладываемые для поиска решения.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

Решим транспортную задачу методом потенциалов. Нам известны торговые запасы, потребительские запросы и стоимость доставки за единицу продукции. Сделаем три исходные таблицы.

Построим опорный план транспортной задачи с помощью инструмента «Поиск решений». Рядом составим такие же по объему таблицы с пустыми ячейками. Таблица А – аналог стоимостной, Б – «запасов», В – «спроса».

Элементы таблицы Б – сумма соответствующих строк в таблице А. Элементы таблицы В – сумма соответствующих столбцов в таблице А.

Отдельно составим результирующую таблицу Г. В ней отразятся оптимальные транспортные расходы. Каждый элемент таблицы Г – произведение элемента А и соответствующего элемента стоимостной таблицы.

В отдельном месте листа введем формулу функции: =СУММПРОИЗВ(A1:C3;G1:I3)

Первый массив – стоимостная таблица, второй – диапазон А.

Ставим курсор в ячейку со значением функции. Вызываем инструмент «Поиск решения». Заполняем диалоговое окно:

1. Целевая ячейка – ссылка на ячейку со значением функции.
2. Она должна быть равна «максимальному значению», как наиболее выгодному для перевозчика.
3. Команда изменяет значения ячеек в таблице А. Значения – целые числа.
4. Диапазон таблицы Б = «Запасам».
5. Диапазон В = «Потребительскому спросу».

В открытом диалоговом окне нажимаем кнопку «Параметры» и устанавливаем следующие настройки:

Жмем ОК – «Выполнить». Получаем опорный план транспортной задачи:

Он залит бледно-зеленым цветом. Ячейки со значениями выше нуля называются «базисными», «занятыми». Ячейки со значением 0 – «свободными».

Далее действуем по плану:

Посчитаем число занятых клеток с помощью функции СЧЕТЕСЛИ.

Так как результат равен 5, опорный план является не вырожденным. Проверим оптимальность опорного плана – найдем потенциалы по занятым клеткам.

Нужно составить систему уравнений. Предполагается, что αj = 0, а αi + βj = сij (стоимость доставки единицы груза). Вызываем команду «Поиск решения». Вносим условия системы уравнений в качестве ограничений.

Заполненное диалоговое окно:

Результат работы инструмента «Поиск решения»:

Посчитаем оценки свободных клеток. Формула: сij – (αi + βj). Берем свободную клетку из таблицы А. Смотрим ее значение в стоимостной таблице. Это будет сij. Далее смотрим, какие потенциалы соответствуют данной клетке. Вставляем их значения в формулу.

В программе Excel найдем оценки с помощью математических операторов и ссылок на соответствующие ячейки.

План считается оптимальным, если оценки больше или равны 0. В нашем случае получились отрицательные значения – план не является оптимальным. Поэтому двигаемся дальше.

Находим, какой клетке в таблице А соответствует минимальная оценка. Строим для этой клетки цикл – замкнутую ломаную линию. Условия: обязательно чередование вертикального и горизонтального направления, только по базисным клеткам.

В исходной клетке (с минимальной оценкой) ставим знак «+». Далее чередуем: «-», «+» и т.д.

В таблице стоимости находим минимальное значение со знаком «-».

В нашем примере – это «5», ячейка В1. Эту клетку нужно убрать из базиса. А ячейку с минимальной оценкой сделать базисной.

С учетом изменившихся данных вновь строим опорный план транспортной задачи. Применяем инструмент «Поиск решения». Пересчитанный план перевозок выглядит так:

Обратите внимание: ячейка I1 (где была минимальная оценка) стала базисной, занятой. Проводим те же расчеты для нового плана (с пункта №1): находим потенциалы, оценки свободных клеток для проверки оптимальности. И так до тех пор, пока оценки свободных клеток не будут больше или равны 0

И так до тех пор, пока оценки свободных клеток не будут больше или равны 0

Проводим те же расчеты для нового плана (с пункта №1): находим потенциалы, оценки свободных клеток для проверки оптимальности. И так до тех пор, пока оценки свободных клеток не будут больше или равны 0.

Полученное решение сохраняется в файле Word (Пример решения транспортной задачи). Также автоматически генерируется шаблон решения в Excel .

Решение матричной игрыС помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

Задачи динамического программирования

• вычеркивания (метод двойного предпочтения);
• северо-западного угла;
• минимального элемента;
• аппроксимации Фогеля.