Как в excel построить тренд

Способ отсчета времени от условного начала

Пример
. Статистическое изучение динамики численности населения.

1. С помощью цепных, базисных, средних показателей динамики оцените изменение численности, запишите выводы.
2. С помощью метода аналитического выравнивания (по прямой и параболе, определив коэффициенты с помощью МНК) выявите основную тенденцию в развитии явления (численность населения Республики Коми). Оцените качество полученных моделей с помощью ошибок и коэффициентов аппроксимации.
3. Определите коэффициенты линейного и параболического трендов с помощью средств «Мастера диаграмм». Дайте точечный и интервальный прогнозы численности на 2010 г. Запишите выводы.

1990	1996	2001	2002	2003	2004	2005	2006	2007	2008
1249	1133	1043	1030	1016	1005	996	985	975	968

ТОП 5 лучших функций Excel для экономиста

Доброго времени суток уважаемый читатель!

Эту статью я хочу посвятить экономистам и их работе, точнее говоря тем инструментам, которые им очень нужны в работе и позволят значительно сократить свои усилия, сэкономят ваше время и улучшат ваши результаты.

Несмотря на всё то многообразие функций, которые существует в Excel, тем не менее, есть основная когорта функций, знать которые необходимо каждому уважающему себя и свой труд экономисту. Да именно экономисту, человеку с которого реально начинается работа предприятия, ведь исходя из его планирования и расчётов действует предприятие, они решают, как и что надо делать, что бы получить позитивные экономический эффект. Конечно, многие могут, не согласится с моими словами, но я говорю исходя из собственного опыта и взглядов, а они у каждого разные.

Я сомневаюсь что многие будут со мной спорить в том вопросе что знать экономический эффект от любого действия на предприятии или рассчитать прибыль для любого продукта это «архиважно» товарищи. А вот для этого и важны те функции, которые мы будем рассматривать

Рассмотрим 5 ТОП функций для экономиста, это:

Как улучшить коэффициент достоверности аппроксимации в Excel?

Коэффициент достоверности аппроксимации — это важный инструмент для оценки точности аппроксимирующей функции в Excel. Чтобы улучшить его значение, необходимо понимать, как она рассчитывается.

Один из способов улучшения коэффициента достоверности аппроксимации — проверка выбранной функции на соответствие типу данных, которые используются в таблице. Если данные не соответствуют типу функции, то коэффициент достоверности аппроксимации будет низок. Например, при использовании линейной функции для квадратичных данных. В таком случае нужно выбрать функцию, которая соответствует данным.

Другой способ улучшения коэффициента достоверности аппроксимации — выбор оптимального числа точек для аппроксимации. Аппроксимация на небольшом числе точек может дать неверный результат. Поэтому следует использовать достаточное число точек, чтобы получить наиболее точную функцию.

Также необходимо проводить анализ данных на выбросы и аномалии, которые могут повлиять на точность и достоверность аппроксимации. Их можно удалить или откорректировать, чтобы получить более точные результаты.

В Excel доступны множество функций аппроксимации, которые могут помочь улучшить коэффициент достоверности. Их выбор зависит от типа данных, которые используются

Что касается конкретных операций по улучшению коэффициента достоверности аппроксимации, то важно применять их на основе анализа ситуации в конкретном случае

Создание графика

Excel предоставляет возможность создавать различные графики для наглядной визуализации данных. Для создания графика в Excel следуйте следующим шагам:

1. Выберите диапазон ячеек, которые вы хотите отобразить на графике.
2. Перейдите на вкладку «Вставка» в верхней панели инструментов.
3. Выберите тип графика, который соответствует вашим потребностям. Например, вы можете выбрать столбчатую диаграмму, круговую диаграмму, линейный график и т. д.
4. После выбора типа графика выберите одну из представленных вариантов графиков, чтобы применить его к вашим данным.
5. Если необходимо, вы можете настроить внешний вид графика, добавить название осей, заголовок графика или легенду. Для этого используйте доступные инструменты в Excel.
6. Готово! Ваш график будет автоматически создан на выбранной вами вкладке.

Созданный график можно также редактировать, изменять тип графика, добавлять новые данные и многое другое. Для этого просто выделите график и воспользуйтесь панелью инструментов для редактирования графиков.

Excel предоставляет широкие возможности для создания и настройки графиков, что позволяет представлять данные в удобной и понятной форме.

Функция СУММПРОИЗВ в Excel

Пятой функцией нашего топ-списка станет функция СУММПРОИЗВ, которая является, наверное, даже наиглавнейшей функцией для экономиста. Она позволяет воплотить в себе практически все предыдущее возможности, которые имеют функции ЕСЛИ, СУММЕСЛИ, СУММЕСЛИМН, а также производить свои вычисление в 255 массивах, а это, я вам скажу, ох как много.

Функция СУММПРОИЗВ в Excel позволит вам справится практически с любой экономической задачей, где фигурируют массивы. Подобрав правильные критерии или условия, с помощью формул или иным способом, любые задачи смогут капитулировать перед легкостью, с которой эта функция будет их решать.

Не стоит заблуждаться ее кажущейся простотой или запутанным описанием, это отличный инструмент о котором вы должны знать и уметь им пользоваться, это сократить ваше время и сбережёт километры нервных клеток.

Детально о том, как работает функция СУММПРОИЗВ в Excel вы можете ознакомиться здесь.

А на этом у меня всё! Я очень надеюсь, что список самых важных ТОП-5 функций для экономиста или бухгалтера мы рассмотрели . Буду очень благодарен за оставленные комментарии, так как это показатель читаемости и вдохновляет на написание новых статей! Делитесь с друзьями прочитанным и ставьте лайк!

Не забудьте поблагодарить автора!

То не беда, если за рубль дают полрубля; а то будет беда, когда за рубль станут давать в морду. Михаил Салтыков-Щедрин

Урок 4. Виды аппроксимации в Excel

Текст урока с работающими фрагментами расчетов в файле uroki-approksimacii.xls

Как и предыдущие, этот урок с аналогичным текстом лучше смотреть не листе Excel (см. Уроки аппроксимации.xls, Лист1)

Аппроксимация в Excel проще всего реализуется с помощью программы построения трендов. Для выяснения особенностей аппроксимации возьмем какой-либо конкретный пример. Например, энтальпию насыщенного пара по книге С.Л.Ривкина и А.А.Александрова «Теплофизические свойства воды и водяного пара», М., «Энергия», 1980г. В колонке P поместим значения давления в кгс/см2, в колонке i» — энтальпию пара на линии насыщения в ккал/кг и построим график с помощью опции или кнопки «Мастер диаграмм».

Щелкнем правой кнопкой по линии на рисунке, затем левой кнопкой по опции «Добавить линию тренда» и смотрим — какие услуги предлагаются нам этой опцией в части реализации аппроксимации в Excel.

Нам предлагается на выбор пять типов аппроксимации: линейная, степенная, логарифмическая, экспоненциальная и полиноминальная. Чем они хороши и чем могут нам помочь? — Нажимаем кнопку F1, затем щелкаем по опции «Мастер ответов» и в появившееся окошко вводим нужное нам слово «аппроксимация», после чего щелкаем по кнопке «Найти». Выбираем в появившемся списке раздел «Формулы для построения линий тренда».

Получаем следующую информацию в несколько измененной нами

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где b — угол наклона и a — координата пересечения оси абсцисс (свободный член).

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где c и b — константы.

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где a и b — константы.

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где b и k — константы.

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где a, b1, b2, b3. b6 — константы.

Снова щелкаем по линии рисунка, затем по опции «Добавить линию тренда», далее по опции «Параметры» и ставим флажки в окошках слева от записей: «показывать уравнение на диаграмме» и «поместить на диаг- рамму величину достоверности аппроксимации R^2, после чего щелкаем по кнопке OK. Пробуем все варианты аппроксимации по порядку.

Линейная аппроксимация дает нам R^2=0.9291 — это низкая достоверность и плохой результат.

Для перехода к степенной аппроксимации щелкаем правой кнопкой по линии тренда, затем левой кнопкой — по опции «Формат линии тренда», далее по опциям «Тип» и «Степенная». На этот раз получили R^2=0.999.

Запишем уравнение линии тренда в виде, пригодном для расчетов на листе Excel:

В результате имеем:

Максимальная погрешность аппроксимации получилась на уровне 0.23 ккал/кг. Для аппроксимации экспериментальных данных такой результат был бы чудесным, но для аппроксимации справочной таблицы это не слишком хороший результат. Поэтому попробуем проверить другие варианты аппроксимации в Excel посредством программы построения трендов.

Логарифмическая аппроксимация дает нам R^2=0.9907 — несколько хуже, чем по степенному варианту. Экспоненнта в том варианте, который предлагает программа построения трендов, вообще не подошла — R^2=0.927.

Полиноминальная аппроксимация со степенью 2 (это y=a+b1*x+b2*x^2) обеспечила R^2=0.9896. При степени 3 получили R^2=0.999, но с явным искажением аппроксимируемой кривой, в особенности при P>0.07 кгс/см2. Наконец, пятая степень нам дает R^2=1 — это, как утверждается, максимально тесная связь между исходными данными и их аппроксимацией.

Перепишем уравнение полинома в пригодном для расчетов на листе Excel виде:

и сравним результат аппроксимации с исходной таблицей:

Оказалось, что R^2=1 в данном случае лишь блестящая ложь. Реально, самый лучший результат полиноминальной аппроксимации дал самый простой полином вида y=a+b1*x+b2*x^2. Но его результат хуже, чем в варианте степенной аппроксимации y=634.16*x^0.012, где максимальная погрешность аппроксимации находилась на уровне 0.23 ккал/кг. Это все, что мы можем выжать из программы построения трендов. Посмотрим, что мы можем выжать из функции Линейн. Для нее попробуем вариант степенной аппроксимации.

Примечание. Обнаруженный дефект связан с работой программы построения трендов, но не с методом МНК.

Что такое аппроксимация в Excel и для чего она нужна

Аппроксимация — это процесс поиска функции, которая приближает набор данных или экспериментальные результаты. В контексте Excel аппроксимация обычно используется для нахождения математической модели, которая описывает зависимость между двумя или более переменными.

При помощи аппроксимации в Excel вы можете:

• Выразить сложные данные или результаты экспериментов в виде простой математической формулы.
• Предсказать значения переменных вне известного диапазона данных.
• Оптимизировать параметры модели, чтобы достичь наилучшего соответствия данным.
• Использовать полученную модель для анализа и прогнозирования будущих значений.

Excel предлагает несколько функций и инструментов для выполнения аппроксимации:

1. Линейная регрессия: Эта функция позволяет вам найти линейную связь между двумя переменными. Вы можете использовать ее, когда данные приближаются к прямой линии.
2. Полиномиальная регрессия: Эта функция позволяет вам найти нелинейную связь между переменными, используя полиномиальную модель. Вы можете использовать ее, когда данные приближаются к кривой линии.
3. Экспоненциальная регрессия: Эта функция позволяет вам найти экспоненциальную связь между переменными. Вы можете использовать ее, когда данные приближаются к экспоненциальной кривой.
4. Логарифмическая регрессия: Эта функция позволяет вам найти логарифмическую связь между переменными. Вы можете использовать ее, когда данные приближаются к логарифмической кривой.

Аппроксимация в Excel может быть полезна во многих областях, таких как наука, инженерия, финансы и экономика. Она позволяет анализировать имеющиеся данные, делать прогнозы и принимать обоснованные решения на основе полученных результатов.

Как подогнать кривую

Чтобы подогнать кривую под наши данные, мы выполняем следующие шаги:

Выберите данные для нашего графика, B2:C17, который представляет собой табличный результат взаимосвязи между температурой и объемом.

Рисунок 2. Пример данных для аппроксимации кривой

Рисунок 3. Вариант точечной диаграммы

• Будет создана точечная диаграмма, а вкладка Дизайн появится на панели инструментов в разделе Инструменты для работы с диаграммами.
• Нажмите Добавить элемент диаграммы Линия тренда Дополнительные параметры линии тренда

Рисунок 4. Добавление параметров линии тренда

• В окне Формат линии тренда выберите Полиномиальный и установите для параметра Порядок значение «2»
• Отметьте параметр «Отображать уравнение на диаграмме».

Рис. 5. Диалоговое окно «Формат линии тренда»

Excel мгновенно добавит наиболее подходящую кривую для наших данных и отобразит полиномиальное уравнение на диаграмме. Мы можем добавить значение R-квадрата в качестве меры того, насколько близки наши точки данных к линии регрессии. Нам просто нужно установить флажок «Отображать значение R-квадрата на графике».

При подборе кривой мы хотим, чтобы значение R-квадрата было как можно ближе к значению 1. На изображении ниже показан наш точечный график с полиномиальной линией тренда порядка 2. Значение R-квадрата равно «0,9759».

Рисунок 6. Вывод: Как подогнать кривую

Аппроксимация в Excel

Учет и контроль! Те, кому за 40 должны хорошо помнить этот лозунг из эпохи построения социализма и коммунизма в нашей стране.

Но без хорошо налаженного учета невозможно эффективное функционирование ни страны, ни области, ни предприятия, ни домашнего хозяйства при любой общественно-экономической формации общества! Для составления прогнозов и планов деятельности и развития необходимы исходные данные. Где их брать? Только один достоверный источник – это ваши статистические учетные данные предыдущих периодов времени.

Учитывать результаты своей деятельности, собирать и записывать информацию, обрабатывать и анализировать данные, применять результаты анализа для принятия правильных решений в будущем должен, в моем понимании, каждый здравомыслящий человек. Это есть ничто иное, как накопление и рациональное использование своего жизненного опыта. Если не вести учет важных данных, то вы через определенный период времени их забудете и, начав заниматься этими вопросами вновь, вы опять наделаете те же ошибки, что делали, когда впервые этим занимались.

«Мы, помню, 5 лет назад изготавливали до 1000 штук таких изделий в месяц, а сейчас и 700 еле-еле собираем!». Открываем статистику и видим, что 5 лет назад и 500 штук не изготавливали…

«Во сколько обходится километр пробега твоего автомобиля с учетом всех затрат?» Открываем статистику – 6 руб./км. Поездка на работу – 107 рублей. Дешевле, чем на такси (180 рублей) более чем в полтора раза. А бывали времена, когда на такси было дешевле…

«Сколько времени требуется для изготовления металлоконструкций уголковой башни связи высотой 50 м?» Открываем статистику – и через 5 минут готов ответ…

«Сколько будет стоить ремонт комнаты в квартире?» Поднимаем старые записи, делаем поправку на инфляцию за прошедшие годы, учитываем, что в прошлый раз купили материалы на 10% дешевле рыночной цены и – ориентировочную стоимость мы уже знаем…

Ведя учет своей профессиональной деятельности, вы всегда будете готовы ответить на вопрос начальника: «Когда. ». Ведя учет домашнего хозяйства, легче спланировать расходы на крупные покупки, отдых и прочие расходы в будущем, приняв соответствующие меры по дополнительному заработку или по сокращению необязательных расходов сегодня.

В этой статье я на простом примере покажу, как можно обрабатывать собранные статистические данные в Excel для возможности дальнейшего использования при прогнозировании будущих периодов.

Что разъясняет регрессия?

До этого, чем мы приступим к рассмотрению функций MS Excel, позволяющих, решать данные задачки, хотелось бы для вас на пальцах разъяснить, что, в сути, подразумевает регрессионный анализ. Так для вас проще будет сдавать экзамен, а самое основное, интересней учить предмет.

Будем надежды, вы знакомы с понятием функции из арифметики. Функция – это связь 2-ух переменных. При изменении одной переменной что-то происходит с иной. Изменяем X, изменяется и Y, соответственно. Функциями описываются разные законы. Зная функцию, мы можем подставлять произвольные значения X и глядеть на то, как при всем этом поменяется Y.

Это имеет огромное значение, так как регрессия – это попытка разъяснить при помощи определённой функции на 1-ый взор бессистемные и беспорядочные процессы. Так, к примеру, можно выявить связь курса бакса и безработицы в Рф.

Если данную закономерность найти получится, то по приобретенной нами в процессе расчетов функции, мы сможем составить прогноз, какой будет уровень безработицы при N-ом курсе бакса по отношению к рублю. Данная связь будет называться корреляцией. Регрессионный анализ подразумевает расчет коэффициента корреляции, который растолкует тесноту связи меж рассматриваемыми нами переменными (курсом бакса и числом рабочих мест).

Данный коэффициент быть может положительным и отрицательным. Его значения находятся в границах от -1 до 1. Соответственно, мы может следить высшую отрицательную либо положительную корреляцию. Если она положительная, то за повышением курса бакса последует и возникновение новейших рабочих мест. Если она отрицательная, означает, за повышением курса, последует уменьшение рабочих мест.

Регрессия бывает нескольких видов. Она быть может линейной, параболической, степенной, экспоненциальной и т.д. Выбор модели мы делаем зависимо от того, какая регрессия будет соответствовать непосредственно нашему случаю, какая модель будет очень близка к нашей корреляции. Разглядим это на примере задачки и решим её в MS Excel.

Сортировка с одним условием (по возрастанию/убыванию)

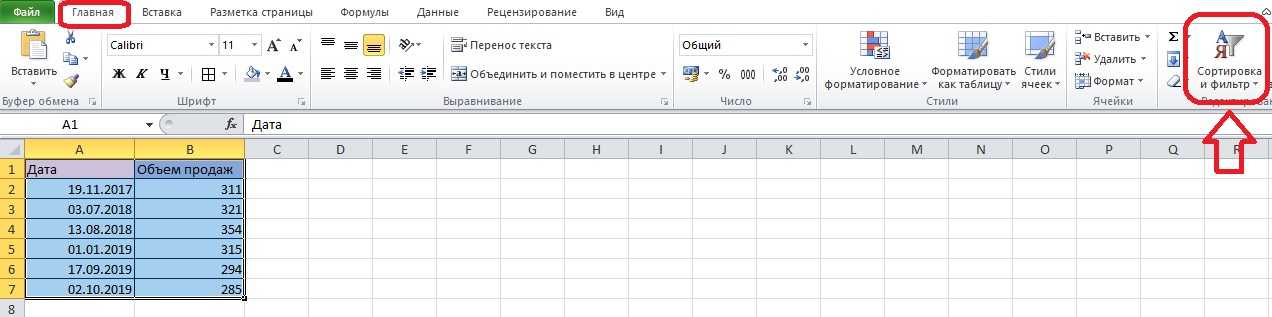
Этот метод сортировки по дате – самый простой. Для него требуются только опции панели инструментов. Составим таблицу, где важную роль играют даты. Следует указать полное обозначение – день, месяц и год. Сортировка с наибольшей вероятностью сработает правильно, если информация указана в таком формате.

1. Выбираем одну из заполненных ячеек и переходим на вкладку «Главная». Справа вверху появится кнопка «Сортировка и фильтр» – нажмите ее, чтобы открыть меню.

1

2. В появившемся списке есть два пункта сортировки по датам. Строки можно разместить в порядке от старых к новым или от новых к старым. Представим, что нам требуется порядок от ранних дат к поздним. Выбираем пункт «От старых к новым».

2

3. Теперь даты в таблице расположены в порядке от 2017-го года до 2019-го года.

3

4. Попробуем поставить записи в обратном порядке. Снова выбираем любую ячейку из диапазона и запускаем «Сортировку от новых к старым» из опций сортировки. Строки меняются местами – сейчас объемы продаж за 2019 год находятся выше.

4

Разбор результатов анализа

Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.

Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.

Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.

Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.

Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.

Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.

нескольких независимых

Уравнение линии тренда в Excel

В приведенном выше примере линейная аппроксимация выбрана только для иллюстрации алгоритма. Значение R-квадрата показывает, что выбор не удался.

Необходимо выбрать такой тип представления, который лучше всего иллюстрирует тенденцию изменения данных, вводимых пользователем. Давайте рассмотрим варианты.

Линейная аппроксимация

Его геометрическое представление — прямая линия. Следовательно, линейная аппроксимация используется для иллюстрации индикатора, который увеличивается или уменьшается с постоянной скоростью.

Рассмотрим условное количество договоров, заключенных менеджером на 10 месяцев:

На основе данных электронной таблицы Excel составьте точечную диаграмму (это поможет проиллюстрировать линейный тип):

Получаем результат:

Обратите внимание, что в линейном типе аппроксимации точки данных расположены очень близко к линии. Этот тип использует следующее уравнение:. y = 4 503 x + 6 1333

y = 4 503 x + 6 1333

• где 4,503 – показатель уклона;
• 6,1333 – смещение;
• y — последовательность значений,
• x — номер периода.

Прямая линия на графике показывает неуклонный рост качества работы менеджера. Значение R-квадрата равно 0,9929, что свидетельствует о хорошем согласии расчетной прямой с исходными данными. Прогнозы должны быть точными.

Чтобы спрогнозировать количество заключенных договоров, например, в периоде 11, необходимо вместо x в уравнении поставить число 11. После подсчета выясняем, что в 11 периоде менеджер заключит 55-56 договоров.

Экспоненциальная линия тренда

Этот тип полезен, если входные значения изменяются с увеличением скорости. Экспоненциальная аппроксимация не применяется при нулевых или отрицательных характеристиках.

Давайте создадим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения электроснабжения в районе X:

Уравнение выглядит следующим образом:

• 7,6403 и -0,084 – константы;
• e – основание натурального логарифма.

Показатель R-квадрата равен 0,938, что означает, что кривая соответствует данным, ошибка минимальна, и прогнозы будут точными.

Логарифмическая линия тренда и прогноз продаж

Применяется для следующих изменений показателя: сначала быстрый рост или снижение, затем — относительная стабильность. Оптимизированная кривая хорошо адаптируется к этому значению «поведения». Логарифмический тренд подходит для прогнозирования продаж нового продукта, только что вышедшего на рынок.

Первоначальная задача производителя – расширить клиентскую базу. Когда товар найдет своего покупателя, его нужно будет удержать и обслужить.

Создайте диаграмму и добавьте логарифмическую линию тренда для условного прогноза продаж продукта:

R2 по значению близок к 1 (0,9558), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объем продаж на последующие периоды. Для этого вместо x в уравнении подставьте номер периода.

Для расчета прогнозных значений используется формула: =304,52*LN(A18)+101,57, где A18 – номер периода.

Полиномиальная линия тренда в Excel

Эта кривая показывает попеременное увеличение и уменьшение. Для многочленов определяется степень (по количеству минимального и максимального значений). Например, одна крайность (минимум и максимум) — это вторая степень, две крайности — третья степень, три крайности — четвертая.

Полиномиальный тренд в Excel используется для анализа большого набора данных с нестабильными значениями. Давайте рассмотрим пример первого набора значений (цены на нефть).

Когда у нас есть набор данных и мы хотим определить взаимосвязь между переменными с помощью регрессионного анализа, мы можем создать кривую, которая лучше всего соответствует нашим точкам данных. К счастью, Excel позволяет подобрать кривую и составить уравнение, представляющее наилучшую кривую.

Рисунок 1. Окончательный результат: Аппроксимация кривой

Аппроксимация в Excel статистических данных аналитической функцией.

Производственный участок изготавливает строительные металлоконструкции из листового и профильного металлопроката. Участок работает стабильно, заказы однотипные, численность рабочих колеблется незначительно. Есть данные о выпуске продукции за предыдущие 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. После предварительного анализа исходных данных возникло предположение, что суммарный месячный выпуск металлоконструкций существенно зависит от количества уголков в заказах. Проверим это предположение.

Прежде всего, несколько слов об аппроксимации. Мы будем искать закон – аналитическую функцию, то есть функцию, заданную уравнением, которое лучше других описывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а найденное уравнение называется аппроксимирующей функцией для исходной функции, заданной в виде таблицы.

1. Включаем Excel и помещаем на лист таблицу с данными статистики.

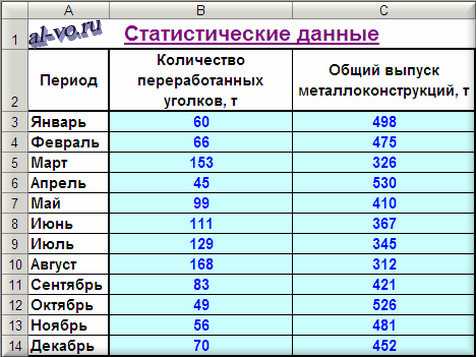
2. Далее строим и форматируем точечную диаграмму, в которой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения исходной функции – общий выпуск металлоконструкций в месяц, заданные таблицей.

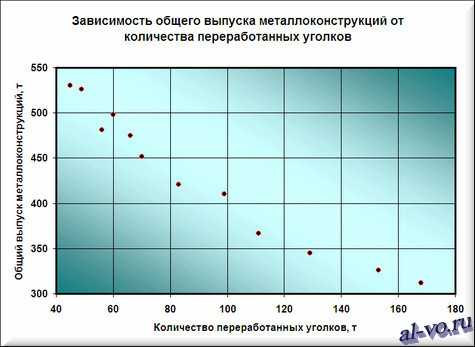
О том, как построить подобную диаграмму, подробно рассказано в статье «Как строить графики в Excel?».

3. «Наводим» мышь на любую из точек на графике и щелчком правой кнопки вызываем контекстное меню (как говорит один мой хороший товарищ — работая в незнакомой программе, когда не знаешь, что делать, чаще щелкай правой кнопкой мыши…). В выпавшем меню выбираем «Добавить линию тренда…».

4. В появившемся окне «Линия тренда» на вкладке «Тип» выбираем «Линейная».

5. Далее на вкладке «Параметры» ставим 2 галочки и нажимаем «ОК».

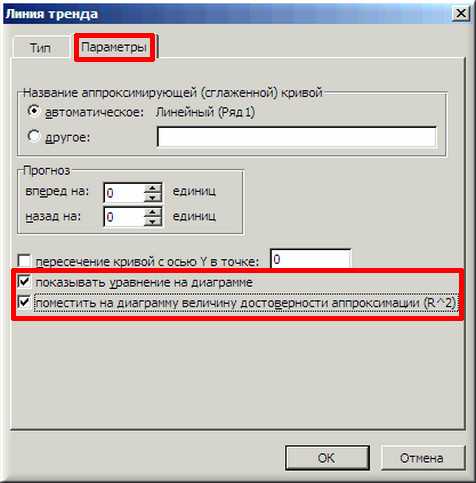
6. На графике появилась прямая линия, аппроксимирующая нашу табличную зависимость.

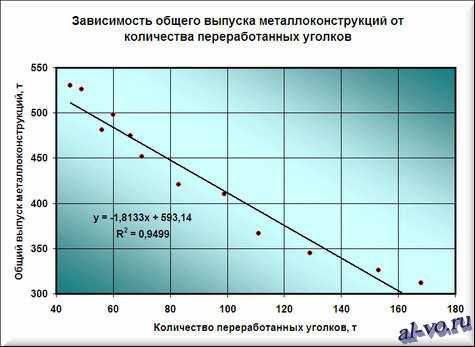
Мы видим кроме самой линии уравнение этой линии и, главное, мы видим значение параметра R 2 – величины достоверности аппроксимации! Чем ближе его значение к 1, тем наиболее точно выбранная функция аппроксимирует табличные данные!

7. Строим линии тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.

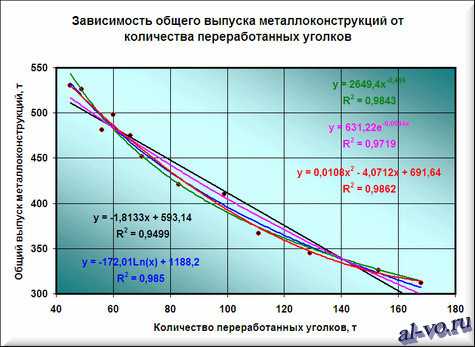
Лучше всех из выбранных функций аппроксимирует наши данные полином второй степени, у него максимальный коэффициент достоверности R 2 .

Однако хочу вас предостеречь! Если вы возьмете полиномы более высоких степеней, то, возможно, получите еще лучшие результаты, но кривые будут иметь замысловатый вид…

Здесь важно понимать, что мы ищем функцию, которая имеет физический смысл

Что это означает? Это означает, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только внутри рассматриваемого диапазона значений X, но и за его пределами, то есть ответит на вопрос: «Какой будет выпуск металлоконструкций при количестве переработанных за месяц уголков меньше 45 и больше 168 тонн!» Поэтому я не рекомендую увлекаться полиномами высоких степеней, да и параболу (полином второй степени) выбирать осторожно!

Итак, нам необходимо выбрать функцию, которая не только хорошо интерполирует табличные данные в пределах диапазона значений X=45…168, но и допускает адекватную экстраполяцию за пределами этого диапазона. Я выбираю в данном случае логарифмическую функцию, хотя можно выбрать и линейную, как наиболее простую. В рассматриваемом примере при выборе линейной аппроксимации в excel ошибки будут больше, чем при выборе логарифмической, но не на много.

8. Удаляем все линии тренда с поля диаграммы, кроме логарифмической функции. Для этого щелкаем правой кнопкой мыши по ненужным линиям и в выпавшем контекстном меню выбираем «Очистить».

9. В завершении добавим к точкам табличных данных планки погрешностей. Для этого правой кнопкой мыши щелкаем на любой из точек на графике и в контекстном меню выбираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.

10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.

Аналогичным образом форматируются любые другие объекты диаграммы в Excel!

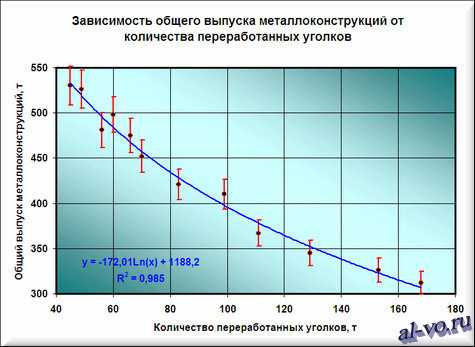
Окончательный результат диаграммы представлен на следующем снимке экрана.

Функция СУММЕСЛИ в Excel

Представляю вашему вниманию третью очень нужную функцию, функция СУММЕСЛИ, как видите, состоит из 2 частей функция СУММ и функция ЕСЛИ то есть логически вы видите что формула будет суммировать определенное значение по определенному критерию. Это особенно актуально, когда нужно выбрать и просуммировать из большого диапазона только определенное значение, например, сколько было списано сырья в производство всего, если вам дали общее списание по предприятию по дням. Вам нужно просто указать, что именно вас интересует и где это взять, а формула сделает всё за вас, ну не все, конечно, саму формулу вы уже сами будете писать.

Функция СУММЕСЛИ в Excel хороша еще тем что, спокойно работает с поименованными диапазонами значений, что значительно упрощает рутинные вычисления. Но стоит помнить, что функция чувствительна к точности написания критериев и даже ошибка в один знак не даст вам правильный результат.

Детальнее о том, как работает СУММЕСЛИ в Excel вы можете ознакомиться и посмотреть видео здесь.

Прогнозирование финансовых результатов методом аппроксимации в Excel

Пример 2. В таблице имеются данные о зарплатах за прошедший год (помесячно). Определить оптимальный способ предсказания размеров зарплат для последующих периодов.

Вид таблицы данных:

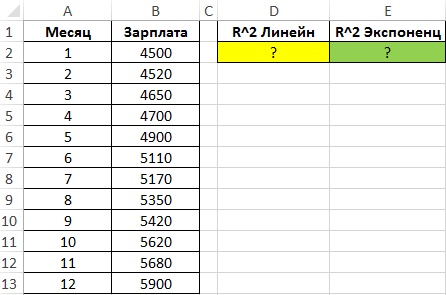
Определим коэффициенты достоверности аппроксимации для линейной и экспоненциальной функций с помощью следующих функций (вводить как формулы массива CTRL+SHIFT+Enter):

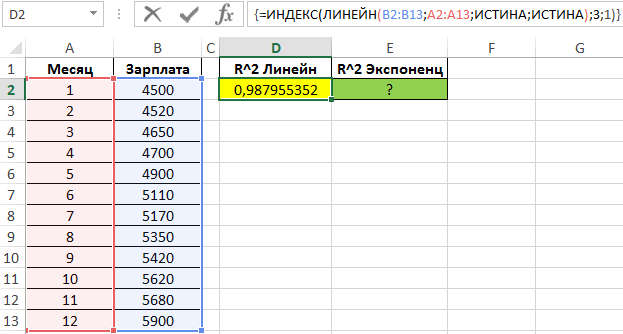
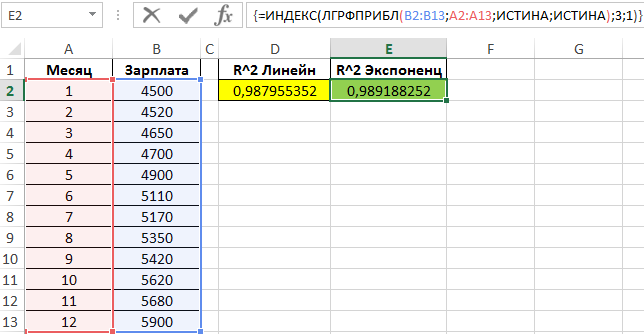
Поскольку обе функции возвращают результат в виде массива данных, в котором в третьей строке первого столбца содержится искомое значение R^2, используем функцию ИНДЕКС для возврата желаемого результата.

Чем ближе значение R^2 к 1, тем выше точность аппроксимации. Как видно, наибольшую точность обеспечивает экспоненциальная функция. Однако разница не является существенной, поэтому использование функции ЛИНЕЙН является допустимым в данном случае.

Итоги.

Результатом всех предыдущих действий стала полученная формула аппроксимирующей функции y=-172,01*ln (x)+1188,2. Зная ее, и количество уголков в месячном наборе работ, можно с высокой степенью вероятности (±4% — смотри планки погрешностей) спрогнозировать общий выпуск металлоконструкций за месяц! Например, если в плане на месяц 140 тонн уголков, то общий выпуск, скорее всего, при прочих равных составит 338±14 тонн.

Для повышения достоверности аппроксимации статистических данных должно быть много. Двенадцать пар значений – это маловато.

Из практики скажу, что хорошим результатом следует считать нахождение аппроксимирующей функции с коэффициентом достоверности R 2 >0,87. Отличный результат – при R 2 >0,94.

На практике бывает трудно выделить один самый главный определяющий фактор (в нашем примере – масса переработанных за месяц уголков), но если постараться, то в каждой конкретной задаче его всегда можно найти! Конечно, общий выпуск продукции за месяц реально зависит от сотни факторов, для учета которых необходимы существенные трудозатраты нормировщиков и других специалистов. Только результат все равно будет приблизительным! Так стоит ли нести затраты, если есть гораздо более дешевое математическое моделирование!

В этой статье я лишь прикоснулся к верхушке айсберга под названием сбор, обработка и практическое использование статистических данных. О том удалось, или нет, мне расшевелить ваш интерес к этой теме, надеюсь узнать из комментариев и рейтинга статьи в поисковиках.

Затронутый вопрос аппроксимации функции одной переменной имеет широкое практическое применение в разных сферах жизни. Но гораздо большее применение имеет решение задачи аппроксимации функции нескольких независимых переменных…. Об этом и не только читайте в следующих статьях на блоге.

Подписывайтесь на анонсы статей в окне, расположенном в конце каждой статьи или в окне вверху страницы.

С интересом прочту Ваши комментарии, уважаемые читатели! Пишите!