Как найти точки пересечения с осями в excel • разложение на множители

Как выстроить точечный график в Excel?

Представим, что у нас имеется таблица с 2-мя рядами данных (затраченное время и количество решенных вопросцев):

В левом столбце представлены данные по времени, которые сотрудники уделяют общению с клиентами, соответственно, в правом — данные по количеству решенных заморочек за уделенное время. Чтоб выстроить точечную диаграмму, выделяем спектр с данными (A1:B10) и на панели вкладок избираем Вставка -> Диаграмма -> Точечная -> Точечная с маркерами:

В итоге получаем обычную диаграмму последующего вида:

Точечный график построен, сейчас настраиваем наружный вид диаграммы под свои предпочтения (добавляем наименования осей, диаграммы, избираем цвета линий и т.д.):

Если нужно выстроить точечную диаграмму с соединением точек линиями, то кроме обычного вида точечного графика также выделяют еще 4 типа точечных диаграмм:

• С маркерами — точки выделяются в виде маркеров;
• С гладкими кривыми и маркерами — диаграмма с соединением точек гладкими кривыми и выделением точек маркерами;
• С гладкими кривыми — диаграмма с соединением точек гладкими кривыми;
• С прямыми отрезками и маркерами — диаграмма с соединением точек прямыми отрезками и выделением точек маркерами;
• С прямыми отрезками — диаграмма с соединением точек прямыми отрезками.

Фортуны для вас и до скорой встречи на страничках блога Tutorexcel.ru!

Как выстроить график в Excel — задачка легкая, но новичков иногда сбивает с толку, какой тип диаграммы избрать либо как верно выстроить таблицу данных.

Итак, Excel дает два типа диаграмм для построения графика —

1. точечную диаграмму — употребляется, когда есть хотя бы два ряда, данные 1-го из их употребляются для определения второго. Пример — обычная функция y=x^2.
2. график — в случае, когда необходимо просто поглядеть как меняется ряд данных.

Точечная диаграмма со стрелками «было-стало»

На тренинге по визуализации недавно один из слушателей озвучил интересную задачу: необходимо наглядно показать изменения затрат и прибыли по определенным товарам в динамике за последние два года. Конечно, можно не напрягаться и пойти по привычному пути, рисуя банальные графики, столбики или даже, прости господи, «тортики». Но если чуть поднапрячься, то неплохим решением в такой ситуации может быть использование особого типа точечной диаграммы со стрелками («было-стало»):

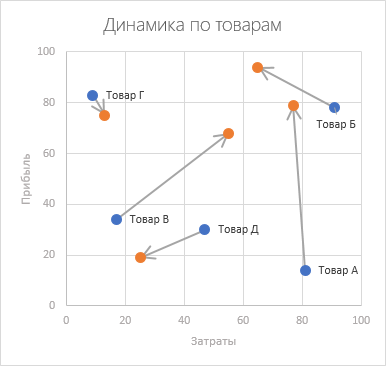
Само-собой, это подходит не только для товаров и затрат-прибыли. С ходу можно придумать много сценариев, где этот тип диаграммы будет «в тему», например:

• Изменение уровня доходов (X) и продолжительности жизни (Y) для разных стран за последние два года.
• Изменение количества клиентов (X) и среднего чека (Y) заказа ресторанов
• Соотношение стоимости компании (X) и количества сотрудников в ней (Y)
• .

Если что-то похожее встречается и в вашей практике, то имеет смысл разобраться, как такую красоту построить.

Про пузырьковые диаграммы (даже анимированные) я уже неоднократно писал. Точечная диаграмма (XY Scatter Chart) — это частный случай пузырьковой (Bubble Chart), но без третьего параметра — размера пузырьков. Т.е. каждая точка на графике описывается всего двумя параметрами: X и Y. Таким образом, построение начинается с подготовки исходных данных в виде двух таблиц:

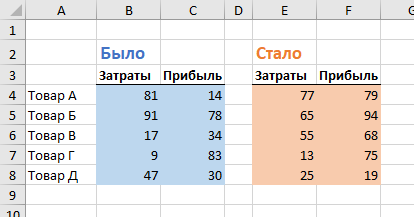
Сначала построим то, что «было». Для этого выделим диапазон A3:C8 и выберем на вкладке Вставка (Insert) команду Рекомендуемые диаграммы (Recommended Charts) , а затем перейдем на вкладку Все диаграммы (All charts) и выберем тип Точечная (XY Scatter Chart) :

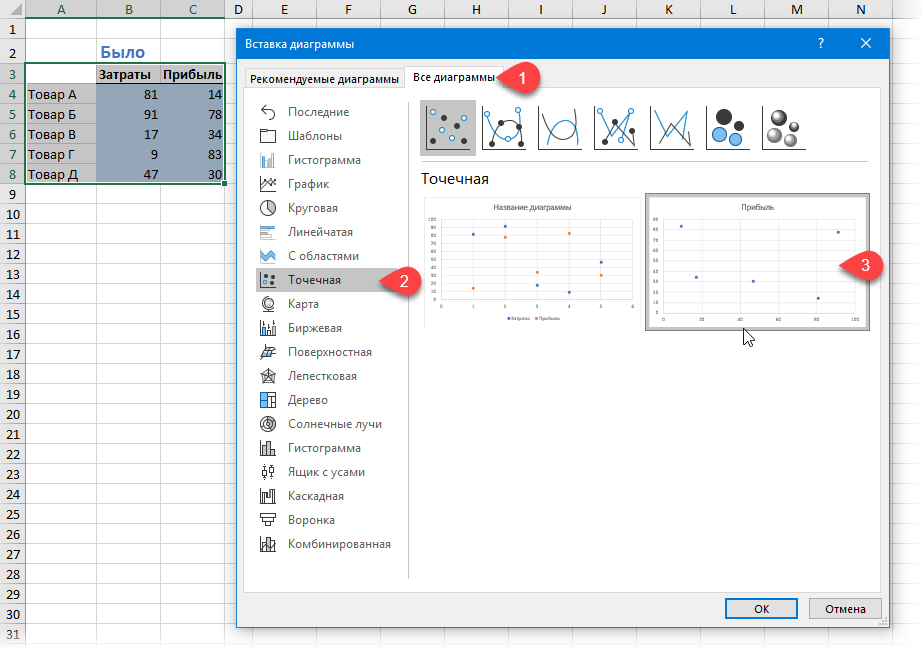
После нажатия на ОК получим заготовку нашей диаграммы.

Теперь добавим на неё данные из второй таблицы «Стало». Проще всего это сделать копированием. Для этого выделим диапазон E3:F8, скопируем его и, выделив диаграмму, выполним в неё специальную вставку через Главная — Вставить — Специальная вставка (Home — Paste — Paste Special) :

В появившемся окне выберем соответствующие опции вставки:

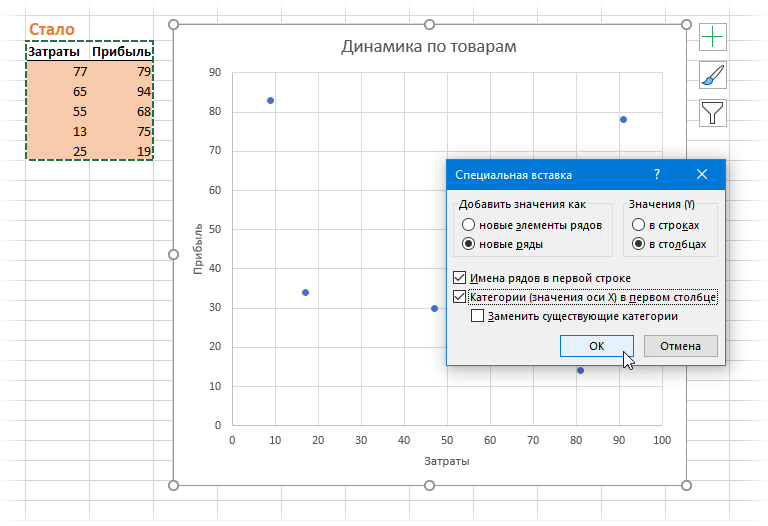
После нажатия на ОК на нашей диаграмме появится второй комплект точек («стало»):

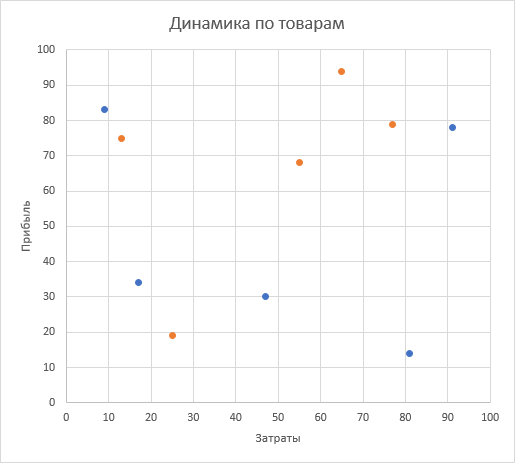
Теперь самое интересное. Для имитации стрелок нужно будет из данных первой и второй таблиц подготовить третью таблицу вот такого вида:

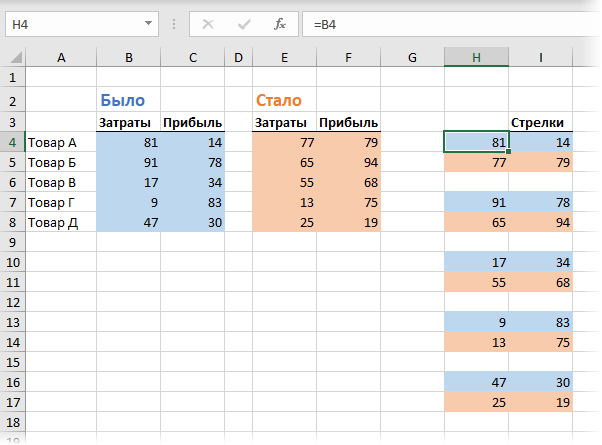
Обратите внимание как она устроена:

• строки из исходных таблиц попарно чередуются, фиксируя начало и конец каждой стрелки
• каждая пара отделена от других пустой строкой, чтобы на выходе получились отдельные стрелки, а не одна большая
• если данные могут изменяться в будущем, то имеет смысл использовать не числа, а ссылки на исходные таблицы, т.е. в ячейке H4 ввести формулу =B4, в ячейку H5 ввести формулу =E4 и т.д.

Выделим созданную таблицу, скопируем ее в буфер и добавим к нашей диаграмме при помощи специальной вставки, как это уже делали ранее:

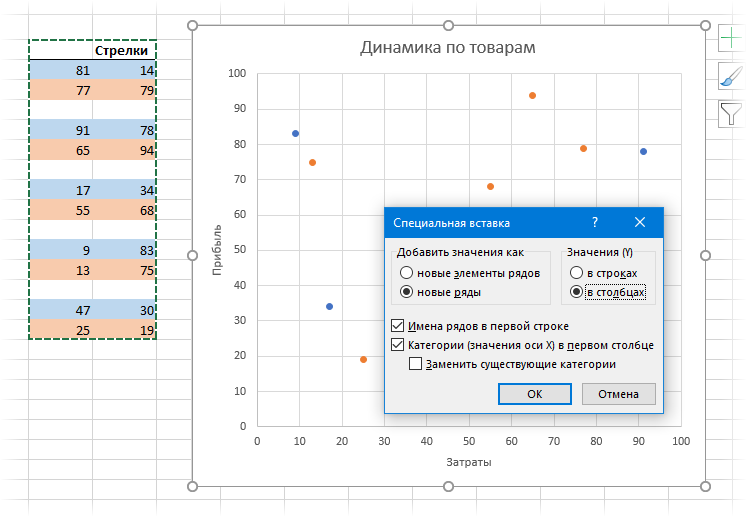
После нажатия на ОК на диаграмме появятся новые точки начала и конца каждой стрелки (у меня они серого цвета), закрывающие уже построенные синие и оранжевые. Щелкнем по ним правой кнопкой мыши и выберем команду Изменить тип диаграммы для ряда (Change Series Chart Type) . В открывшемся окне для исходных рядов «было» и «стало» оставим тип Точечная, а для ряда «стрелок» зададим Точечная с прямыми отрезками:

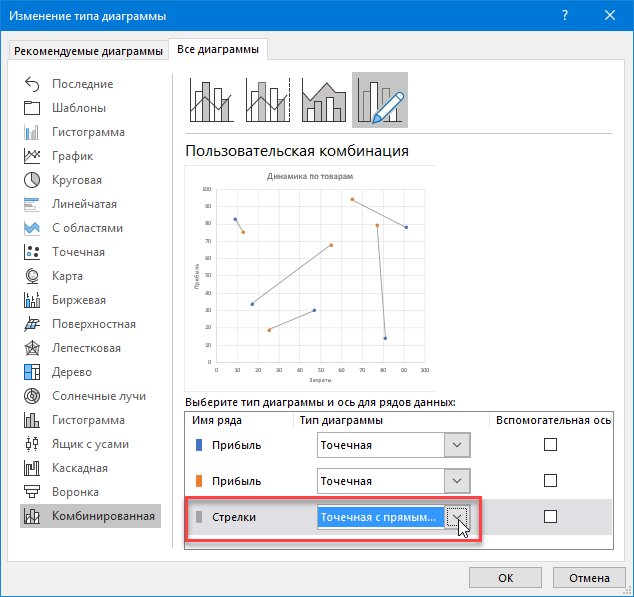
После нажатия на ОК наши точки «было» и «стало» будут соединены прямыми отрезками. Останется щелкнуть по ним правой кнопкой мыши и выбрать команду Формат ряда данных (Format Data Series) , а затем настроить параметры линий: толщину, тип стрелки и их размеры:

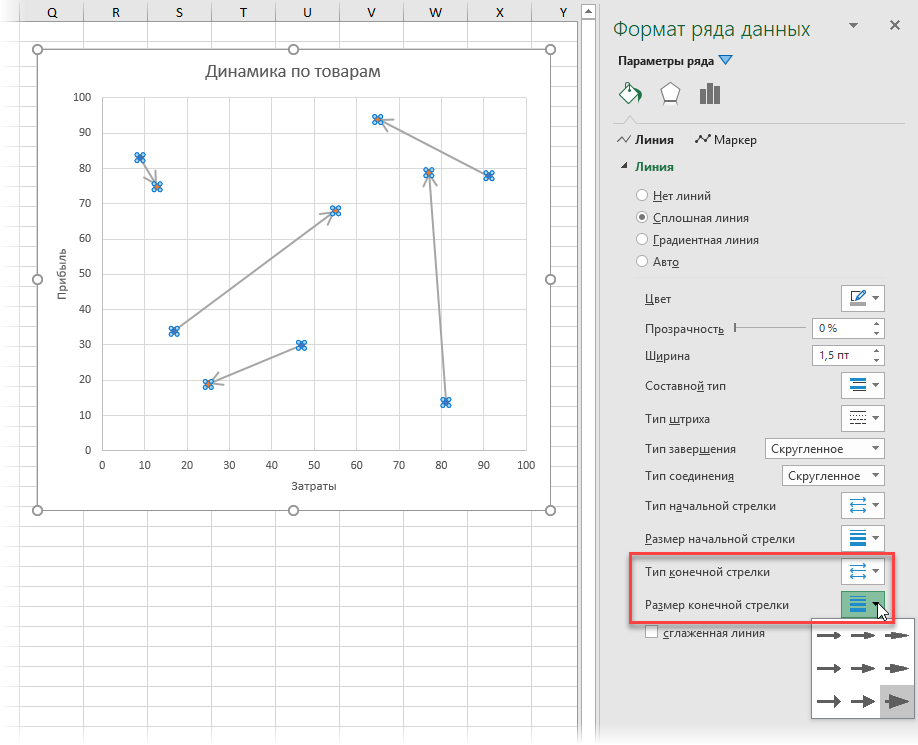
Для наглядности ещё неплохо бы добавить названия товаров. Для этого:

1. Щелкните по любой точке и выберите в контекстном меню Добавить подписи данных (Add Data Labels) — добавятся числовые подписи точек
2. Щелкните по подписям правой и выберите команду Формат подписей (Format Labels)
3. В открывшейся панели включите флажок Значения из ячеек (Values from cells) , нажмите кнопку Выбрать диапазон и выделите названия товаров (A4:A8).

Редактирование графика

Если вы хотите изменить размещение графика, то дважды кликаем по графику, и в « КОНСТРУКТОРЕ » выбираем « Переместить диаграмму ».

Как построить график в Excel – Переместить диаграмму

В открывшемся диалоговом окне выбираем, где хотим разместить наш график.

Как построить график в Excel – Перемещение диаграммы

Мы можем разместить наш график на отдельном листе с указанным в поле названием, для этого выбираем пункт « на отдельном листе ».

В случае если необходимо перенести график на другой лист, то выбираем пункт « на имеющемся листе », и указываем лист, на который нужно переместить наш график.

Разместим график по данным таблицы на отдельном листе с названием « Курс доллара, 2016 год ».

Как построить график в Excel – Перемещение графика на отдельный лист

Теперь книга Excel содержит лист с графиком, который выглядит следующим образом:

Как построить график в Excel – График курса доллара на отдельном листе

Поработаем с оформлением графика. С помощью Excel можно мгновенно, практически в один клик изменить внешний вид диаграммы, и добиться эффектного профессионального оформления.

Во вкладке « Конструктор » в группе « Стили диаграмм » находится коллекция стилей, которые можно применить к текущему графику.

Как построить график в Excel – Стили диаграмм

Для того чтобы применить понравившийся вам стиль достаточно просто щелкнуть по нему мышкой.

Как построить график в Excel – Коллекция стилей диаграмм

Теперь наш график полностью видоизменился.

Как построить график в Excel – График с оформлением

При необходимости можно дополнительно настроить желаемый стиль, изменив формат отдельных элементов диаграммы.

Ну вот и все. Теперь вы знаете, как построить график в Excel, как построить график функции, а также как поработать с внешним видом получившихся графиков. Если вам необходимо сделать диаграмму в Excel, то в этом вам поможет эта статья.

Решение

Шаг 1

Для начала обратим внимание, что исходный тип диаграммы — График с маркерами

Ряды этого типа описываются так:

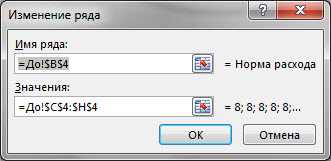
Заметьте, что тут нет значений координат по оси X, а есть только координаты по условной оси Y. Этим подразумевается, что условная ось X — общая для всех рядов, а также, что при их построении не используются значения, отличные от заранее фиксированного ряда оси X. Вот есть у нас периоды: 1, 2, 3 и т.д., нанесенные на ось Х, и использовать можно только их. Периода, где X=3.5 не существует для данного типа диаграммы.

Однако, нам для решения этой задачи необходимо, чтобы мы могли задавать любое значение X, в том числе промежуточные, так как наши линии как раз пересекаются где-то «между периодами». Поэтому тип диаграммы мы меняем для всех рядов с «графика с маркерами» на «точечную с прямыми отрезками и маркерами».

Следует упомянуть, что наш случай осложняется наличием двух вертикальных осей: основной и вспомогательной, так как значения расхода материала и объёма производства сильно друг от друга отличаются.

Шаг 2

Теперь нам необходимо нанести на диаграмму дополнительные ряды данных:

1. Точки пересечения линий расхода материала с нормами расхода. Таких точек у нас будет 3, исходя из условий примера. Эти точки нам необходимо будет расчитать, вспомнив школьный курс геометрии (см. лист Треугольники). В файле учебного примера на листе После в таблице N3:Q5 мы получили координаты нужных точек путем нехитрых формул. Тип диаграммы Точечная в отличие от рядов с показателями работы производства.

2. Точки пересечения найденных значений по оси X с объемом производства. Расчитывается в таблице N8:Q10 по близким формулам. Тип диаграммы Точечная.

3. Пунктирные линии, которые мы рисуем из эстетических соображений. Таблица с их координатами находится в N12:P18.

Добавляем ряды данных в соответствии с теми точками, которые мы расчитали. Щёлкните ПКМ по диаграмме и выберите «Выбрать данные…», далее воспользуйтесь кнопкой «Добавить».

Пример одного из рядов:

Шаг 3

Отформатируйте линии и маркеры новых рядов данных, так как вам необходимо. Готово!

Изучим способы поиска точек пересечения двух графиков и графика с осью координат, а также варианты их отображения в Excel.

Поиск точек пересечения графиков может применяться, к примеру, при графическом способе решения различных уравнений в математике или при поиске точки безубыточности предприятия в бизнесе. Если графики заданы какими-либо алгебраическими функциями, то точное решение оптимальнее искать математически, приравняв функции друг к другу. В данной статье мы разберем как найти точки пересечения для линейного графика, в котором линии имеют одинаковые координаты по оси абсцисс (горизонтальная) и различные координаты по оси ординат (вертикальная).

Как мы помним из школьного курса математики, через две любые несовпадающие точки можно провести прямую и только одну. Поэтому зная их координаты мы можем составить уравнение прямой. Таким образом решая систему уравнений, состоящую из уравнений двух прямых, мы можем найти место пересечения:

Общий принцип поиска координат следующий: для каждых двух соседних пар точек на оси абсцисс (на рисунке x1 и x2 расположены по горизонтали) проверяется условие пересекаются ли линии, то есть выполняется ли условие y1 ≥ z1 и y2 ≤ z2, или наоборот y1 ≤ z1 и y2 ≥ z2 (на рисунке y1, y2, z1 и z2 расположены по вертикали).

Методы решения

Для нахождения точек пересечения с осями координат можно использовать различные методы. Рассмотрим наиболее простые из них.

1. Графический метод

Для применения данного метода необходимо построить график функции на координатной плоскости и визуально определить, где он пересекает оси координат. Этот метод подходит для функций, которые можно построить и рассмотреть на графике.

2. Аналитический метод

Для аналитического нахождения точек пересечения с осями координат необходимо приравнять соответствующую координату функции к нулю и решить полученное уравнение. Если при решении получится несколько корней, то это будут искомые точки пересечения с осями координат.

3. Использование таблиц и графиков функций

Для сложных функций, где нахождение точек пересечения с осями координат методами графика или аналитически невозможно, можно использовать таблицы значений функции и построение графиков функций на компьютере. В таблице нужно выбирать значения аргумента, затем находить соответствующие значения функции и выявлять в каких местах они равны нулю. Затем на графике можно убедиться, что найденные точки являются точками пересечения с осями координат.

Таким образом, выбор метода нахождения точек пересечения с осями координат будет зависеть от сложности функции и доступных инструментов для ее решения.

Как в Excel построить точечную диаграмму

Диаграммы этого типа используют для выявления потенциальных связей между двумя переменными. Например, размышляя о качестве, вы, наверное, собираете данные, которые позволяют сравнить время, необходимое для производства той или иной детали, с количеством дефектов, обнаруженных в этих деталях. Точеные диаграммы отображают эти данные в графическом виде. Пользуясь определенными методами интерпретации, вы выявляете наличие корреляции между двумя указанными переменными.

На рис. 1 представлена точечная диаграмма, сравнивающая продолжительность временных интервалов, затраченных на производство, с частотой возникновения дефектов. Из этой диаграммы следует, что чем продолжительнее время производства, тем меньше количество дефектов.

Рис. 1. Точечная диаграмма

Диаграммы точечного типа достаточно просто создавать в программе Excel. Сначала выделите ячейки диапазона В2-С9 (рис. 2) и щелкните на кнопке X,Y (Scatter) (Точечная) вкладки Insert (Вставка). Затем щелкните на значке, который расположен в верхнем левом углу появившегося меню.

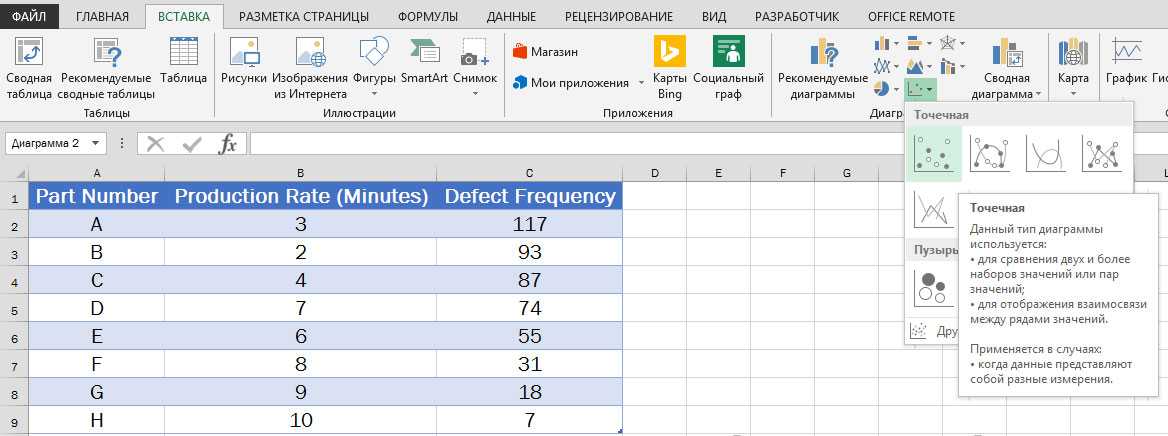
Рис. 2. Создание точечной диаграммы

Присвойте этой диаграмме, а также горизонтальной и вертикальной осям названия, как мы это делали в примере с диаграммой Парето.

Если вы хотите распечатать только точечную диаграмму, выберите ее щелчком мыши. Затем в меню кнопки Файл выберите команду Print → Quick Print (Печатать → Быстрая печать) (рис. 3). Для того чтобы убедиться в том, что на печатающее устройство будет отправлено именно то, что вам требуется, выберите в меню кнопки Файл команду Print → Print Preview (Предварительный просмотр). Как альтернативный вариант нажмите комбинацию клавиш Ctrl+P (что обозначает Print), предварительно выбрав нужную вам диаграмму щелчком мыши.

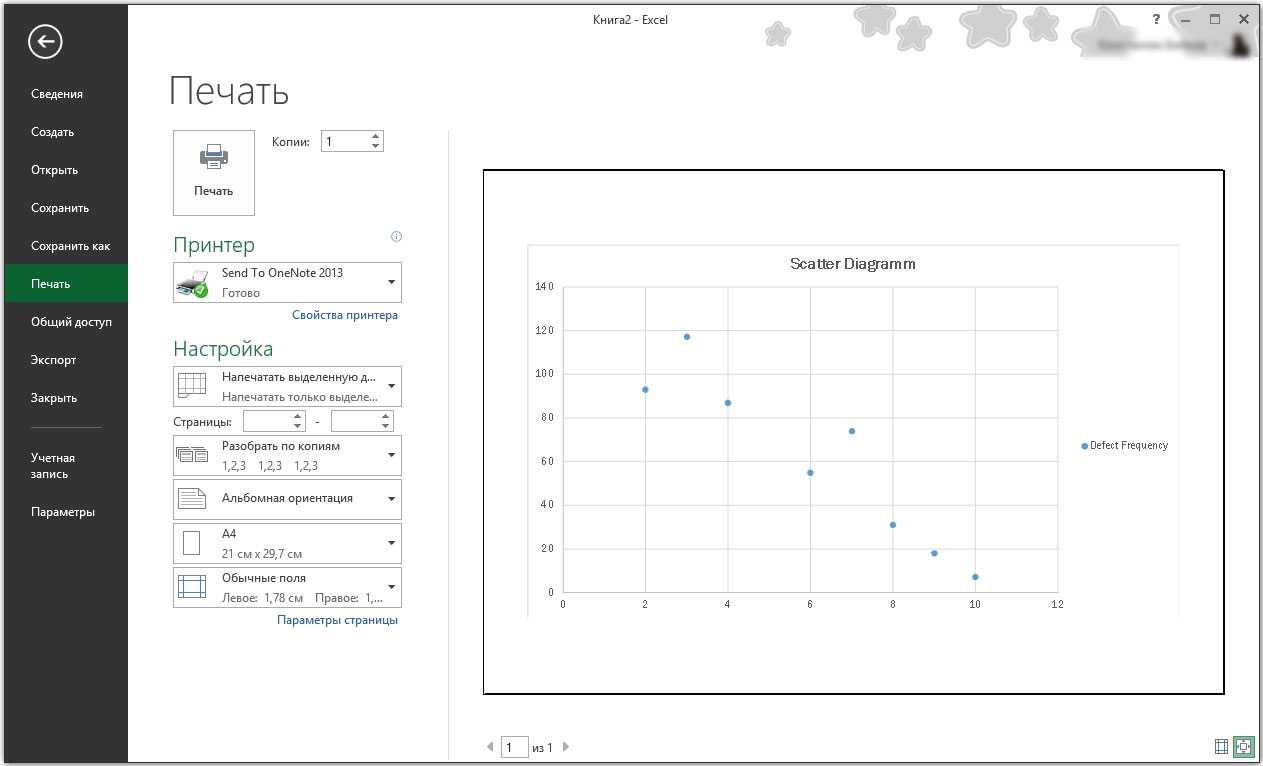
Рис. 3. Команды для печати данных и диаграмм расположены в подменю Print (Печать)

Точки пересечения графиков в Excel

Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.

Строим графики с точками пересечений

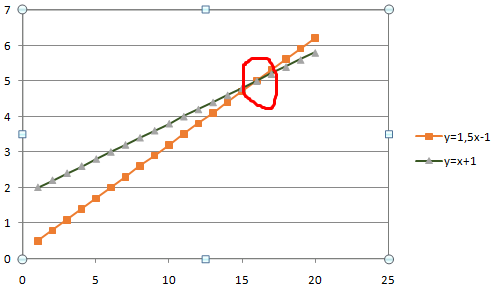
Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.

Находим точку пересечения графиков в Excel

В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.

Первый способ. Найти общие значения в рядах данных для указанных функций.

В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.

Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.

Изменим график, добавив новые данные. Получим две пересекающиеся линии.

Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».

Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.

Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.

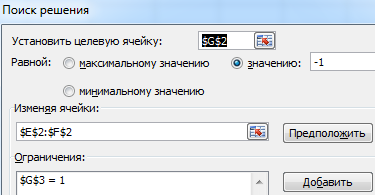
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.

Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.

Точки пересечения для трех показателей

Существует три показателя, которые измерялись во времени.

По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).

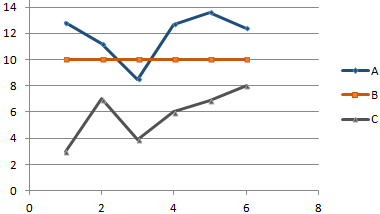
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.

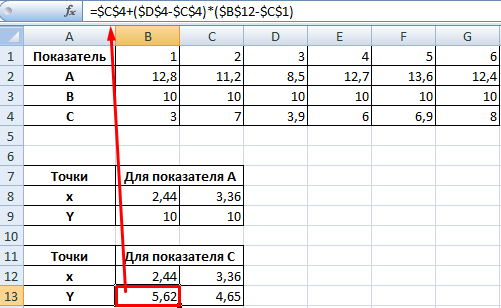
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:

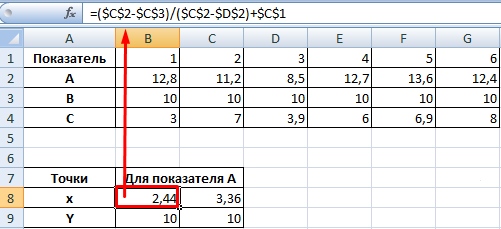
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.

Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:

На основе новых данных построим точечные диаграммы на том же поле (где наши графики).

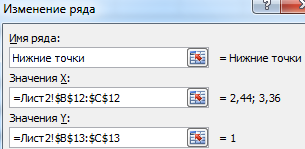
Получается такой рисунок:

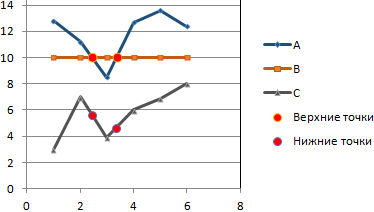
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:

Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.

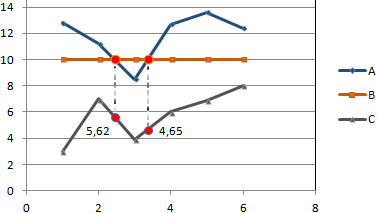
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.

Общие сведения

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.

Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.

Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.

Классификация уравнений

Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:

1. Линейные.
2. Квадратные.
3. Кубические.
4. Биквадратные.

Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S – коэффициенты при переменных, а U – константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).

Равносильные тождества

При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.

Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II – III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 {R(t)=0 и S(t)=0}.

Математические преобразования

Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:

1. Правильное раскрытие скобок с учетом алгебраической операции и знаков.
2. Упрощение выражения (приведение подобных величин).
3. Перенос элементов в любые части равенства с противоположным знаком.
4. Возможность прибавлять или вычитать эквивалентные величины.
5. Деление и умножение на любые эквивалентные значения, не превращающие тождества в пустое множество.

Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.

Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.

Разложение на множители

Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:

1. Квадрат суммы и разности: (p+r)^2=p^2+2pr+r^2 и (p-r)^2=p^2-2pr+r^2 соответственно.
2. Разность квадратов: p^2-r^2=(p-r)(p+r).

В некоторых случаях можно воспользоваться сразу двумя соотношениями, т. е. выделить квадрат суммы, а затем из первого — разность квадратов. Выделение первого осуществляется группировкой посредством скобок в выражении, а затем введение положительного и отрицательного элементов, т. е. s^2+4s-5=s^2+4s+4-4-5=(s^2+4s+4)-4-5=(s+2)^2 -9. Для получения всех элементов формулы “p+r)^2=p^2+2pr+r^2” нужно прибавить, а затем отнять 4. При этом значение равенства не изменится, поскольку 4-4=0.

Следует отметить, что математические преобразования выражения (s+2)^2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.

Путем составления системы уравнений

Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:

Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.

Порядок действий при решении системы уравнений можно рассмотреть на примере:

Решение будет иметь следующий вид:

Данные уравнения являются линейными, поэтому график каждого из них представляет собой прямую. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и является решением системы уравнений.

Решение системы представляет сбой единственную пару чисел:

Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).

В процессе решения линейной системы можно столкнуться с разными ситуациями:

• система обладает единственным решением, прямые пересекаются;
• решения системы отсутствуют. прямые параллельны;
• система обладает бесчисленным множеством решений, прямые совпадают.

При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.

В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:

Решение имеет следующий вид:

График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:

Центр окружности в точке О(0; 0), радиус равен 1.

Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).

Ответ: (0; 1); (-1; 0).

Можно решить систему графическим способом:

В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).

Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).

В качестве еще одного примера можно решить следующую систему:

Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.

Далее необходимо построить график функции:

График будет являться ломанной:

Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:

При помещении обоих графиков в одну систему координат получится следующая ситуация:

Таким образом, получились три точки пересечения: А(1; 0), т. В(-1; 0), т. С(0; -1)

Построение графиков в Excel по данным таблицы

В MS Excel есть возможность не только проводить вычисления, используя разные формулы, но и также строить на их основе различные диаграммы: гистограммы, круговые диаграммы, точечные и т.д.В этом уроке мы разберем, для чего применяют графики.И так, графики – это разновидность диаграммы, схожая с гистограммой. Они бывают трех видов: простой, график с накоплением и нормированный график с накоплением. Каждый из этих графиков бывает двух видов: с маркером и без. Так эти два вида строятся одинаково, рассмотрим только маркированные графики.Коротко опишем применение каждого графика, и далее на примерах разберем более подробно, как их построить.a) Простой график нужен для того, чтобы изобразить, как изменяется некое значение во времени (прибыль по месяцам; рождаемость по годам и т.д.).b) График с накоплением показывает, как изменяется составляющая целого значения с течением времени. (Лучше использовать диаграмму с накоплением)c) Нормированный график с накоплением показывает изменение доли каждого значения с течением времени.Есть еще объемный график, который схож с простым графиком. Поэтому мы покажем только его конечный вид.