Как построить производную по графику в программе excel

Метод приращений

Метод приращений является частным случаем метода хорд, когда полюсное расстояние принимается равным выделенным участкам на оси абсцисс (при этом все участки должны иметь одинаковую величину H=Δt ). В этом случае приращение перемещений на выделенном участке представляет собой среднюю скорость на данном участке в некотором масштабе

Аналогично дифференцируется диаграмма скоростей для получения диаграммы ускорений. Метод удобен тем, что не надо проводить никаких вспомогательных линий, дифференцирование осуществляется очень быстро. Однако при повторном дифференцировании (дифференцировании диаграммы скоростей для получения диаграммы ускорений) приращения уменьшаются и точность результатов резко снижается (получается большая относительная погрешность).

При анализе и, особенно, при синтезе механизмов может быть графически задана функция изменения скорости звена, а необходимо иметь функцию перемещения (или необходимо определить функцию изменения скорости при заданной графически функции ускорения). В этом случае можно воспользоваться методами графического интегрирования.

Применяется два метода графического интегрирования – метод площадей и метод хорд.

Производная по графику в Excel: основы и принципы

Для построения производной по графику в Excel необходимо иметь график функции, для которой вы хотите найти производную. График должен быть построен на основе данных или формулы.

Когда у вас есть график функции, вы можете использовать функцию , чтобы получить приближенное значение производной в каждой точке графика.

Чтобы построить график производной, вам нужно:

1. Выберите диапазон ячеек, где вы хотите построить график производной.
2. Вводите формулу в ячейке верхнего левого угла диапазона, затем нажмите Enter.
3. Выделите диапазон ячеек, в которые была введена формула , затем перетащите их к последней ячейке в диапазоне, чтобы скопировать формулу в каждую ячейку.

После выполнения этих шагов вам будет построен график производной функции. Чтобы визуализировать график, вы можете использовать дополнительные инструменты Excel, такие как установка различных стилей линий, изменение цвета и толщины линий, добавление подписей осей и т.д.

Важно отметить, что полученная производная будет являться приближенной, поскольку она будет основана на данных графика функции. Чтобы получить более точное значение производной, необходимо увеличить плотность точек на графике функции или использовать другие методы, такие как численное дифференцирование

Теперь вы знаете основы и принципы построения производной по графику в Excel. Не стесняйтесь экспериментировать и использовать другие функции Excel для улучшения ваших графиков и анализа данных.

Как делать производные в Excel

Microsoft Excel не имеет возможности генерировать производное уравнение по заданной формуле, но вы все равно можете использовать программу для вычисления значений как для формулы, так и для ее производной и построения их на графике. Это позволяет сравнивать формулу с ее производной, даже если вы не знаете самой производной. Поскольку Excel берет на себя все вычисления, вы можете использовать этот метод, даже если вы не знаете исчисления.

Введите нижнюю границу горизонтального диапазона, который вы хотите построить, в ячейке A1. Например, чтобы построить график от -2 до 2, введите «-2» в A1 (опуская кавычки здесь и на всех этапах).

Введите расстояние между точками графика в ячейку D1. Чем меньше расстояние, тем точнее будет выглядеть ваш график, но использование слишком большого количества точек может замедлить обработку. Для этого примера введите «0,1», что даст 41 точку графика из -2 и 2. Если вы используете меньший или больший диапазон, измените расстояние соответственно, чтобы получить как минимум несколько десятков точек, но не более нескольких тысяч. .

Введите формулу «= A1 + $ D $ 1» в ячейку A2. Перетащите маркер заполнения в углу ячейки вниз, чтобы повторить формулу для такого количества точек, которое необходимо для достижения желаемого верхнего диапазона.

Поместите исходную формулу в ячейку B1, начиная со знака равенства и заменив переменную на «A1». Например, чтобы использовать уравнение «y = 2x ^ 2», введите «= 2 * A1 ^ 2»

Обратите внимание, что Excel не умножает смежные члены автоматически, поэтому для умножения необходимо ввести звездочку

Дважды щелкните маркер заполнения в ячейке B1, чтобы заполнить все необходимые ячейки в столбце B.

Введите «= (B2-B1) / $ D $ 1» в ячейку C1. Это уравнение находит производную для вашей формулы в каждой точке, используя определение производной «dy / dx»: разница между каждой строкой в ​​столбце B составляет «dy», а значение, которое вы выбрали для D1, представляет «dx». Дважды щелкните маркер заполнения в C1, чтобы заполнить столбец.

Прокрутите вниз и удалите последнее число в столбце C, чтобы избежать неточного значения для последней производной.

Щелкните и перетащите от заголовка столбца A к заголовку C, чтобы выделить первые три столбца. Откройте вкладку «Вставка» на ленте и нажмите «Диаграммы», «Точечная диаграмма», а затем «Точечная диаграмма с плавными линиями» или другой тип диаграммы разброса, если необходимо. Excel отобразит исходную формулу как «Серия 1», а производную — как «Серия 2».

Что такое производная функции и зачем она нужна в Excel?

В Excel производная функции может быть полезной во многих случаях

Во-первых, она позволяет определить максимальное или минимальное значение функции, что может быть важно при поиске оптимальных решений или при анализе данных. Например, если у вас есть функция, которая описывает зависимость прибыли от количества произведенных товаров, вы можете использовать производную, чтобы найти точку, где прибыль будет наибольшей

Во-вторых, производную функции можно использовать для анализа трендов и изменений в данных. Если у вас есть временные ряды или данные, которые меняются во времени, вы можете посчитать производную и посмотреть, как она изменяется. Это может дать вам информацию о темпе роста или спада показателей.

Кроме того, производная функции может быть полезна при решении математических задач, таких как нахождение экстремумов (точек максимума или минимума) или построение графиков функций. Excel предоставляет удобные инструменты для вычисления производных и визуализации результатов.

Однако стоит отметить, что для некоторых функций производная может быть сложной или даже невозможной для вычисления аналитически. В таких случаях можно использовать численное дифференцирование или приближенные методы расчета производной.

Построение производной по графику в Excel: пошаговое руководство

Шаг 1: Введите данные функции

Перед тем как построить график функции, необходимо ввести данные. Введите значения функции в столбец A и соответствующие значения аргумента в столбец B. Например, если функция f(x) = x^2 — 3x + 2, введите значения функции в столбец A и значения аргумента в столбец B.

Функция	Аргумент
1
2	1
2	2
1	3
-2	4

Шаг 2: Построение графика функции

Для построения графика функции выберите столбец A и B, затем перейдите во вкладку «Вставка» и выберите тип графика, который вам нужен. В данном случае рекомендуется использовать график «Рассеяние» для точечной диаграммы.

Шаг 3: Вычисление производной

Чтобы построить производную по графику функции, необходимо вычислить значение производной в каждой точке. Для этого вычислите изменение функции (разность между двумя соседними точками) и разделите его на изменение аргумента (разность между соответствующими значениями аргумента).

Например, для вычисления производной функции f(x) = x^2 — 3x + 2 в точке x = 2, используйте следующую формулу:

Производная = (f(x + h) — f(x)) / h, где h — малое значение приращения аргумента

Заменив значения функции и аргумента в формулу, получим:

Производная = (f(2 + h) — f(2)) / h = ((2 + h)^2 — 3(2 + h) + 2 — (2^2 — 3 * 2 + 2)) / h

Шаг 4: Построение графика производной

Чтобы построить график производной, выберите столбцы с значениями аргумента и производной. Затем, аналогично построению графика функции, выберите тип графика «Рассеяние».

Вычисление производной по графику функции в Excel может быть полезным инструментом для анализа и визуализации данных. Следуя этому пошаговому руководству, вы сможете построить производную по графику функции и использовать ее для дальнейшего анализа и исследования данных.

Однако…

Увы, не стоит думать, что на практике легко получить необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!

Дело в том, что измерения прогибов требуется выполнять с точностью ~1 мкм и стараться максимально уменьшать шаг замеров h, «устремляя его к нулю», хотя и это может не помочь избежать ошибок.

Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.

Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$…

Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.

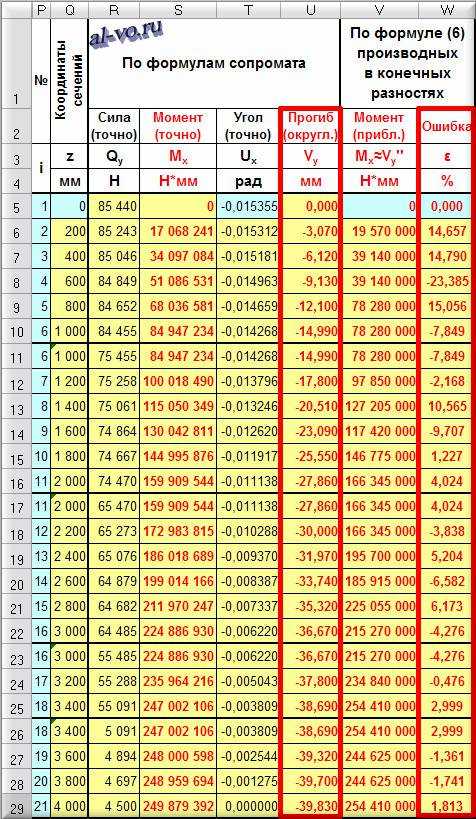
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i=4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении (ε₂₁=1,813%).

Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — аппроксимировать замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.

Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.

Вычисление производной численными методами всегда необходимо выполнять очень осторожно!

Другие статьи автора блога

На главную

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

1. Коэффициент (a) можно найти с помощью следующих фактов:

   – Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

   – Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

   – Аналогично с (a<-1), только график вытянут вниз.

   – Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

   – Аналогично (a∈(-1;0)), только ветви направлены вниз.

2. Парабола пересекает ось y в точке (c).

3. (b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) – абсциссы (икса) вершины параболы:

   (x_в=-frac{b}{2a}) (b=-x_вcdot 2a)

Пример (ЕГЭ):

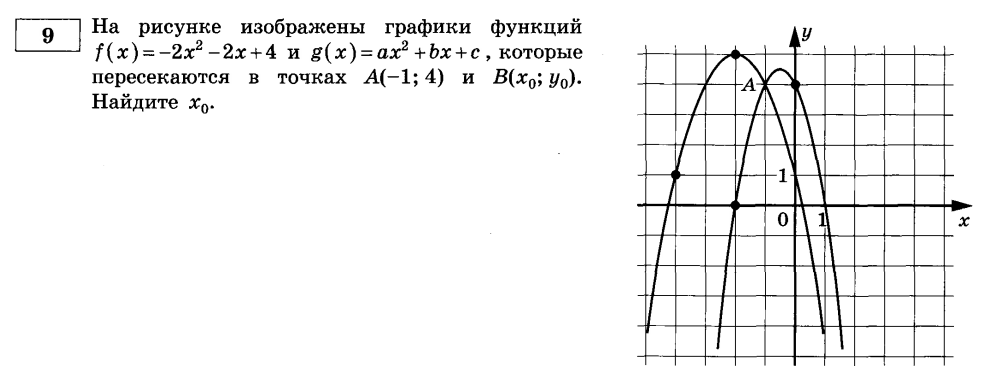
Решение: Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

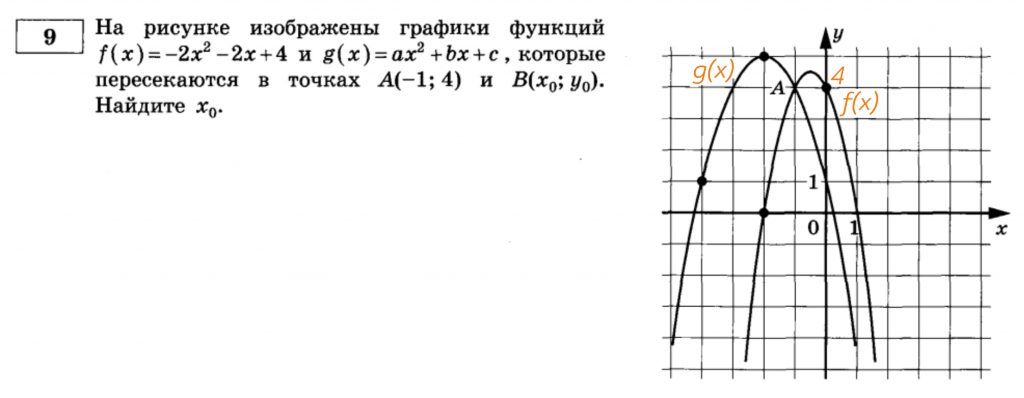
Значит нужно найти коэффициенты у параболы, которая лежит повыше. Коэффициент (c) у неё равен (1). Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

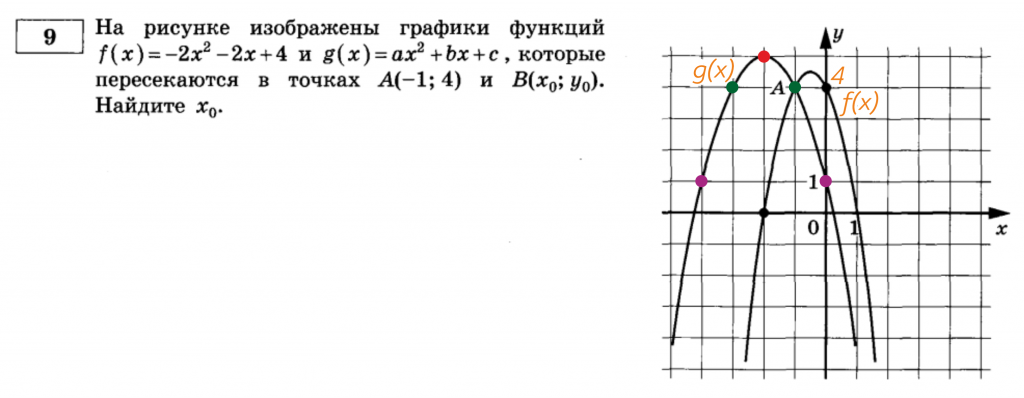
Найдем (b). (x_в=-2), (a=-1).

(x_в=-frac{b}{2a}) (-2=-frac{b}{-2}) (b=-4)

Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:

(-x^2-4x+1=-2x^2-2x+4) (-x^2-4x+1+2x^2+2x-4=0) (x^2-2x-3=0) (D=4+4cdot 3=16=4^2) (x_1=frac{2-4}{2}=-1);    (x_2=frac{2+4}{2}=3).

Ответ: (3).

Использование трендлайна

В Excel можно легко создать трендлайн, который будет проходить через данные на графике и представлять их общую тенденцию.

Чтобы добавить трендлайн в Excel, нужно выделить данные на графике, для которых вы хотите создать трендлайн. Затем выберите «Добавить элемент графика» и «Трендлайн» во всплывающем меню.

В диалоговом окне «Трендлайн» появится список доступных типов трендлайнов. Вы можете выбрать определенный тип трендлайна, который наилучшим образом подходит для ваших данных.

После выбора типа трендлайна нажмите кнопку «OK», и Excel автоматически добавит трендлайн на график.

Примечание: Обратите внимание, что трендлайн — это приближение и может не всегда идеально соответствовать данным на графике. Однако это полезный инструмент для определения общей функции, представленной на графике

Теперь у вас есть возможность использовать трендлайн для определения функции по графику в Excel. Это может быть особенно полезно, если вы хотите аппроксимировать данные и использовать их для прогнозирования будущих значений.

Метод дифференцирования по формуле

Метод дифференцирования по формуле является одним из наиболее распространенных способов вычисления производной в программе Excel. Он основан на использовании аналитических формул для вычисления производной функции.

Для применения метода дифференцирования по формуле в Excel необходимо знать аналитическую формулу для производной функции, которую необходимо вычислить. Например, если нужно вычислить производную функции y = x^2, то аналитическая формула для этой функции будет y’ = 2x.

При использовании метода дифференцирования по формуле в Excel необходимо в ячейку ввести аналитическую формулу для производной функции, а затем с помощью функции применить эту формулу к данным. Например, если нужно вычислить производную функции y = x^2 в точке x = 2, то можно воспользоваться следующей формулой: =2*A1, где A1 — ячейка, содержащая значение x, равное 2.

Однако при использовании метода дифференцирования по формуле в Excel нужно учитывать, что это не всегда удобный способ вычисления производной, особенно если функция имеет сложную аналитическую формулу. В таких случаях может быть проще воспользоваться другими методами вычисления производной, например, численными методами.

Вывод: метод дифференцирования по формуле является эффективным способом вычисления производной в Excel, если у вас есть аналитическая формула для производной функции. Однако, если формула сложная или требуется вычисление производной в нескольких точках, может быть удобнее воспользоваться другими методами вычисления производной.

Однако…

Увы, не стоит думать, что на практике легко получить
необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!

Дело в том, что измерения прогибов требуется выполнять с точностью ~1 мкм и стараться максимально уменьшать шаг замеров h

, «устремляя его к нулю», хотя и это может не помочь избежать ошибок.

Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.

Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$…

Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.

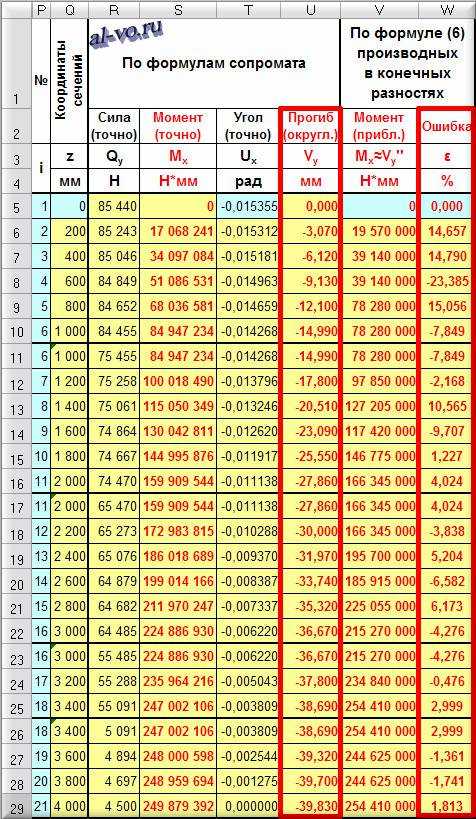
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i

=4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении (ε 21

=1,813%).

Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.

Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.

Вычисление производной численными методами всегда необходимо выполнять очень осторожно!

Уважаемые читатели, отзывы и комментарии к статье, размещайте в специальном блоке ниже статьи.

Чтобы получать информацию о выходе новых статей на блоге, подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи.

Прошу

УВАЖАЮЩИХ


труд автора скачать файл с примером

ПОСЛЕ ПОДПИСКИ


на анонсы статей.

Графическое дифференцирование начинают с построения графика функции по заданным значениям. При экспериментальном исследовании такой график получают с помощью самопишущих приборов. Далее проводят касательные к кривой в фиксированных положениях и вычисляют значения производной по тангенсу угла, образованного касательной с осью абсцисс.

На рис. 5.8, а
изображена кривая полученная экспериментально на установке (рис. 5.6). Определение углового ускорения (искомой функции) проводят графическим дифференцированием по соотношению:

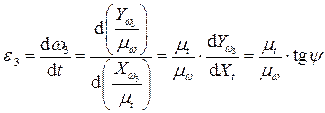(5.19)

Тангенс угла наклона касательной к кривой в некоторой точке i

представляют в виде отношения отрезков , где К
– выбранный отрезок интегрирования (рис. 5.8, б
)

После подстановки этого соотношения в соотношение (5.19) полу­чают

где — ордината искового графика углового ускорения;

Масштаб искомого графика ; единицы СИ: = мм; = мм/(рад с -2).

График функции строят по найденным значениям орди­нат для ряда позиций. Точки на кривой соединяют от руки плавной линией, а затем обводят с помощью лекала.

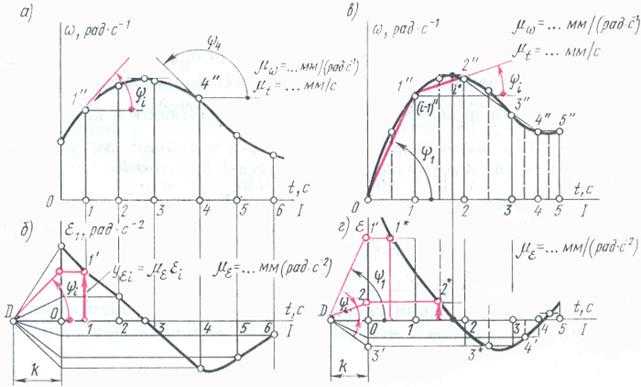
Графическое дифференцирование рассмотренным методом каса­тельных имеет относительно низкую точность. Более высокую точность получают при графическом диф­ференцировании методом хорд (рис. 5.8, в
и г
).

1
2
»

Остальные построения аналогичны ранее описанным при графи­ческом дифференцировании методом касательных. Выбирают отре­зок (мм); проводят лучи, наклоненные под углами до пересечения с осью ординат в точках 1
«, 2
«, 3
» … , которые переносят на ординаты, проведенные в середине каждого из интервалов. Полученные точки 1
*, 2
*, 3
* являются точками иско­мой функции .

Масштабы по осям координат при этом методе построения свя­заны таким же соотношением (5.21), которое было выведено для случая графического дифференцирования методом касательных.

Дифференцирование функции f(x)
, заданной (либо вычисленной) в виде массива чисел, выполняют методом численного дифферен­цирования с применением ЭВМ.

Чем меньше шаг в массиве чисел, тем точнее можно вычис­лить значение производной функции в этом интервале

Синтаксис СУММПРОИЗВ

Аргументами функции СУММПРОИЗВ являются массивы, т.е. заданные диапазоны. Их может быть сколько угодно. Перечисляя их через точку с запятой, мы задаем количество массивов, которые надо сначала перемножить, а затем просуммировать. Единственное условие: массивы должны быть равными по длине и однотипными (т.е. либо все горизонтальные, либо все вертикальные).

Простейший пример использования функции

Чтобы стало понятно, как и что считает команда, рассмотрим простой пример. Имеем таблицу с указанными длинами и ширинами прямоугольников. Нам нужно сосчитать сумму площадей всех прямоугольников. Если не пользоваться данной функцией, придется произвести промежуточные действия и сосчитать площадь каждого прямоугольника, а только потом сумму. Как мы и сделали.

Обратите внимание, что нам не понадобился массив с промежуточными итогами. В аргументах функции мы использовали только массивы с длиной и шириной, а функция их автоматически перемножила и просуммировала, выдав тот же результат = 70



Особенности оформления графиков в Excel

Несколько советов по оформлению графиков в Excel:

Первое, что следует сделать пользователю, — ввести правильно название зависимости. Для этого нужно выделить щелчком мыши блок «Название диаграммы», щёлкнуть по нему ещё раз и ввести требуемое наименование. При необходимости этот блок можно удалить, выделив его и нажав клавишу Delete.

Если требуется изменить не только название, но и стиль написания, следует, снова выделив блок, вызвать контекстное меню и выбрать в нём раздел «Шрифт». Подобрав подходящий вариант, юзер может нажимать на «ОК» и переходить к дальнейшим действиям.

Вызвав меню «Формат названия диаграммы», можно определить, в какой части рисунка будет располагаться наименование: в центре, в левом верхнем, нижнем правом углу и так далее.

Чтобы добавить на график названия осей, следует щёлкнуть мышью по «плюсику» справа от рисунка и в выплывающем списке установить галочку в соответствующем чекбоксе.

Если изначальное расположение названий не устраивает пользователя, он может свободно перетаскивать их по полю графика, а также менять их наименования описанным ранее способом.

Чтобы добавить на любую линию графика подписи (размещаются прямо на сетке) или выноски данных (в отдельных окошечках), нужно выделить её щелчком правой клавишей мыши и выбрать соответствующий параметр во вложенном меню «Добавить подписи данных».

Юзер может свободно сочетать способы размещения подписей, выбирая любой из пунктов в расширенном меню окошка «Элементы диаграммы».

Выбрав в том же меню «Дополнительные параметры», в боковом меню следует указать категорию представленных данных: простые числа, дроби, проценты, деньги и так далее.

Чтобы добавить таблицу с данными непосредственно на график, нужно вызвать нажатием на «плюсик» всё те же «Дополнительные параметры» и установить галочку в одноимённом чекбоксе.

Сетку, позволяющую найти значения графика в каждой точке, с помощью того же меню можно совсем убрать или добавить на неё основную и вспомогательную разметку.

«Легенда» — не самый полезный, но привычный блок графиков Excel. Убрать или перенести его можно, сняв галочку в окне «Дополнительные параметры» или вызвав вложенное меню. Более простой вариант — выделить блок щелчком мыши и нажать клавишу Delete или перетащить по полю графика.

Понять общее направление движения графика поможет линия тренда; добавить её для каждого ряда значений можно в том же окне.

Перейдя на вкладку «Конструктор», пользователь может кардинально изменить вид графика, выбрав один из стандартных шаблонов в разделе «Стили диаграмм».

А вызвав находящееся там же меню «Изменить цвета» — подобрать палитру для каждой линии в отдельности или для всего графика в целом.

Меню «Стили» вкладки «Формат» позволяет найти оптимальное представление для текстовых элементов графика.

Изменить фон, оставив нетронутым тип диаграммы, можно с помощью раздела «Стили фигур».

На этом настройку графика можно считать оконченной. Пользователь может в любой момент изменить тип диаграммы, перейдя в одноимённое меню и выбрав понравившийся вариант.

Необходимые инструменты Excel для вычисления производных

Вычисление производных в Excel может быть достаточно простым, если вы знакомы с несколькими необходимыми инструментами и функциями. Вот список нужных компонентов, которые вы должны использовать:

Ячейки	В Excel производные рассчитываются с помощью арифметических операций над значениями ячеек. Убедитесь, что вы используете ячейки для хранения значений, над которыми нужно выполнить операцию производной.
Функции	Excel имеет набор встроенных функций для выполнения разных математических операций. Для вычисления производных могут потребоваться функции, такие как SUM, PRODUCT, POWER и т. д.
Формулы	Вычисление производных осуществляется с использованием специальных формул. В Excel вы можете вводить формулы, которые сочетают функции, значения ячеек и операторы для выполнения нужных вычислительных операций.
Покоординатные ссылки	Для вычисления производных с использованием Excel вы должны использовать покоординатные ссылки. То есть, когда вы вводите формулы, убедитесь, что они правильно ссылается на ячейки, используя координаты столбцов и строк, например, A1, B2 и т. д.
Сохранение формул	Excel автоматически поддерживает сохранение формул, когда вы копируете их в другие ячейки. Это очень полезно, когда вы хотите вычислить производные для нескольких значений одновременно.

Используя эти инструменты, вы сможете легко вычислять производные в Excel. Заполните ячейки значениями, используйте нужные функции и формулы, и ваша таблица Excel будет готова для проведения расчетов производных.

Минимум теории.

Производная определяет скорость изменения функции, описывающей какой-либо процесс во времени или в пространстве.

Предел отношения изменения в точке функции к изменению переменной при стремлении изменения переменной к нулю называется производной непрерывной функции.

y’ ( x )=lim ( Δy / Δx ) при Δx →0

Геометрический смысл производной функции в точке – это тангенс угла наклона к оси x касательной к графику функции в этой точке.

tg ( α )= Δy / Δx

Если функция дискретная (табличная), то приближенное значение ее производной в точке находят с помощью конечных разностей.

Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.

В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.

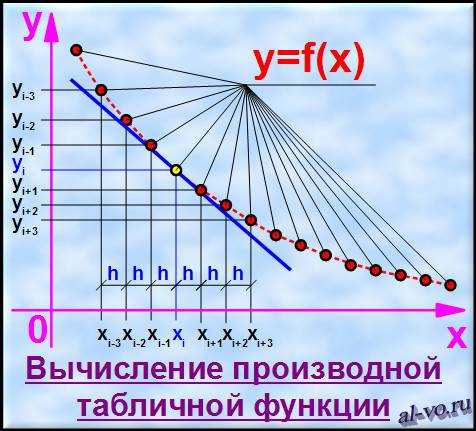
Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.

Моделирования касательной в заданной точке функции

В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.

Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:

где к = /'(хо) — угловой коэффициент;

Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (х_мин и х_макс) и ординат (у_мин и у_макс).

Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х₂,у₂), которые располагаются на границах прямоугольника.

Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х) . Значения углового коэффициента

могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.

Пусть к > 0. Остановимся на всех возможных вариантах расположения точек. При х_х = х_мин с учетом формулы у_х = к * (х_мин — х) + у .

Если выполняется неравенство у_мин у_макс задаем у_г = у_макс и вычисляем х_г = (у_макс — у + к * хук.

Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем х₂= х_макс и у₂ = к * (х_макс — х) + у.

Если выполняется неравенство у_мин и подсчитываем х₂ = (у_макс — у + к * х)//с.

Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)

Формируем таблицы начальных условий задачи.

координат заданной точки функции(х, у) (F2 и G2);

углового коэффициента к = /'(х) (Н2);

граничных значений диапазонов (х_мин, х_макс, у_мин, у_макс) (A2:D5).

Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения у_г при х_г = х_мин и у₂ при х₂ = х_макс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).

Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы — Точечная, а вид — Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.

Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.

Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у — к * х. Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.

Изменяя значения координаты х, осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.

При необходимости можно дополнительно построить график производной заданной функции.