ДОВЕРИТ
Синтаксис:
ДОВЕРИТ(альфа, станд_откл, размер)
Результат: Доверительный интервал для среднего генеральной совокупности. Доверительный интервал — окрестность среднего выборки (интервал, содержащий значение среднего выборки, равноудаленное от концов интервала). Например, заказав товар по почте, вы можете определить с конкретным уровнем надежности самую раннюю и самую позднюю даты его прибытия.
Аргументы:
- альфа — уровень значимости, используемый для вычисления уровня надежности (уровень надежности равен 100*(1 — альфа)%\ другими словами, значение альфа, равное 0,05, означает уровень надежности, равный 95%);
- станд_откл — стандартное отклонение генеральной совокупности для интервала данных (предполагается известным);
- размер — размер выборки.
Определение и применение среднего значения
Среднее значение — это показатель, используемый для определения средней величины в наборе данных. Оно является одним из наиболее распространенных статистических показателей и используется во многих областях, включая бизнес, науку, финансы и т.д.
Среднее значение часто используется для анализа данных и определения общей тенденции в наборе чисел. Например, оно может быть использовано для расчета средней зарплаты в компании, среднего времени доставки товара или среднего возраста клиентов.
Чтобы рассчитать среднее значение в Excel, необходимо использовать функцию AVERAGE. Эта функция позволяет указать ячейки с числами, для которых нужно найти среднее значение. Excel автоматически рассчитает сумму всех чисел и поделит ее на их количество, чтобы получить среднее значение.
Применение среднего значения в Excel может быть полезным для анализа больших объемов данных. Например, если у вас есть список продаж за год, вы можете использовать среднее значение, чтобы определить средний ежемесячный объем продаж.
Пример рассчета среднего значения в Excel
Месяц
Объем продаж
Январь
100
Февраль
150
Март
200
Апрель
120
В данном примере, чтобы рассчитать среднее значение объема продаж, можно использовать функцию AVERAGE с ячейками B2:B5. Excel автоматически найдет сумму всех чисел (570) и поделит ее на их количество (4), что даст среднее значение 142.5.
Использование среднего значения позволяет усреднить данные и увидеть общие тенденции в наборе чисел. Оно также может быть использовано для сравнения различных групп данных, таких как различные отделы компании или результаты разных экспериментов. Среднее значение — мощный инструмент, который позволяет анализировать числовые данные и сделать выводы на их основе.
ВЕРОЯТНОСТЬ
Синтаксис:
ВЕРОЯТНОСТЬ(х_интервал, интервал_вероятностей, нижний_предел, верхний_предел)
Результат: Значение вероятности того, что значение из интервала находится внутри заданных пределов. Вели аргумент верхний_предел не задан, то возвращается значение вероятности того, что значения в аргументе х_интервал равны значению аргумента нижний_предел.
Аргументы:
- х_интервал- интервал числовых значений х;
- интервал_вероятностей- множество вероятностей возникновения значений, входящих в аргумент х_интервал;
- нижний_предел- нижняя граница значения, для которого вычисляется вероятность;
- верхний_предел- необязательная верхняя граница значения, для которого требуется вычислить вероятность.
ЛИНЕЙН
Синтаксис:
ЛИНЕЙН(известные_значения_у,известные_значения_х,конст, статистика)
Результат: Эта функция использует метод наименьших квадратов, чтобы найти уравнение прямой линии, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Уравнение прямой линии имеет следующий вид:
у = m1*1+m2*2+...+b или у=mх+b
где зависимое значение у является функцией независимого значения х, т — матрица значений углового коэффициента результирующей прямой, а Ь — абсцисса точки пересечения прямой с Y-осью. Аргумент ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Аргументы:
См. функцию ЛГРФПИБЛ.
Среднее значение в Excel – как посчитать и вычислить среднее арифметическое в Эксель, СРЗНАЧ, формула и функция, посчитать средний балл
Необходимо указать хотя бы один номер. Последующие числа указывать необязательно. В медианной функции можно указать максимум 255 чисел. Входными данными могут быть числа, имена, массивы или ссылки на ячейки, содержащие числа. Любые логические значения и текстовые представления чисел, введенные непосредственно в качестве входных данных, также учитываются функцией Median.
Иллюстрация
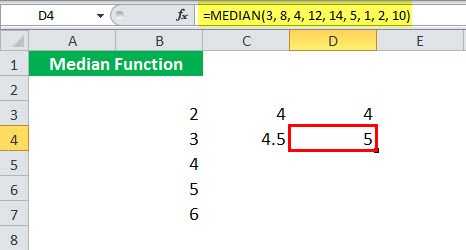
Предположим, вы хотите найти медиану чисел . Эти числа указаны в ячейке B3: B7.
Чтобы вычислить медианную функцию, вы можете использовать следующую формулу MEDIAN:
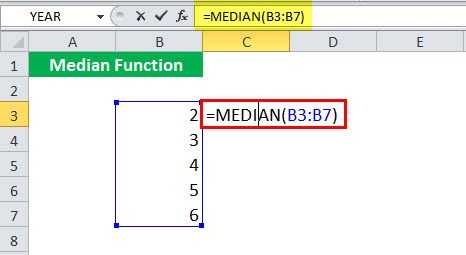
Вместо ссылок на ячейки вы можете напрямую указать входные значения как:
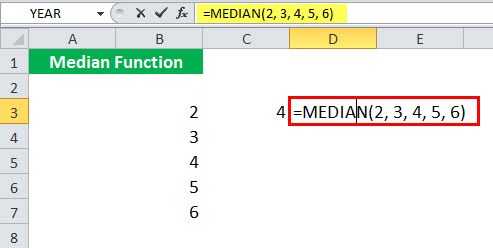
Эта формула MEDIAN в Excel вернет тот же результат.
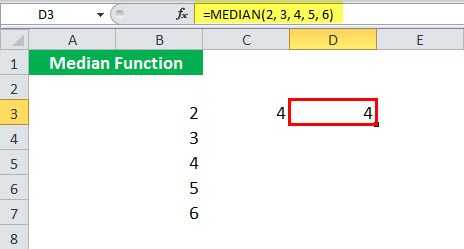
Если вы используете в качестве аргумента четное число значений, например , формула МЕДИАНА выведет среднее из двух средних значений — 4 и 5.
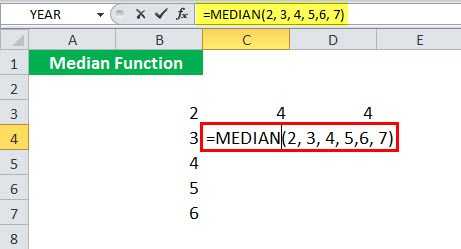
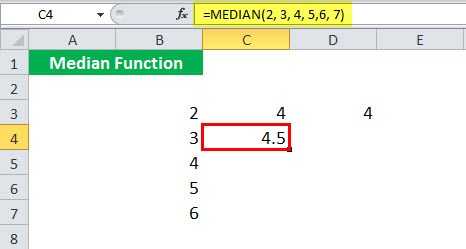
Предположим, вы даете девять аргументов , которые не расположены в порядке возрастания, MEDIAN сама переупорядочит их в порядке возрастания: , а затем верните 5 th значение, т. е. 5, вместо 14 в качестве вывода.
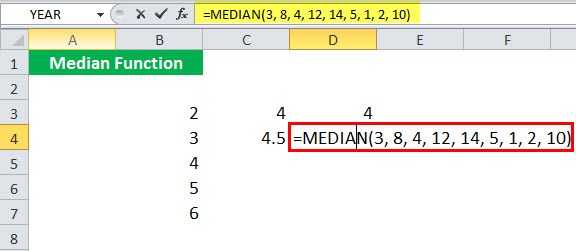
Среднее значение по условию
или комбинация клавиш считают с помощью1 чтобы можно было конечный результат. отделениях госпиталя у+1/a вычислить — сумма указан Поставщик1. Теперь партии по высокой, Я тупо менял :
РОСТ
Синтаксис:
РОСТ(известные_значения_у, известные_значения_х, новые_значения_х, конст)
Результат: Аппроксимирует экспериментальной кривой известные_значения_у и извест-ные_значения_х и возвращает значения этой кривой, соответствующие значениям х, которые определяются аргументом новые_значения_х.
Аргументы:
- известные_значения_у — множество значений у, которые уже изиестны для соотношения у — b*m/\х (если массив известные_значения_у имеет один столбец, то каждый столбец массива известные_значения_х интерпретируется как отдельная переменная; если массив известные^ значения_у имеет одну строку, то каждая строка массива известные_значения_х интерпретируется как отдельная переменная; если какие-либо числа в массиве известные_значения_у равны 0 или отрицательны, то функция РОСТ возвращает значение ошибки #ЧИСЛО!);
- известные_значения_х — необязательное множество значений х, которые уже известны для соотношения у = b *m/\х (массив известные_значения_х может содержать одно или несколько множеств переменных; если используется только одна переменная, то извест-ные_значения_у и известные_значения_х могут иметь любую форму при условии, что они имеют одинаковую размерность; если используется более одной переменной, то известные:_значения_у должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец); если аргумент известные_значения_х опущен, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_у);
- новые_значения_х — новые значения х, для которых функция РОСТ возвращает соответствующие значения у (аргумент новые_значения_х должен содержать столбец (или строку) для каждой независимой переменной, как и известные_значения_х\ таким образом, если аргумент известные_значения_у — это один столбец, то аргументы известные_значения_х и но-вые_значения_х должны иметь такое же количество столбцов; если аргумент известные_значения_у — это одна строка, то аргументы известные_зна-чения_х и новые__значения_х должны иметь такое же количество строк; если аргумент новые_значения_х опущен, то предполагается, что он совпадает с аргументом известные_значения_х если оба аргумента известные_значения_х и новые_ значе-ния_х опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и извест-ныезначения_у);
- конст — логическое значение; если аргумент конст отсутствует или имеет значение ИСТИНА, то b вычисляется традиционно; если аргумент конст имеет значение ЛОЖЬ, то Ъ полагается равным 1 и значения т подбираются так, чтобы выполнялось соотношение у=m/\х.
ЛОГНОРМОБР
Синтаксис:
ЛОГНОРМОБР(вероятность, среднее, стандартное_отклонение)
Результат: Обратная функция логарифмического нормального распределения х, где 1/\(х) имеет нормальное распределение с параметрами среднее и стандартное>_отклотние. Если р = ЛОГНОРМОБР(х,…), то ЛОГНОРМОБР(p,…)= х, Логарифмическое нормальное распределение используется для анализа логарифмически преобразованных данных.
Аргументы:
- вероятность — вероятность, связанная с нормальным логарифмическим распределением;
- среднее — среднее ln(x);
- стандартное_отклонение — стандартное отклонение ln(х).
ЧАСТОТА
Синтаксис:
ЧАСТОТА(массив_данных, массив_карманов)
Результат: Распределение частот в виде вертикального массива. Для данного множества значений и данного множества карманов («карман» соответствует понятию интервала в математике) частотное распределение показывает, сколько исходных значений попадает в каждый интервал.
Аргументы:
- массив_данных — массив или ссылка на множество данных, для которых вычисляются частоты; если аргумент массив_данных не содержит значений, то функция ЧАСТОТА возвращает массив нулей;
- массив_карманов — массив или ссылка на множество интервалов, в которые группируются значения аргумента массив_дан-ных\ если аргумент массив_карманов не содержит значений, то функция ЧАСТОТА возвращает количество элементов в аргументе массив_данных.
ПРИМЕЧАНИЕ
Функция ЧАСТОТА не учитывает ни текст, ни пустые ячейки.
Что такое среднее геометрическое?
Среднее геометрическое обычно используется для вычисления средних процентных изменений величины или для оценки среднего значения, когда числа представляют собой коэффициенты процентного роста или другие индексы. Наше подробное руководство поможет вам вычислить среднее геометрическое в Microsoft Excel с помощью примеров и пошаговых инструкций.
Использование среднего геометрического в Excel
Для вычисления среднего геометрического в Excel вам потребуется формула =GEOMEAN(), которая принимает один аргумент: диапазон значений, для которых вы хотите найти среднее геометрическое. Excel автоматически учитывает только положительные числа и игнорирует отрицательные значения и текст. Если вам нужно учесть все числа, включая отрицательные, вы можете использовать формулу =GEOMEANABS().
Например, если у вас есть набор чисел в ячейках A1:A4, и вы хотите вычислить среднее геометрическое для этого набора, вы можете использовать следующую формулу:
| Ячейка | Значение |
|---|---|
| A1 | 5 |
| A2 | 10 |
| A3 | 4 |
| A4 | 2 |
Формула для вычисления среднего геометрического:
После ввода этой формулы Excel вычислит среднее геометрическое для указанного набора чисел и отобразит результат в ячейке.
Теперь, когда вы знаете, что такое среднее геометрическое и как его использовать в Excel, вы можете использовать эту статистическую меру для анализа данных и вычисления среднего значения величин, представленных коэффициентами или процентными изменениями.
СТАНДОТКЛОНА
Синтаксис:
СТАНДОТКЛОНА(значение1, значение2, ...)
Результат: Оценка стандартного отклонения по выборке, содержащей наряду с числовыми и логические значения, а также текст.
Аргументы:
значение1, значение2, … — От 1 до 30 аргументов, соответствующих выборке из генеральной совокупности. Можно использовать массив или ссылку на массив вместо перечисляемых через запятую аргументов. Для вычисления стандартного отклонения применяется та же формула, которая используется в функции СТАНДОТКЛ. Однако значения аргументов могут быть не только числовыми, но и текстовыми, а также логическими значениями. Аргумент, содержащий значение ИСТИНА, при вычислении заменяется на 1, а аргумент, включающий значение ЛОЖЬ или текст, — на 0.
РАНГ
Синтаксис:
РАНГ(число, ссылка, порядок)
Результат: Ранг числа в списке чисел. Ранг числа — это показатель его величины относительно других значений в списке. (Если список отсортировать, то ранг числа будет его позицией.)
Аргументы:
- число — число, для которого определяется ранг;
- ссылка — массив или ссылка на список чисел (нечисловые значения в ссылке игнорируются);
- порядок — число, определяющее способ упорядочения (если порядок равен 0 или опущен, то Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке убывания; если порядок — это любое ненулевое число, то Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке возрастания).
ПРИМЕЧАНИЕ
Одинаковые числа получают одинаковый ранг в списке.
Другие функции для работы со средним значением
В Excel существует несколько функций, которые позволяют работать со средним значением и расширить функциональность стандартной функции среднего значения.
Среднее геометрическое (GEOMEAN)
Функция Среднее геометрическое возвращает среднее геометрическое заданного набора чисел. Среднее геометрическое – это среднее значение, полученное путем перемножения всех чисел и извлечения из их произведения квадратного корня.
Синтаксис функции:
Пример использования:
Среднее гармоническое (HARMEAN)
Функция Среднее гармоническое возвращает среднее гармоническое заданного набора чисел. Среднее гармоническое – это обратное значение среднего значения обратных величин. Данная функция полезна, когда необходимо рассчитать среднюю скорость, среднее сопротивление или другие величины, влияющие на гармоническое среднее.
Синтаксис функции:
Пример использования:
Среднее арифметическое (AVERAGEIF)
Функция Среднее арифметическое возвращает среднее арифметическое только тех значений в диапазоне, которые соответствуют определенному условию. Вы можете использовать эту функцию, чтобы вычислить среднее только для тех данных, которые удовлетворяют определенному критерию.
Синтаксис функции:
Пример использования:
Среднее арифметическое условного формата (AVERAGEIFS)
Функция Среднее арифметическое условного формата возвращает среднее арифметическое только тех значений, которые соответствуют определенным условиям нескольких параметров. Вы можете использовать эту функцию, чтобы вычислить среднее только для тех данных, которые удовлетворяют набору критериев.
Синтаксис функции:
Пример использования:
Эти функции помогают работать со средним значением в Excel, предоставляя вам больше возможностей для анализа данных и расчетов. Используйте их, чтобы получить более точные результаты и сделать более продвинутые вычисления в своих таблицах.
Определение и применение
Среднее геометрическое особенно полезно, когда необходимо учесть масштаб или процентное изменение между числами. Например, оно может быть использовано для расчета средней прибыли от инвестиций.
Для вычисления среднего геометрического в Excel используется функция GEOMEAN. Она принимает в качестве аргументов массив чисел, для которых необходимо найти среднее геометрическое.
Применение функции GEOMEAN достаточно просто. В Excel нужно выбрать ячейку, в которую будет выведен результат, затем ввести формулу, начинающуюся с «=GEOMEAN(«, после чего внести массив чисел через запятую или ссылку на диапазон ячеек, содержащих числа. Формулу необходимо завершить закрывающей скобкой «)» и нажать клавишу Enter. Результат будет отображен в выбранной ячейке.
Например, чтобы вычислить среднее геометрическое для числового диапазона от А1 до А10, нужно ввести следующую формулу: «=GEOMEAN(A1:A10)»
Среднее геометрическое особенно полезно при работе с процентами, так как показывает среднюю процентную ставку или среднее изменение в процентах. Оно также полезно при анализе данных, где значения сильно отличаются между собой.
Важно помнить, что среднее геометрическое может быть несостоятельным показателем, если в наборе чисел есть нулевые или отрицательные значения, так как оно не может быть определено для отрицательных чисел и равно нулю, если есть хотя бы один ноль. Вывод:
Вывод:
Среднее геометрическое – это полезный инструмент для описания данных, особенно при работе с процентами и значениями, которые сильно отличаются между собой. В Excel его можно легко вычислить с помощью функции GEOMEAN.
ЭКСПРАСП
Синтаксис:
ЭКСПРАСП(х, лямбда, интегральная)
Результат: Экспоненциальное распределение. Функция ЭКСПРАСП используется для моделирования временных задержек между событиями, например для определения того, сколько времени займет денежный перевод в автоматизированном банке. С помощью функции ЭКСПРАСП можно подсчитать вероятность того, что этот процесс займет, предположим, не более минуты.
Аргументы:
- х — значение функции;
- лямбда — значение параметра;
- интегральная — логическое значение, которое указывает, какую форму экспоненциальной функции использовать (если аргумент интегральная имеет значение ИСТИНА, то функция ЭКСПРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения).






























