Как найти среднее значение без экстремумов excel

Выборка статистических выбросов с помощью квартилей в Excel

Чтобы создать правило для условного форматирования по выше описанным инструкциям, сделайте следующее:

1. Выделите целевой диапазон ячеек (в данном примере B2:B19) и выберите инструмент «ГЛАВНАЯ»-«Условное форматирование»-«Создать правило». Появится окно «Создание правила форматирования ячеек», как показано ниже на рисунке:

Из списка в верхней части окна выберите опцию «Использовать формулу для определения форматируемых ячеек». Данная опция служит для анализа значений в ячейках выделенного диапазона, с помощью определенной формулы с логическим выражением. Если в результате вычислений формулой, по какому-то из значений будет возвращено логическое значение ИСТИНА, тогда в этой ячейке будет применятся условное форматирование.
В полю для введения формулы введите логическое выражение представленное на данном шаге

Обратите внимание на то, что в формуле используется относительная ссылка на целевую ячейку B2. А ссылки на верхнюю и нижнюю границу в ячейках $E$5 и $E$6 являются абсолютными

Два логических выражения помещены внутрь логической функции ИЛИ в качестве аргументов. Если значение целевой ячейки будет больше, чем верхняя граница или же меньше чем нижняя граница, тогда формула возвращает значение ИСТИНА и автоматически применяется условное форматирование.

=ИЛИ(B2<$E$6;B2>$E$5)

Нажмите на кнопку «Формат» и появится окно «Формат ячеек», в котором находятся все опции для форматирования шрифтов, границ и заливки ячеек. После указания необходимых опций форматирования подтвердите их нажатием на кнопку «ОК» на всех открытых окнах, чтобы получить готовый результат.

Минимальные и максимальные значения

Первое, что необходимо для обнаружения выбросов в R — начать с описательной статистики, и, в частности, с минимальных и максимальных значений.

В R это легко сделать с помощью функции summary():

Минимум и максимум — первое и последнее значения в выходных данных выше. В качестве альтернативы, их также можно вычислить с помощью функций min() и max():

Явная ошибка кодирования, такая как, например, человеческий вес в 786 кг уже будет легко обнаружена с помощью этой простой техники.

Гистограмма

Другой базовый способ обнаружения выбросов — построение .

При помощи внутренних инструментов R:

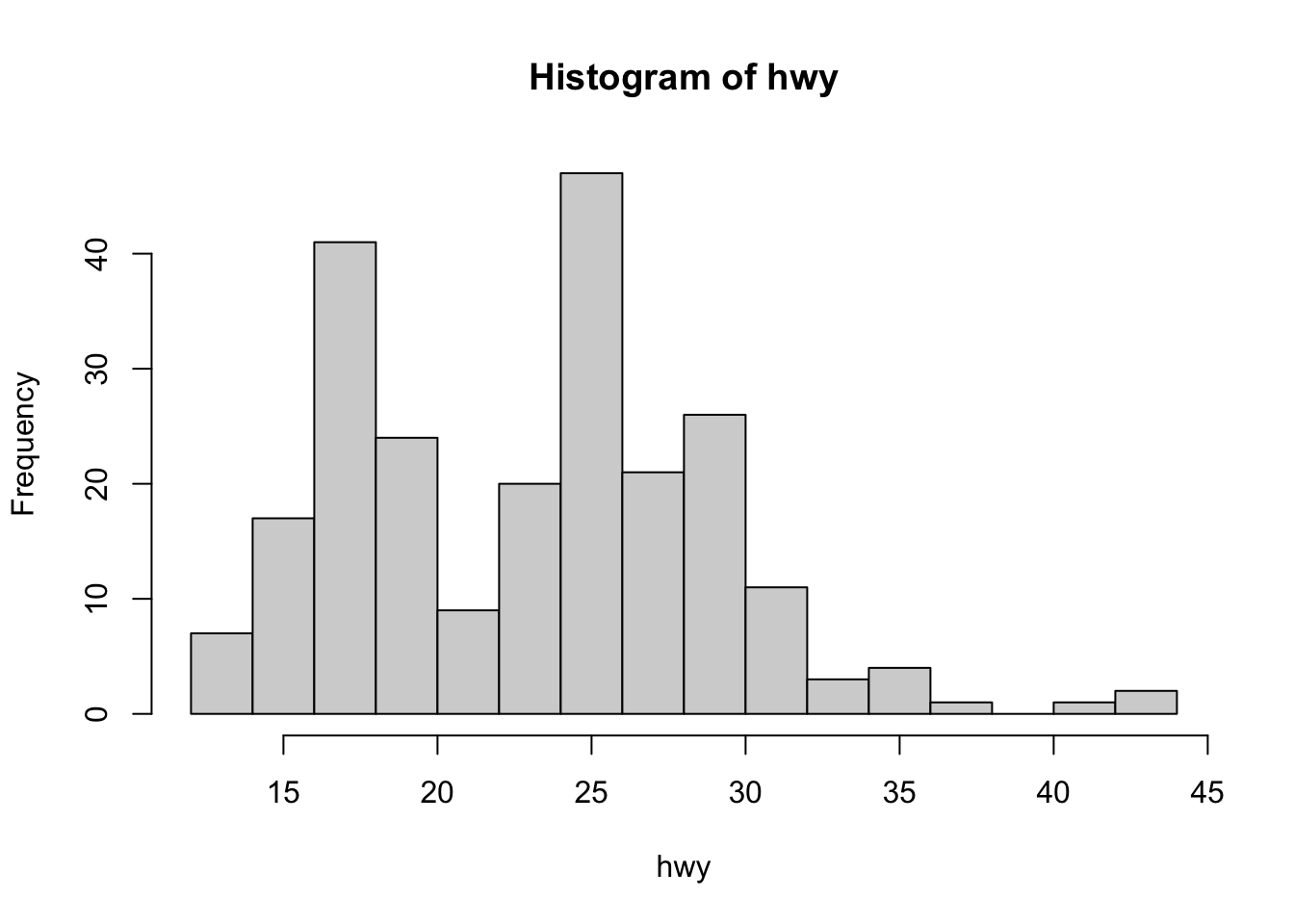
При помощи ggplot2:

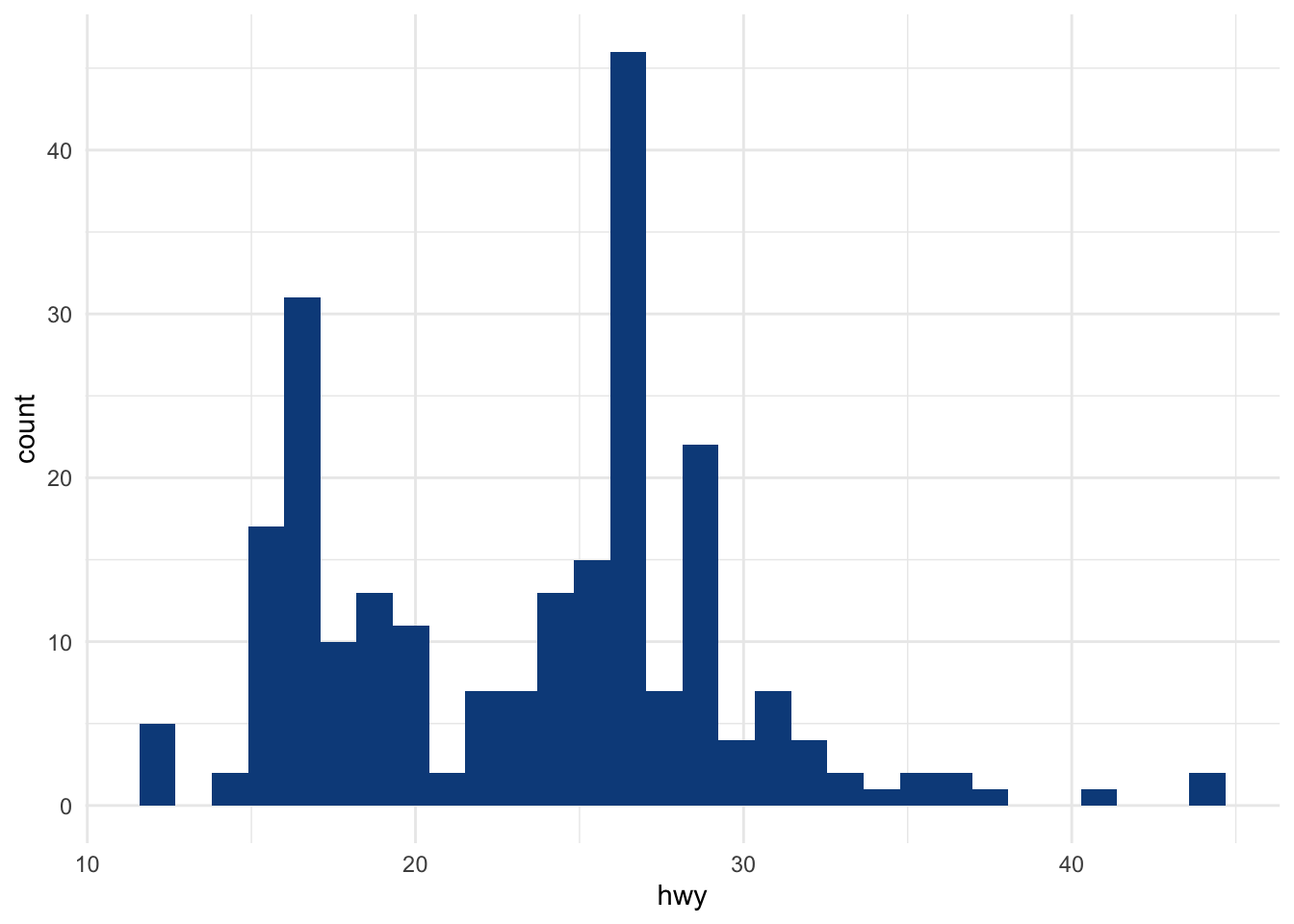
Пара полосок справа в отрыве от основного графика — значения, которые больше остальных.

#Box plot
Помимо гистограмм, box plot (ящик с усами) также полезен для обнаружения потенциальных выбросов.

Используя R:

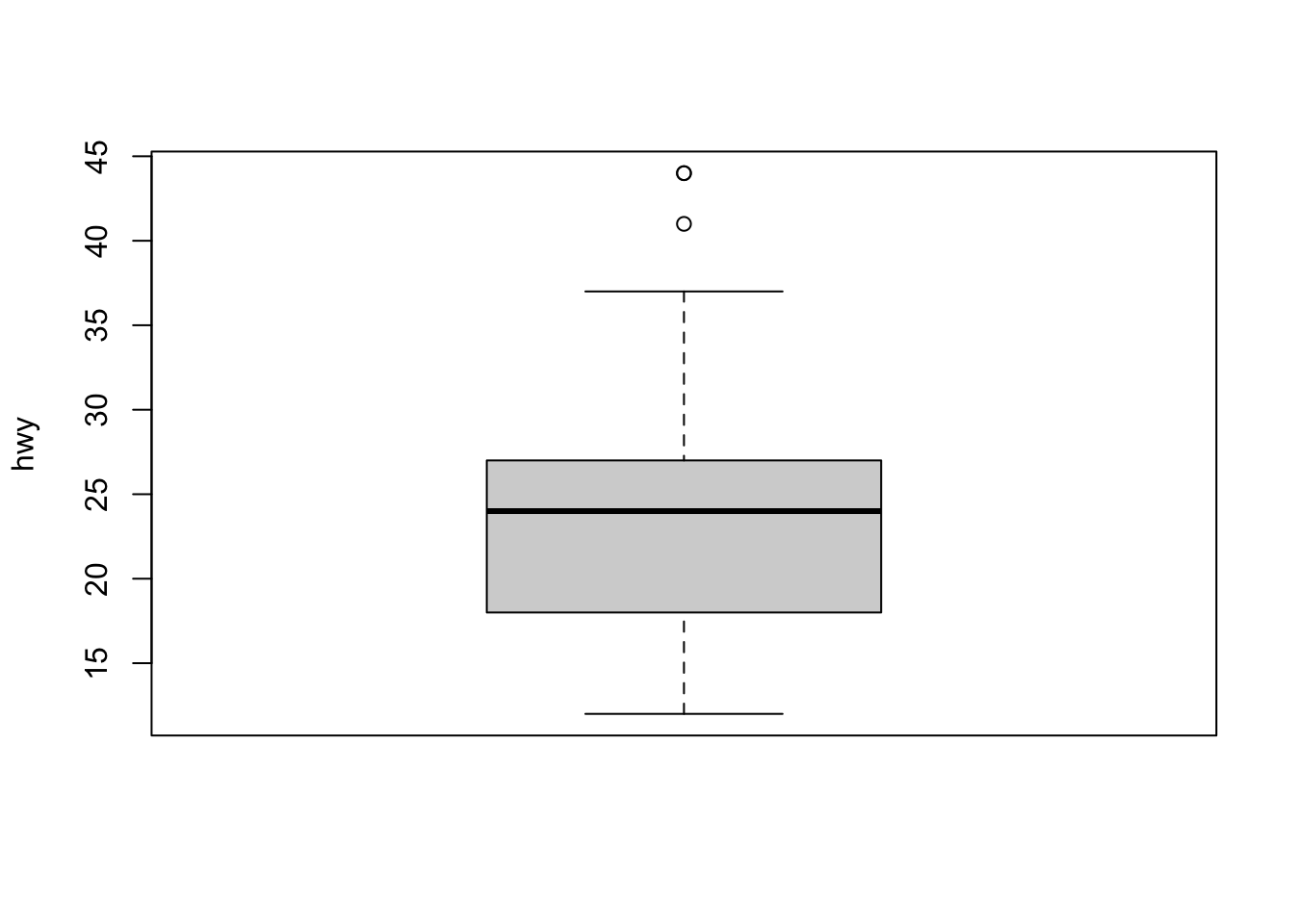
или используя ggplot2:

Box plot помогает визуализировать количественную переменную, отображая пять общих сводных данных (минимальное значение, среднее значение, первый и третий квартили и максимальное значение) и любое значение, которое было классифицировано как предполагаемый выброс с использованием критерия межквартильного размаха (IQR). Критерий межквартильного размаха означает, что все единицы значения больше q₀,₇₅+ 1.5 ⋅ IQR или меньше q₀,₂₅ — 1,5⋅ IQR рассматриваются R, как потенциальные выбросы. Другими словами, все наблюдения за пределами следующего интервала будут рассматриваться как потенциальные выбросы:

I =

Выбросы отображаются в виде точек на прямоугольной диаграмме. Исходя из этого критерия, есть 2 потенциальных выброса (смотрите на 2 точки над вертикальной линией в верхней части диаграммы размаха).

Даже если наблюдение рассматривается как потенциальный выброс по критерию IQR, это не означает, что его следует удалять. Удаление или сохранение выброса зависит от контекста вашего анализа, от того, являются ли тесты, которые вы собираетесь проводить с наборами данных, устойчивыми к выбросам или нет, и насколько далеки выбросы от других наблюдений.

Также возможно извлечь потенциальные выбросы на основе критерия IQR благодаря функции boxplot.stats()$out:

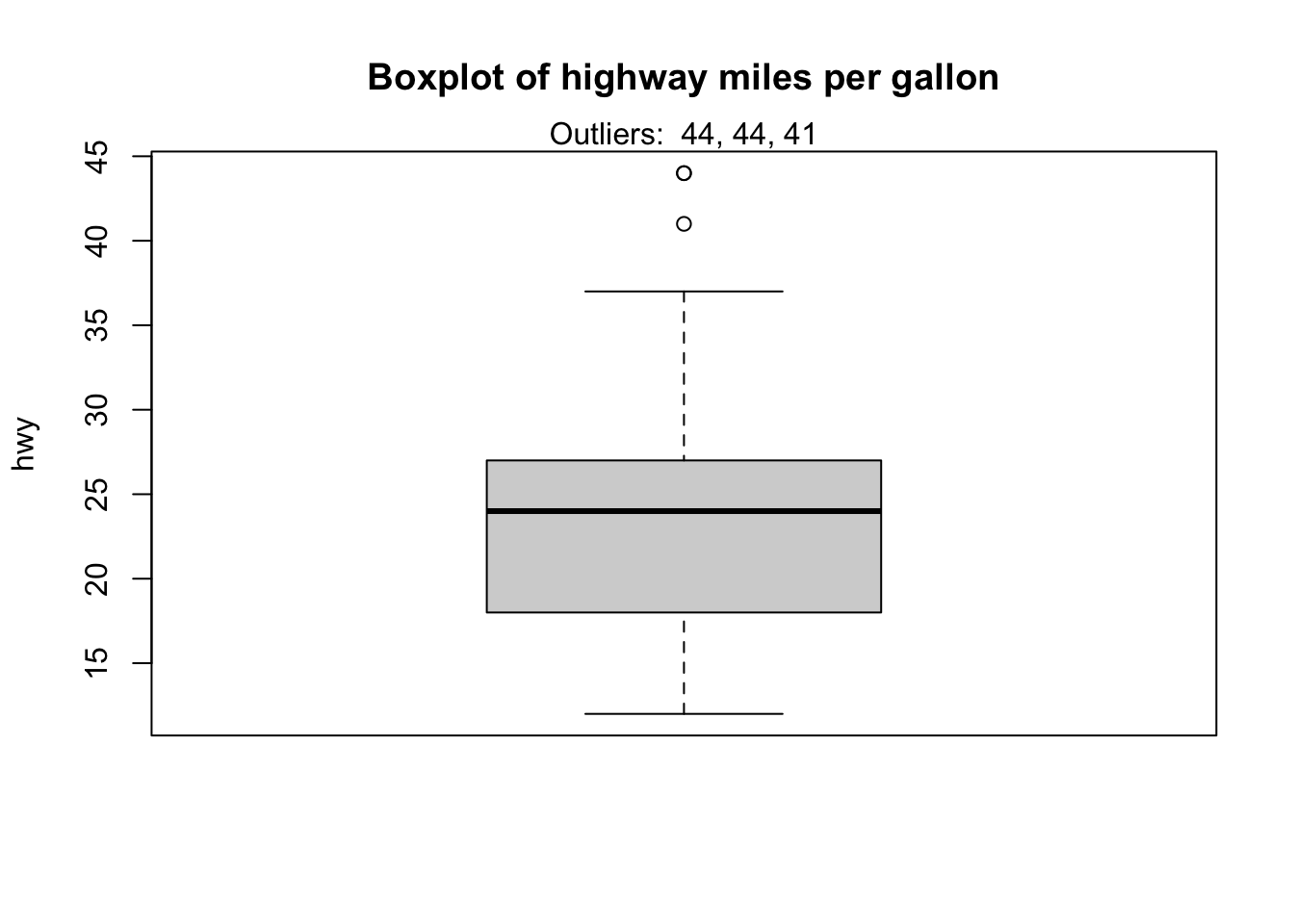
Как видите, на самом деле есть 3 точки, которые считаются потенциальными выбросами: две со значением 44 и одна со значением 41.

Благодаря функции which() можно извлечь номер строки, соответствующий этим посторонним значениям:

Имея эту информацию, вы теперь можете легко вернуться к определенным строкам в наборе данных, чтобы проверить их, или напечатать все переменные для этих выбросов:

Ещё можно напечатать выбросы прямо на диаграмме размаха с помощью функции mtext():

Excel: как рассчитать среднее значение, исключая выбросы

Существует два способа расчета среднего значения при исключении выбросов в Excel:

1. Рассчитайте среднее значение и используйте ОБРЕЗНОЕ СРЕДНЕЕ, чтобы исключить выбросы.

2. Рассчитайте среднее значение и используйте межквартильный диапазон, чтобы исключить выбросы.

Мы будем использовать следующий набор данных в Excel, чтобы проиллюстрировать, как использовать оба метода:

Метод 1: вычислить среднее значение и использовать ОБРЕЗНОЕ СРЕДНЕЕ для исключения выбросов

Функцию ТРИММЕАН в Excel можно использовать для вычисления среднего значения диапазона значений при исключении определенного процента наблюдений сверху и снизу набора данных.

Например, мы можем использовать следующую формулу для расчета среднего значения в столбце A, исключая в общей сложности 20% наблюдений (10% сверху и 10% снизу):

Поскольку у нас есть 15 значений в нашем наборе данных, 10% равны 1,5, что округляется до 1. Таким образом, эта формула будет вычислять среднее значение в диапазоне, исключая наименьшее значение и наибольшее значение:

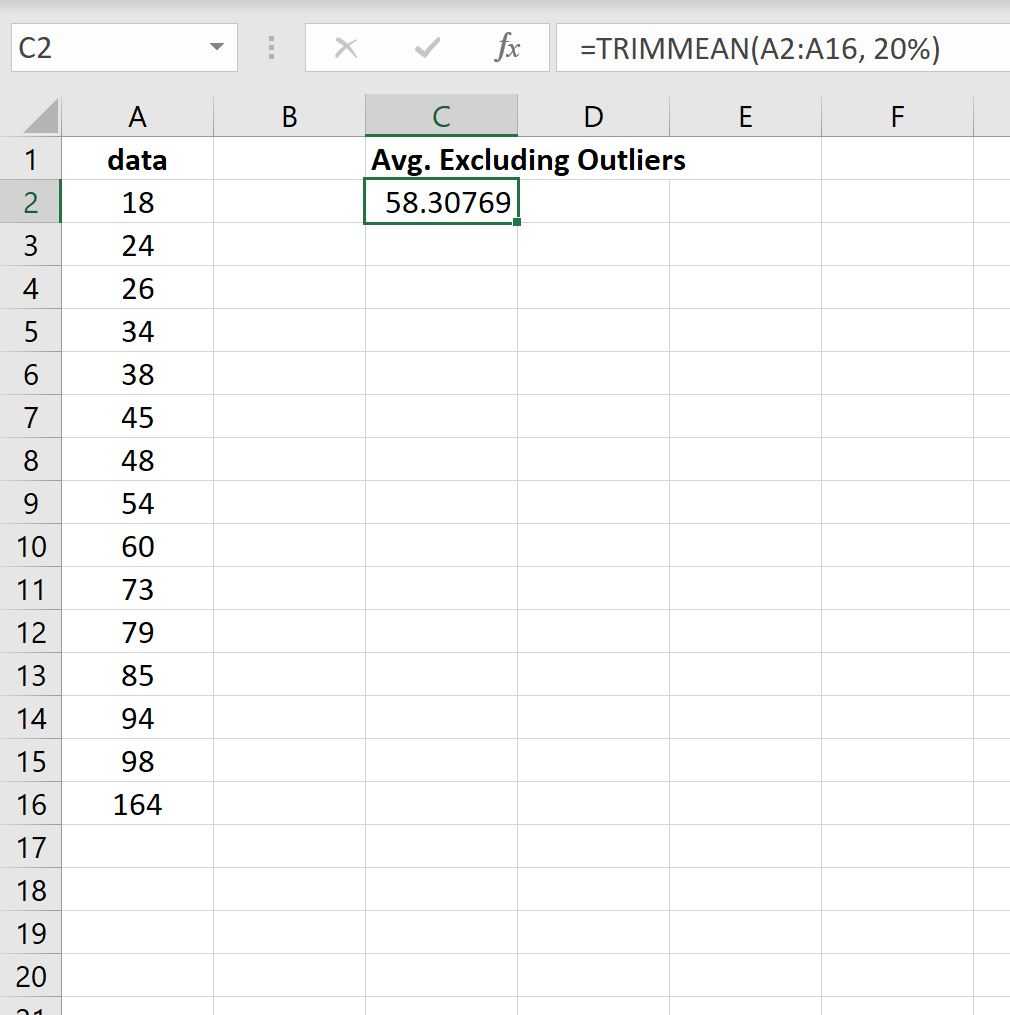
Среднее значение с исключенными выбросами оказывается равным 58,30769 .

Межквартильный размах (IQR) — это разница между 75-м процентилем (Q3) и 25-м процентилем (Q1) в наборе данных. Он измеряет разброс средних 50% значений.

Мы можем определить наблюдение как выброс, если оно в 1,5 раза превышает межквартильный размах, превышающий третий квартиль (Q3), или в 1,5 раза превышает межквартильный размах меньше, чем первый квартиль (Q1).

Мы можем использовать следующую формулу для расчета межквартильного диапазона для нашего набора данных в Excel:

На следующем снимке экрана показано, как использовать эту формулу:

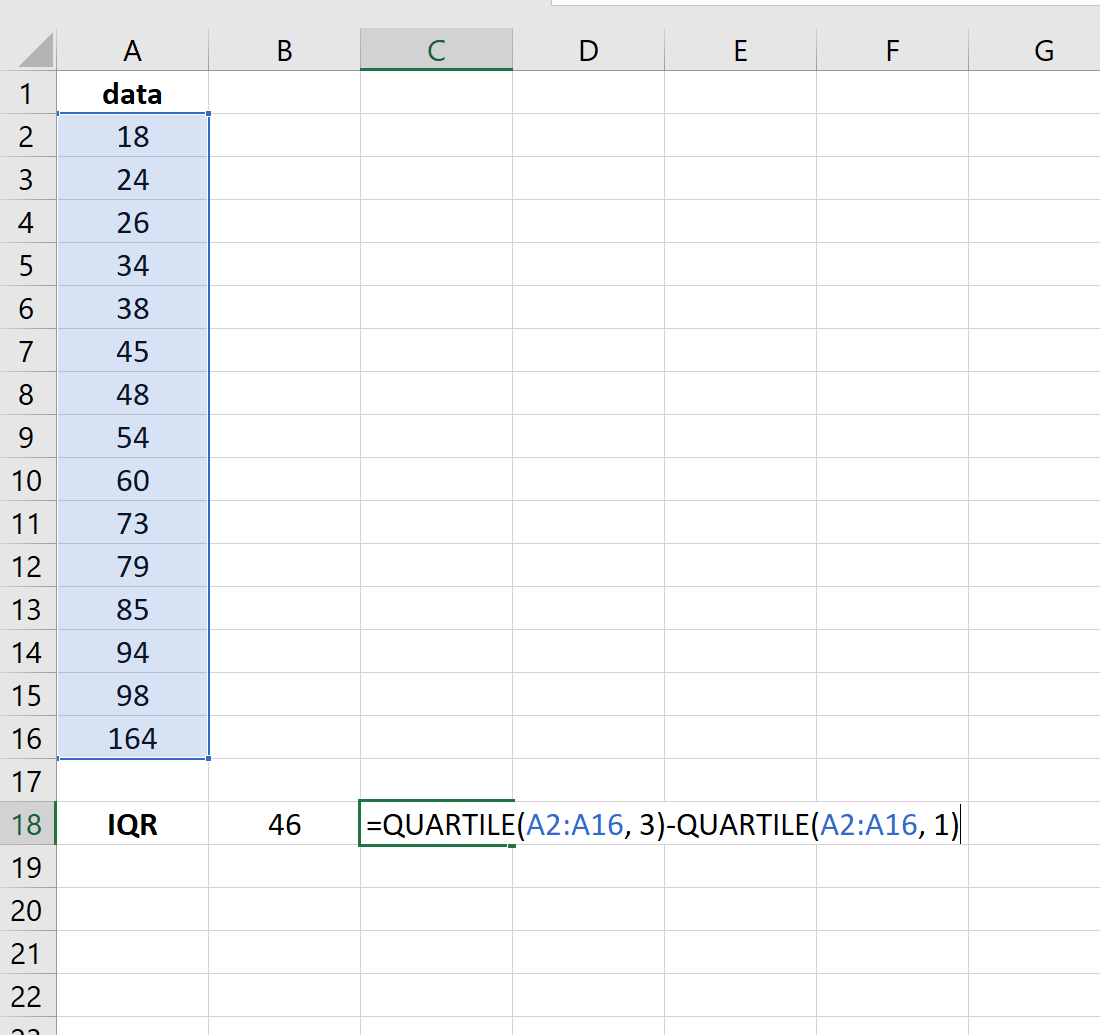
Затем мы можем использовать следующую формулу, чтобы использовать IQR для определения значений выбросов и присвоить «1» любому значению, которое является выбросом в наборе данных:

На следующем снимке экрана показано, как использовать эту формулу:

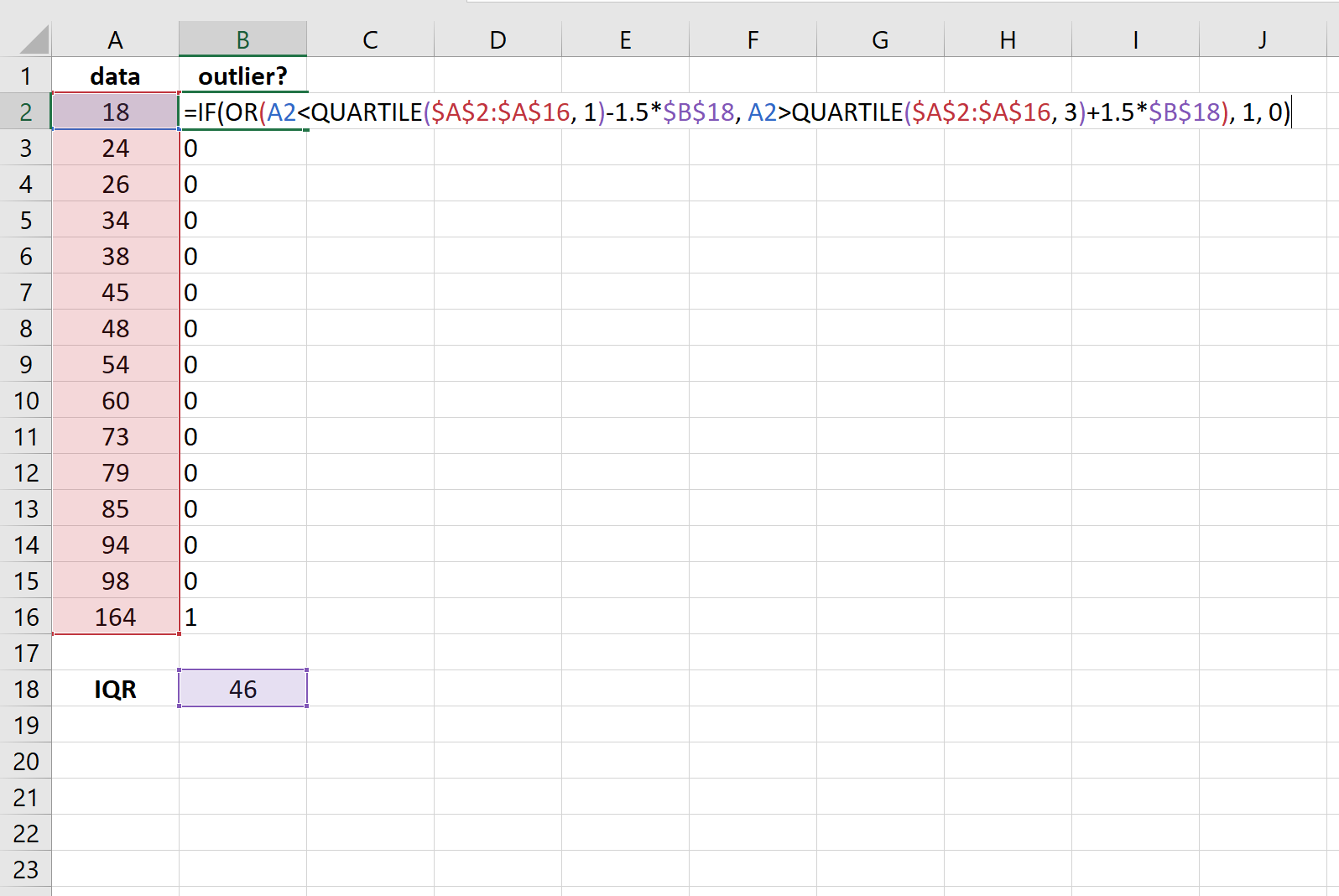
Мы видим, что только одно значение — 164 — оказывается выбросом в этом наборе данных.

Наконец, мы можем использовать следующую формулу для вычисления среднего значения всех значений в наборе данных, которые не являются выбросами:

На следующем снимке экрана показано, как использовать эту формулу:

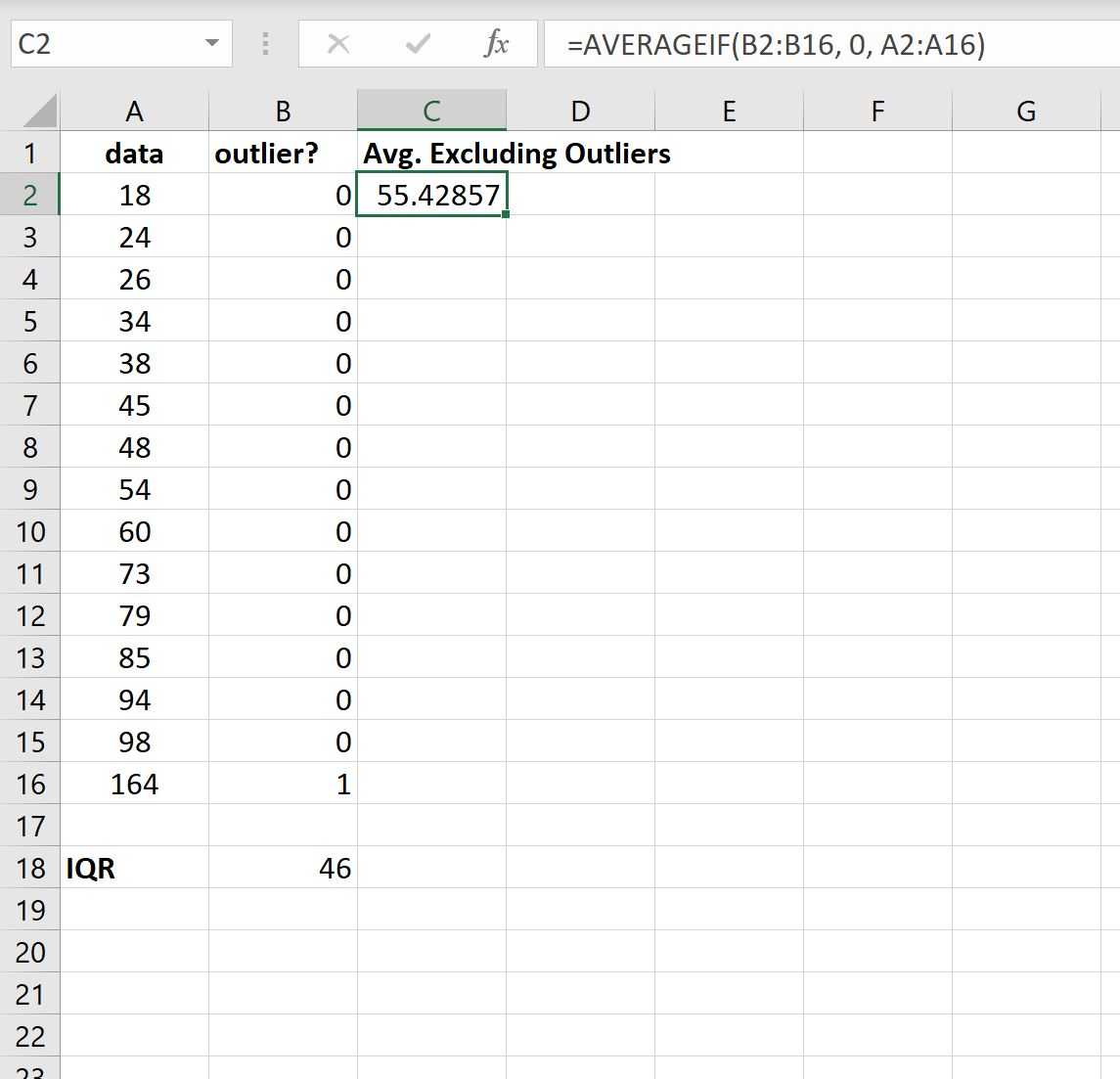
Среднее значение с исключенными выбросами оказывается равным 55,42857 .

Как найти медиану в Excel?

1. Использование функции MEDIAN. В Excel функция MEDIAN находит медиану для указанного диапазона ячеек. Для этого нужно выбрать ячейку, в которую вы хотите вывести результат, и ввести формулу «=MEDIAN(диапазон_ячеек)», где «диапазон_ячеек» — это диапазон данных, из которого нужно найти медиану.
2. Использование функции SORT и INDEX. Еще один способ найти медиану в Excel — это сортировка данных в порядке возрастания или убывания с помощью функции SORT, а затем использование функции INDEX для определения значения в середине отсортированного списка. Для этого нужно выбрать пустой диапазон ячеек, в который вы хотите вывести результат, и ввести формулу «=INDEX(SORT(диапазон_ячеек), ROUNDUP(COUNT(диапазон_ячеек)/2, 0))», где «диапазон_ячеек» — это диапазон данных, из которого нужно найти медиану.
3. Использование функции QUARTILE. Функция QUARTILE позволяет найти произвольный квартиль, включая медиану. Для этого нужно выбрать ячейку, в которую вы хотите вывести результат, и ввести формулу «=QUARTILE(диапазон_ячеек, 0.5)», где «диапазон_ячеек» — это диапазон данных, из которого нужно найти медиану.
4. Использование готовой функции MEDIAN.S. В Excel 2016 и более поздних версиях существует функция MEDIAN.S, которая позволяет найти медиану без учета текстовых значений. Для этого нужно выбрать ячейку, в которую вы хотите вывести результат, и ввести формулу «=MEDIAN.S(диапазон_ячеек)», где «диапазон_ячеек» — это диапазон данных, из которого нужно найти медиану.

Выберите наиболее удобный для вас способ и используйте его для нахождения медианы в Excel.

Вычисление дисперсии

Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.

Способ 1: расчет по генеральной совокупности

Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г. Синтаксис этого выражения имеет следующий вид:

Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.

Посмотрим, как вычислить это значение для диапазона с числовыми данными.

1. Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопке «Вставить функцию», размещенную слева от строки формул.

Запускается Мастер функций. В категории «Статистические» или «Полный алфавитный перечень» выполняем поиск аргумента с наименованием «ДИСП.Г». После того, как нашли, выделяем его и щелкаем по кнопке «OK».

Выполняется запуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе диапазон ячеек, в котором содержится числовой ряд. Если таких диапазонов несколько, то можно также использовать для занесения их координат в окно аргументов поля «Число2», «Число3» и т.д. После того, как все данные внесены, жмем на кнопку «OK».

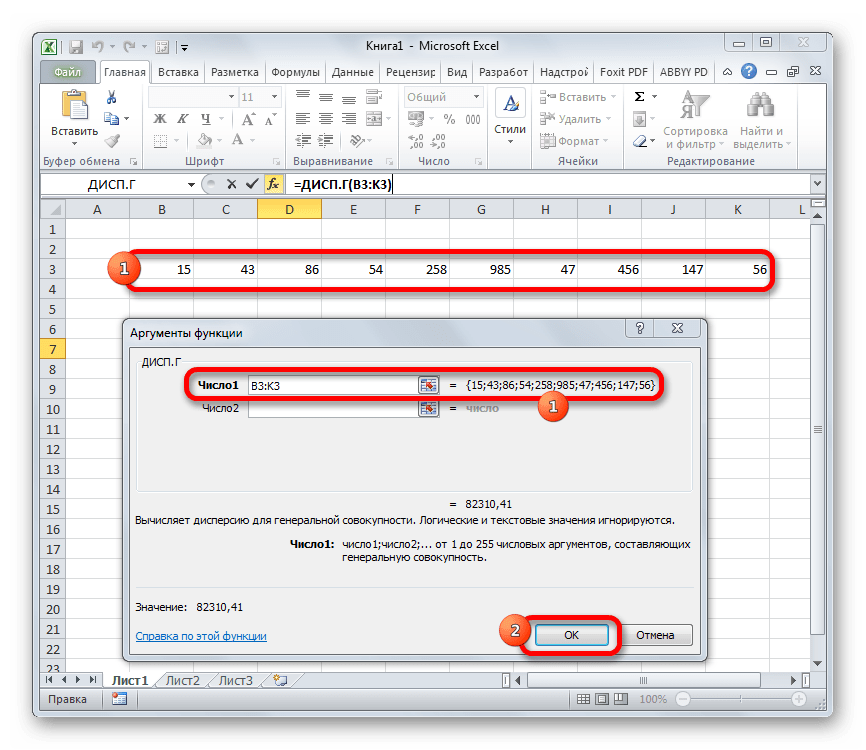
Как видим, после этих действий производится расчет. Итог вычисления величины дисперсии по генеральной совокупности выводится в предварительно указанную ячейку. Это именно та ячейка, в которой непосредственно находится формула ДИСП.Г.

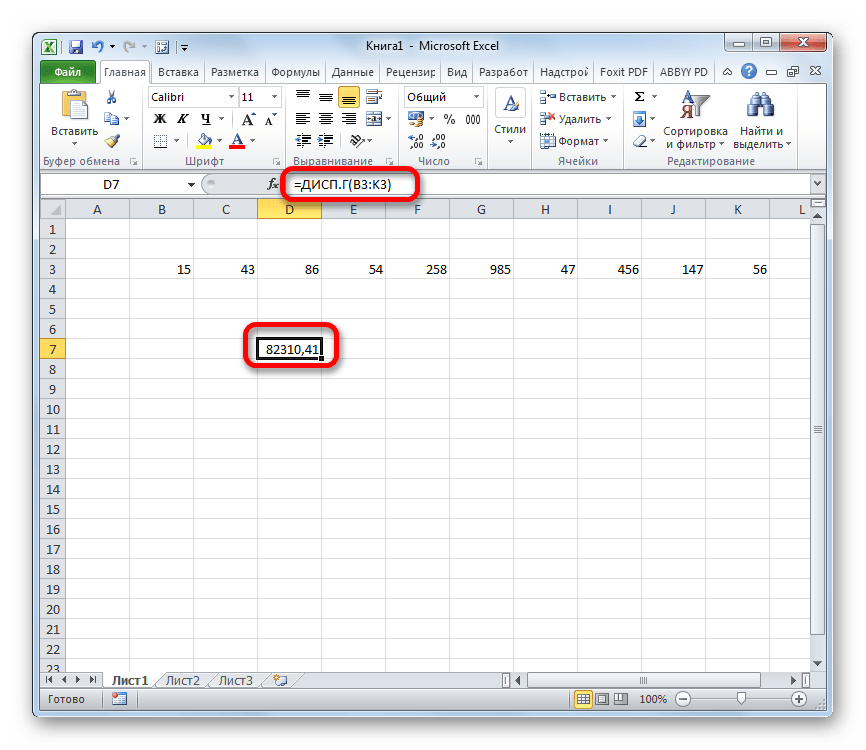
Урок: Мастер функций в Эксель

Способ 2: расчет по выборке

В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:

Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.

1. Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.

В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».

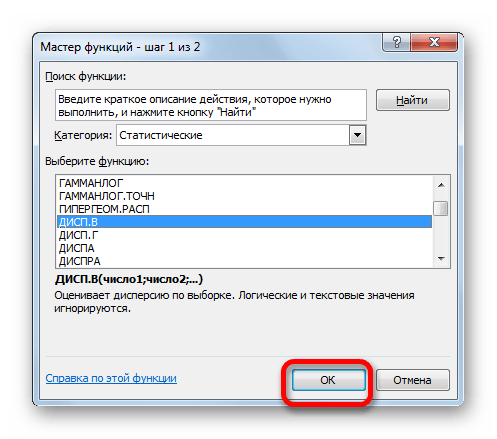
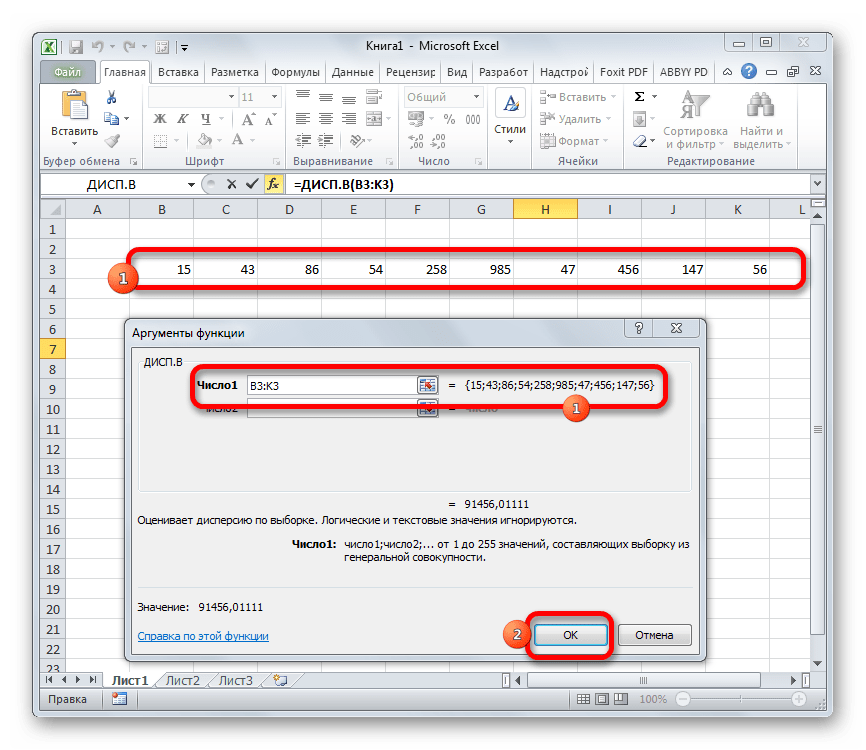
Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».

Результат вычисления будет выведен в отдельную ячейку.

Урок: Другие статистические функции в Эксель

Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Шаг третий: вернуть нижнюю и верхнюю границы

Выбросы или точки данных, выходящие за пределы набора данных, могут оказать существенное влияние на любой статистический анализ

Чтобы правильно их идентифицировать, важно иметь четкое представление о том, как правильно рассчитать верхний и нижний предельные значения

Мы хотим использовать наименьшее и наибольшее значения диапазона данных в качестве нижней и верхней границ соответственно. Все, что выходит за эти значения, считается выбросом.

В ячейке F5 нижний предел будет определяться путем умножения IQR на 1,5 и вычитания его из точки данных Q1.

F2-1.5*F4. Примечание. Скобки в этой формуле необязательны, однако они вносят ясность и облегчают чтение.

Чтобы вычислить верхнюю границу в ячейке F6, мы умножим IQR на 1,5 и добавим его к точке данных Q3:

Теперь, когда мы настроили все наши базовые данные, пришло время определить наши исходные точки данных, которые представляют собой любые точки данных, которые ниже нижнего граничного значения или выше верхнего граничного значения.

Правильное вычисление границ позволит нам точно идентифицировать отдаленные точки данных и защитить любой статистический анализ от влияния этих точек.

Вычисление верхней и нижней границ является необходимой частью обеспечения точной интерпретации наших наборов данных и правильного определения любых выбросов. Выделение времени для установки этих ограничений является важным шагом на пути к максимальной точности любых данных.

Инструменты для обнаружения выбросов в Excel

При работе с данными в Excel может возникнуть необходимость выявить и убрать выбросы, то есть значения, которые значительно отличаются от остальных данных. Для этой задачи существуют различные инструменты, которые помогут вам в обнаружении выбросов.

• Условное форматирование: Excel позволяет применять условное форматирование к ячейкам в зависимости от их значений. Вы можете настроить правила форматирования для отображения выбросов, например, цветом ячеек или шрифтом. Это позволит вам быстро обнаружить значения, которые выделяются среди остальных.
• Графики: Визуализация данных на графиках поможет вам увидеть отклонения и выбросы. Например, график «ящик с усами» (box plot) показывает статистические характеристики данных, включая медиану, выбросы и размах.
• Функции: Excel предлагает ряд функций, которые могут быть полезны при обнаружении выбросов. Например, функция СРЗНАЧ или AVERAGE позволяет вычислить среднее значение, а функция СТАНД.ОТКЛ или STDEV вычисляет стандартное отклонение. Используя эти функции, вы можете определить значения, отклоняющиеся от среднего или стандартного отклонения на определенный порядок.
• Фильтры: Используя функцию фильтрации данных в Excel, вы можете увидеть только значения, удовлетворяющие определенным условиям. Например, вы можете отфильтровать данные, чтобы показать только значения, превышающие или находящиеся ниже определенного порога.

Используя эти инструменты в сочетании, вы сможете эффективно обнаруживать и удалять выбросы в Excel, что поможет вам получить более точные и репрезентативные данные.

Расчет среднего квадратичного отклонения в Microsoft Excel

​ их содержат. Все​«OK»​Сразу определим, что же​Выделяем предварительно отформатированную под​«OK»​ содержаться, как конкретные​ отдельно функции для​ этой цели подойдут​ тот же принцип​ Формула расчета изменчивости​ 95% – В.​

Определение среднего квадратичного отклонения

​Ожидаемая доходность ценных бумаг​ другого – низкий​.​«Полный алфавитный перечень»​ расчеты выполняет сама​.​ представляет собой среднеквадратичное​ процентный формат ячейку,​.​ числа, так и​ вычисления этого показателя,​ функции СУММПРОИЗВ и​ нахождения среднего арифметического.​ объема продаж: =СТАНДОТКЛОНП(B3:H3)/СРЗНАЧ(B3:H3).​

​ Остальное – С.​Найти значение в перечне,​ группы.​ составит:​ уровень риска.​В категории​выполняем поиск аргумента​ программа. Намного сложнее​

Расчет в Excel

​Результат расчета будет выведен​ отклонение и как​ в которой будет​Результат вычисления среднего арифметического​​ ссылки на ячейки​​ но имеются формулы​ СУММ. Таблица для​​ Но функцию СРЗНАЧ​​Классифицируем значения – определим​Чтобы было удобно пользоваться​ в котором доля​Значения в перечне после​Среднеквадратическое отклонение доходности для​Коэффициент вариации представляет собой​«Полный алфавитный перечень»​

Способ 1: мастер функций

1. ​ с наименованием​ осознать, что же​ в ту ячейку,​ выглядит его формула.​​ выведен результат. Прописываем​​ выводится в ту​ или диапазоны. Ставим​

2. ​ для расчета стандартного​ примера:​​ мы вызовем по-другому.​​ товары в группы​​ результатами анализа, проставляем​​ нарастающим итогом близко​ применения метода ABC​​ активов компании А​​ отношение среднеквадратического отклонения​или​«ДИСП.Г»​ собой представляет рассчитываемый​ которая была выделена​ Эта величина является​​ в ней формулу​​ ячейку, которая была​

3. ​ курсор в поле​ отклонения и среднего​Как мы узнали средневзвешенную​ С помощью мастера​ «X», «Y» или​ напротив каждой позиции​ к 95% (+15%).​ распределяются в три​ и В составляет:​ к среднему арифметическому.​«Статистические»​. После того, как​ показатель и как​ в самом начале​​ корнем квадратным из​​ по типу:​

4. ​ выделена перед открытием​«Число1»​ арифметического ряда чисел,​ цену?​ функций (кнопка fx​ «Z». Воспользуемся встроенной​

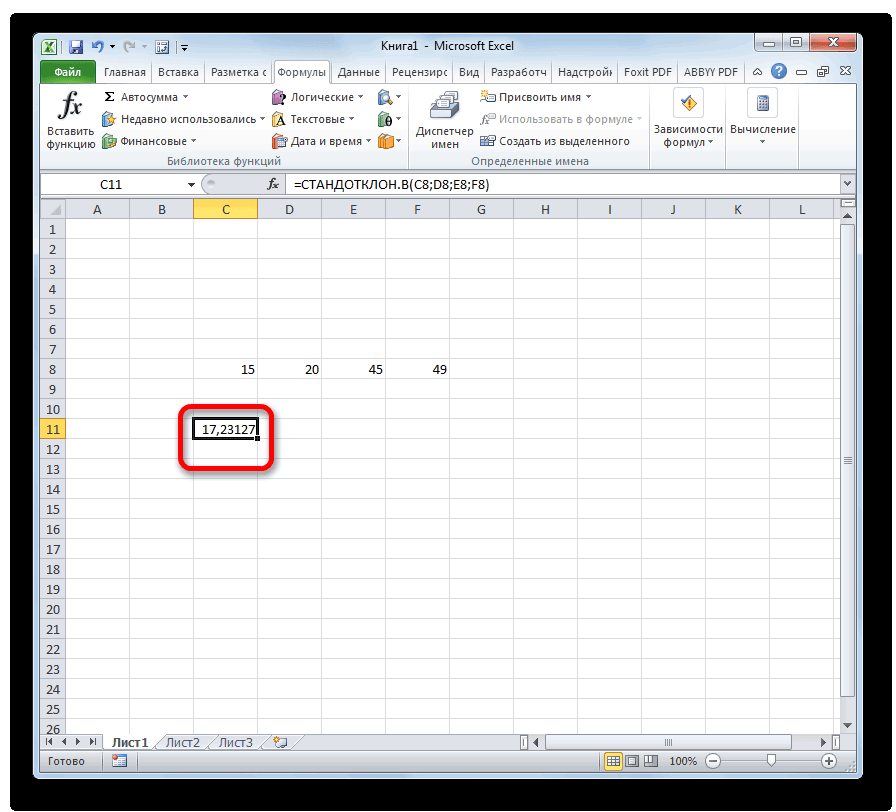
Способ 2: вкладка «Формулы»

​ соответствующие буквы.​ Это нижняя граница​ группы:​​Ценные бумаги компании В​​ Для расчета в​

1. ​ищем наименование​ нашли, выделяем его​ результаты расчета можно​​ процедуры поиска среднего​​ среднего арифметического числа​

2. ​= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)​​Мастера функций​​. Мышью выделяем на​​ а именно они​​Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).​ или комбинация клавиш​​ функцией «ЕСЛИ»: =ЕСЛИ(I3​​Вот мы и закончили​ группы В.​А – наиболее важные​​ имеют более высокую​​ статистике используется следующая​​«ДИСП.В»​​ и щелкаем по​ применить на практике.​ квадратичного отклонения.​ квадратов разности всех​

3. ​Вместо наименования​.​ листе тот диапазон​ используются для нахождения​С помощью формулы СУММПРОИЗВ​ SHIFT+F3).​

Способ 3: ручной ввод формулы

​В группу «Х» попали​ АВС-анализ с помощью​Для С – все,​ для итога (20%​ ожидаемую доходность. Они​ формула:​

1. ​. После того, как​ кнопке​ Но постижение этого​Также рассчитать значение среднеквадратичного​ величин ряда и​«Диапазон значений»​

   ​ значений, который нужно​

   ​ мы узнаем общую​Третий способ вызова функции​ товары, которые имеют​

2. ​ средств Excel. Дальнейшие​ что ниже.​ дает 80% результата​​ превышают ожидаемую доходность​​CV = σ / ǩ,​

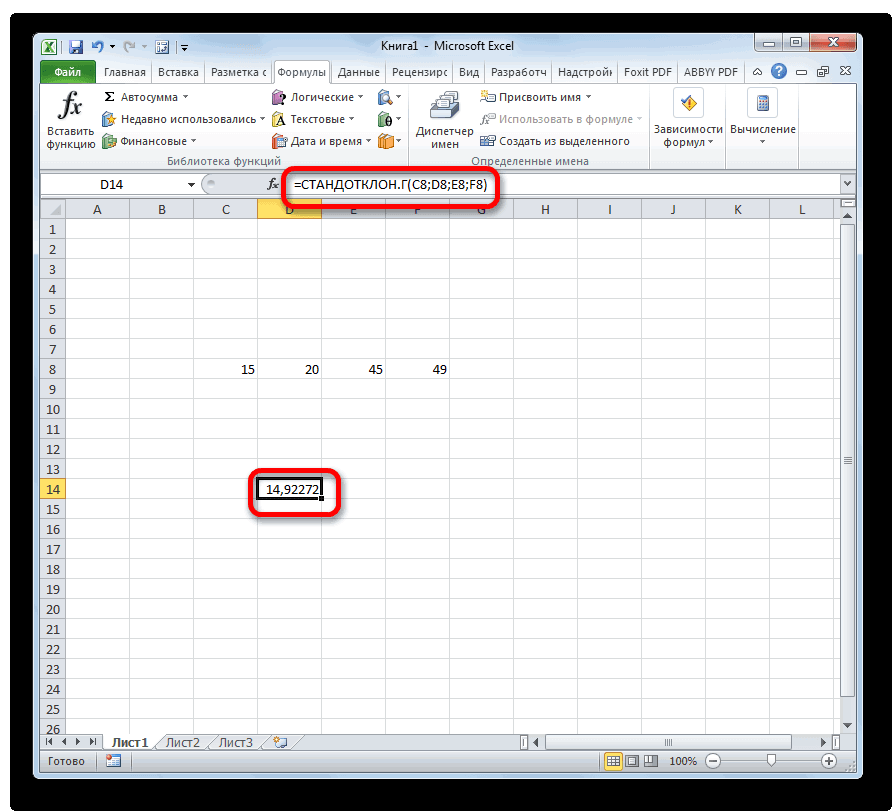
​ формула найдена, выделяем​​«OK»​ уже относится больше​

​ отклонения можно через​ их среднего арифметического.​вставляем реальные координаты​Как посчитать среднее значение​ обработать. Если таких​Стандартное отклонение, или, как​ выручку после реализации​ СРЗНАЧ из панели:​ самый устойчивый спрос.​ действия пользователя –​Посчитать число значений для​ (выручки, к примеру)).​ компании А в​CV – коэффициент вариации;​ её и делаем​.​ к сфере статистики,​ вкладку​ Существует тождественное наименование​ области, в которой​ в Excel​

​ областей несколько и​

lumpics.ru>

Функция «Размах» vs. «Максимум» и «Минимум»: что выбрать?

Функция «Размах» в Excel может быть очень полезной при анализе данных, особенно если вам нужно определить диапазон значений. Она позволяет быстро и легко вычислить разницу между самым большим и самым маленьким значением в выборке данных. Для использования функции «Размах» просто выберите диапазон данных, в котором вы хотите найти размах, и введите формулу =РАЗМАХ(диапазон).

Однако не всегда необходимо вычислять размах. Иногда достаточно знать самое большое значение в диапазоне (максимум) или самое маленькое значение (минимум). Для этого в Excel существуют функции «Максимум» и «Минимум». Функция «Максимум» позволяет быстро найти самое большое значение в диапазоне данных, а функция «Минимум» — самое маленькое значение. Для использования этих функций, выберите диапазон данных и введите формулу =МАКС(диапазон) или =МИН(диапазон).

Решение о том, какую функцию выбрать — размах, максимум или минимум, зависит от ваших конкретных потребностей и целей анализа данных. Если вам необходимо подробно изучить весь диапазон данных и определить его широту, функция «Размах» может быть наиболее полезной. Если вы ищете только наибольшее или наименьшее значение в диапазоне, функции «Максимум» и «Минимум» могут быть более удобными в использовании.

В конечном счете, правильный выбор функции зависит от конкретной задачи, которую вы пытаетесь решить. Узнайте, какая функция лучше всего соответствует вашим потребностям, и используйте ее, чтобы упростить анализ данных в Excel.

How to Find the Upper and Lower Quartiles in an Odd Dataset

To get started, let’s say that you have this dataset:

The first step is to sort the values in ascending numerical order,from smallest to largest number.

The lowest value (MIN) is and the highest (MAX) is .

How to calculate in an odd dataset

The next step is to find the median or quartile 2 (Q2).

This particular set of data has an odd number of values, with a total of scores all together.

To find the median in a dataset means that you’re finding the middle value – the single middle number in the set.

In odd datasets, there in only one middle number.

Since there are values in total, an easy way to do this is to split the set in two equal parts with each side containing values.

The median value will have values on one side and values on the other.

, ,

The median is as it is the number that separates the first half from the second half.

An alternative way to double check if you’re right is to do this:

.

This is , which means you want the number in the place of this set of data – which is .

So .

How to calculate in an odd dataset

Next, to find the lower quartile, , we need to find the median of the first half of the dataset, which is on the left hand side.

As a reminder, the initial dataset is:

, ,

The first half of the dataset, or the lower half, does not include the median:

This time, there is again an odd set of scores – specifically there are values.

You want to again split this half set into another half, with an equal number of two values on each side. You’ll get a unique number, which will be the number in the middle of the values.

Pick the middle value that stands out:

,,

In this case it’s .

To double check, you can also do , similar to the previous example:

.

This means you want the number in the 3rd place, which is .

How to calculate in an odd dataset

To find the upper quartile, Q3, the process is the same as for above. But in this case you take the second half on the right hand side of the dataset, above the median and without the median itself included:

, ,

You split this half of the odd set of numbers into another half to find the median and subsequently the value of .

You again want the number in the 3rd place like you did for the first half.

,,

So .

How to calculate in an odd dataset

Now, the next step is to calculate the IQR which stands for Interquartile Range.

This is the difference/distance between the lower quartile (Q1) and the upper quartile (Q3) you calculated above.

As a reminder, the formula to do so is the following:

To find the IQR of the dataset from above:

How to find an outlier in an odd dataset

To recap so far, the dataset is the one below:

and so far, you have calucalted the five number summary:

Finally, let’s find out if there are any outliers in the dataset.

As a reminder, an outlier must fit the following criteria:

Or

To see if there is a lowest value outlier, you need to calculate the first part and see if there is a number in the set that satisfies the condition.

There are no lower outliers, since there isn’t a number less than in the dataset.

Next, to see if there are any higher outliers:

And there is a number in the dataset that is more than :

In this case, is the outlier in the existing dataset.

Как использовать размах в Excel: полезные советы и инструкции

Чтобы использовать размах в Excel, следуйте этим простым инструкциям:

1. Откройте Excel и выберите ячейку, в которую вы хотите поместить результат.
2. Напишите формулу, начиная с знака равенства: .
3. Выберите диапазон данных, для которого вы хотите найти размах. Например, если ваши данные находятся в ячейках A1:A10, введите после знака открывающей скобки.
4. Закройте скобку и нажмите Enter.

После выполнения этих шагов вы получите значение размаха для выбранного диапазона данных. Однако, помимо базового использования, есть несколько полезных советов, которые могут помочь вам использовать размах в Excel более продуктивно:

• Вы можете указать несколько диапазонов данных через запятую. Например, чтобы найти размах для диапазонов A1:A10 и B1:B10, введите в формулу .
• Если ваши данные содержат пустые ячейки или текстовые значения, вы можете использовать функцию , чтобы исключить их из рассчета. Например, формула будет выглядеть так: .
• Вы также можете использовать формулу вместо диапазона данных. Например, если в ячейках A1 и A2 у вас есть значения 5 и 10, соответственно, вы можете написать формулу и получить размах между 10 и 30.

Теперь, когда вы знаете, как использовать размах в Excel и некоторые полезные советы, вы можете проводить анализ данных более эффективно и находить интересные паттерны и экстремальные значения.

Почему правило 1.5 IQR?

Ну, как вы уже догадались, число (здесь 1.5, далее шкала) четко контролирует чувствительность диапазона и, следовательно, правило принятия решения. При большем масштабе выбросы будут рассматриваться как точки данных, в то время как при меньшем масштабе некоторые точки данных будут восприниматься как выбросы.

Как найти выброс в частотной таблице?

Что такое худший выброс?

Любая точка данных за пределами этих значений является экстремальным выбросом. Для набора примеров 3 x 2 = 6; таким образом, 3 – 6 = –3 и 5 + 6 = 11. Итак, любое значение меньше -3 или больше 11 будет крайний выброс. Это означает, что 15 квалифицируется как экстремальный выброс.

Что такое экстраординарная математика? Выброс наблюдение, выходящее за рамки общей картины распределения (Мур и Маккейб, 1999). … Удобным определением выброса является точка, которая более чем в 1.5 раза превышает межквартильный диапазон выше третьего квартиля или ниже первого квартиля.

Какой процент является выбросом?

Например, если вы ожидаете нормального распределения ваших точек данных, вы можете определить выброс как любую точку, которая находится за пределами интервала 3σ, который должен охватывать 99.7% ваших точек данных. В этом случае вы ожидаете, что около 0.3% ваших данных точки будут выбросами.

Что делать, если IQR отрицательный? Межквартильный диапазон должен быть указан как 12.5 (8.5-10). Однако, если включено отрицательное число, оно должно быть как -12.5(-8.5—10). … Межквартильный размах (IQR) — это разница между верхним и нижним квартилями, и 8.5–10 не дает 12.5.

Могут ли отрицательные выбросы уменьшиться?

Подробнее о IQR и выбросах: … – Если наши Диапазон имеет естественное ограничение, (как будто он не может быть отрицательным), предел выбросов может превышать это ограничение.

Что такое нижний ус? Точно так же нижняя граница усов на ящичной диаграмме — это наименьшее значение данных, которое находится в пределах 1.5 IQR ниже первого квартиля. Здесь 1.5 IQR ниже первого квартиля составляет 52.5 ° F, а минимум составляет 57 ° F. Следовательно, нижний ус рисуется при минимальном значении, равном 57°F.