Как создать матрицу в excel с двумя осями

Основные функции Excel

1. SUM (СУММ)

Функция SUM используется для сложения значений в заданном диапазоне ячеек. Например, формула «=SUM(A1:A5)» сложит значения из ячеек A1, A2, A3, A4 и A5.

2. AVERAGE (СРЗНАЧ)

Функция AVERAGE вычисляет среднее значение заданного диапазона ячеек. Например, формула «=AVERAGE(A1:A5)» определит среднее значение для ячеек A1, A2, A3, A4 и A5.

3. MAX (МАКС)

Функция MAX находит максимальное значение в заданном диапазоне ячеек. Например, формула «=MAX(A1:A5)» определит максимальное значение из ячеек A1, A2, A3, A4 и A5.

4. MIN (МИН)

Функция MIN находит минимальное значение в заданном диапазоне ячеек. Например, формула «=MIN(A1:A5)» определит минимальное значение из ячеек A1, A2, A3, A4 и A5.

5. COUNT (СЧЁТ)

Функция COUNT подсчитывает количество числовых значений в заданном диапазоне ячеек. Например, формула «=COUNT(A1:A5)» подсчитает количество числовых значений в ячейках A1, A2, A3, A4 и A5.

6. IF (ЕСЛИ)

Функция IF выполняет условное вычисление в Excel. Она позволяет задать условие и выполнить определенные действия, в зависимости от выполнения условия. Например, формула «=IF(A1>10, «Больше 10», «Меньше или равно 10″)» проверит значение ячейки A1 и выведет «Больше 10», если оно больше 10, или «Меньше или равно 10», если оно меньше или равно 10.

7. CONCATENATE (СЦЕПИТЬ)

Функция CONCATENATE объединяет текстовые значения из нескольких ячеек в одну. Например, формула «=CONCATENATE(A1, » «, A2)» объединит значения из ячеек A1 и A2, добавив пробел между ними.

Это лишь небольшой обзор основных функций Excel. Программа располагает множеством других полезных функций, которые могут быть использованы для решения различных задач и выполнения операций с данными.

2.2. Создание и изменение формул массива

Для того чтобы правильно ввести формулу массива, нужно
выделить на листе область, размеры которой совпадают с ожидаемым
результатом.

Если выделить слишком большую область, то при вычислении
избыточные ячейки будут заполнены символами ошибки
#N/A. Если область вывода будет меньше, чем нужно, то часть
результатов пропадет. После выделения области, в
Formula Bar  записывается
формула и нажимается CTRL+SHIFT+ENTER.

Альтернативно, сначала можно ввести формулу в одну
ячейку, затем отметить область вывода, начиная с этой ячейки (право и
вниз), потом перейти в Formula Bar и нажать
CTRL+SHIFT+ENTER. 

Для того, чтобы изменить формулу массива нужно выделить
область содержащую результат. Затем нужно перейти
Formula Bar. При этом фигурные скобки вокруг формулы
{ } исчезнут. После этого формулу можно
изменить и нажать CTRL+SHIFT+ENTER.

Для того чтобы расширить область, которую занимает
формула массива, достаточно выделить для нее новую область, перейти в
Formula Bar и нажать CTRL+SHIFT+ENTER. А вот для того, чтобы уменьшить эту область
(например, чтобы избавиться от символов #N/A)
придется потратить больше сил. Сначала нужно встать на любую ячейку
области, перейти в Formula Bar и скопировать
строку формулы. Затем нужно стереть содержимое старой области и отметить
новую, меньшую область. После этого опять перейти в
Formula Bar, вставить формулу и нажать CTRL+SHIFT+ENTER.

Изменять отдельные ячейки в формуле массива нельзя. При
попытке сделать это появляется предупреждение .

Рис.27 Предупреждение о недопустимой операции с формулой массива

Функции для работы с матрицами в Excel

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).

Порядок применения формулы массива:

1. Выделить диапазон, где должен появиться результат действия формулы.
2. Ввести формулу (как и положено, со знака «=»).
3. Нажать сочетание кнопок Ctrl + Shift + Ввод.

В строке формул отобразится формула массива в фигурных скобках.

Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.

Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

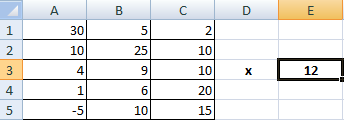
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Что такое матрица в Excel?

Матрица в Excel представляет собой таблицу, состоящую из ячеек, которые объединены по горизонтали и вертикали. Каждая ячейка может содержать данные, формулы или функции. Матрица обычно используется для организации и анализа больших объемов информации, таких как числовые данные, текст или даты.

В Excel матрица имеет свои адреса, которые обозначаются буквенно-цифровыми комбинациями. Адрес клетки матрицы состоит из буквы, обозначающей столбец, и номера строки. Например, клетка A1 находится на пересечении первого столбца и первой строки. При указании адреса матрицы выделяется прямоугольная область, где верхняя левая ячейка указывает первую ячейку, а нижняя правая ячейка указывает последнюю ячейку в матрице.

Матрицы в Excel можно использовать для различных операций, таких как сложение, вычитание, умножение и деление чисел. Каждая ячейка матрицы может содержать числовые значения, текстовые данные или формулы, которые автоматически обновляются при изменении данных в матрице.

Excel также предоставляет множество функций для работы с матрицами, таких как поиск суммы значений в столбце или строке, нахождение максимального или минимального значения в матрице, а также сортировка и фильтрация данных.

	A	B	C
1	10	20	=A1+B1
2	15	25	=A2+B2
3	30	40	=A3+B3

В приведенном выше примере мы имеем матрицу размером 3×3, где в каждой ячейке находится число или формула. Например, в ячейке C1 находится формула, которая суммирует значения из ячеек A1 и B1. При изменении значений в ячейках A1 и B1 формула автоматически обновится и пересчитает значение в ячейке C1.

Матричные шаблоны Excel

Иногда очень сложно выполнить шаги по созданию матрицы в Excel или в EdrawMax Online и создать идеальную диаграмму. В настоящее время есть примеры матриц из галереи шаблонов EdrawMax, которые вы можете редактировать немедленно или для получения дополнительных ссылок. Примеры матриц не только помогают глубже понять матрицу и ее классификацию, но и помогают рисовать матрицы без усилий.

Шаблон матрицы Excel

Характер человека состоит из всех качеств, которые отличают его от других. Человек с хорошим характером думает, чувствует и действует в соответствии с некоторыми общепринятыми чертами. Есть несколько черт характера, таких как упорство, любопытство, самообладание, социальный интеллект, энтузиазм, оптимизм и благодарность.

Онлайн-шаблон матрицы

Это базовая модель матрицы Ансоффа с друзьями в сообществе! Цель этой матрицы Ансоффа — помочь компаниям планировать и выбирать свои продукты и стратегии роста рынка.

Шаблон матрицы

Матричная диаграмма — это инструмент управления проектом, с помощью которого можно сравнивать и определять отношения между различными наборами данных. Это графические наборы данных, которые упрощают сложные отношения между программами и функциями.

Форматирование матрицы

После того, как вы создали матрицу в программе Excel, вы можете ее форматировать, чтобы сделать ее более удобной для чтения и анализа. Вот некоторые способы форматирования матрицы:

• Изменение ширины и высоты ячеек: вы можете изменить размер ячеек матрицы, чтобы сделать ее более компактной или скомпонованной. Для этого выделите нужные ячейки, перейдите во вкладку «Макет» на ленте инструментов и используйте опции «Ширина столбца» и «Высота строки».
• Применение условного форматирования: вы можете установить определенные условия для ячеек матрицы и изменить их форматирование в зависимости от выполнения условия. Например, вы можете выделить все ячейки, содержащие значения больше определенного числа, красным цветом. Для этого перейдите на вкладку «Главная» на ленте инструментов, выберите опцию «Условное форматирование» и следуйте инструкциям.
• Добавление границ и заливки: вы можете добавить линии границ и задать цвет заливки ячеек матрицы. Это может помочь вам лучше отличить разные части матрицы или обозначить важные значения. Для этого выделите нужные ячейки, перейдите на вкладку «Главная» и используйте опции «Границы» и «Заливка».
• Применение числового форматирования: если ваша матрица содержит числовые данные, вы можете применить различные числовые форматы, чтобы отобразить данные в нужном виде. Например, вы можете отображать числа с определенным числом знаков после запятой или в процентном формате. Для этого выберите нужные ячейки, перейдите на вкладку «Главная» и выберите нужный формат числа в опции «Числовое форматирование».
• Применение шрифтов и цветов: вы можете изменить шрифт и цвет текста в ячейках матрицы, чтобы добавить акцент или создать определенное настроение. Для этого выделите нужные ячейки, перейдите на вкладку «Главная» и используйте опции «Шрифт» и «Цвет шрифта».

Вычисление обратной матрицы в MS EXCEL

Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE.

• Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
• СОВЕТ: О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
• Матрица А-1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А-1*А=Е и А*А-1=Е, где Е единичная матрица порядка n.
• Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР().

Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9, то для получения транспонированной матрицы нужно (см. файл примера):

• выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А8:В9, например, Е8:F9
• в Cтроке формул ввести формулу =МОБР(A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)

Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.

Массив может быть задан не только как интервал ячеек, например A8:B9, но и как массив констант, например =МОБР({5;4: 3;2}).

Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией.

Ссылка на массив также может быть указана как ссылка на именованный диапазон.

Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.

Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ()), а как ошибочное значение.

Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений

СОВЕТ: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР().

В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.

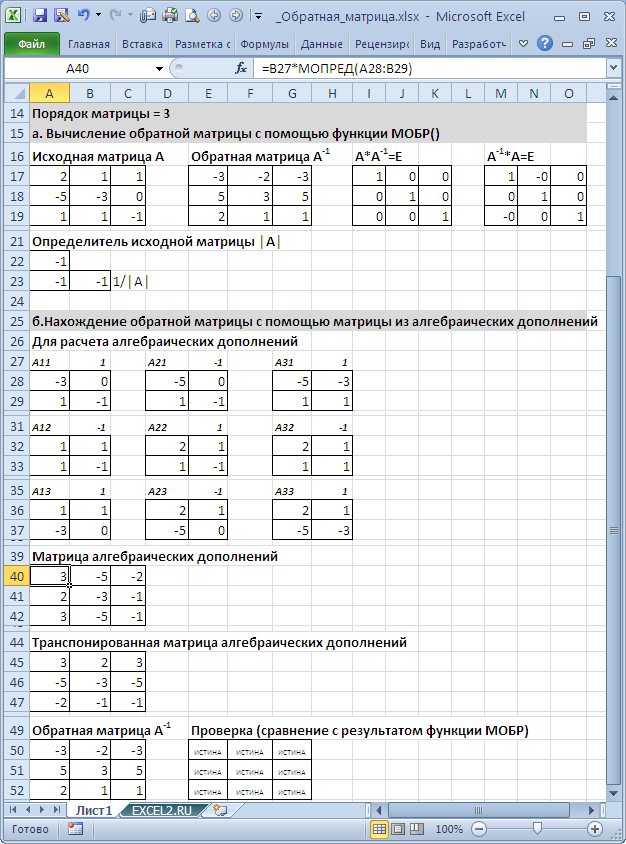
В качестве проверки можно перемножить исходную и обратную матрицы. В результате должна получиться единичная матрица.

Как рассчитать весовые коэффициенты для матрицы БКГ в Excel

Для расчета весовых коэффициентов для матрицы БКГ в Excel следуйте этим шагам:

Создайте таблицу в Excel, в которой каждый фактор будет представлен в отдельном столбце, а все альтернативные варианты решений — в строках

В первом столбце можно указать названия факторов, а в первой строке — названия альтернативных вариантов решений.
Проанализируйте каждый фактор и присвойте ему важность на основе шкалы от 1 до 5, где 1 — наименее важный фактор, а 5 — наиболее важный фактор. Запишите эти значения в соответствующие ячейки таблицы.
Последовательно пройдитесь по каждому столбцу таблицы и приведите значения в столбцах к относительным весам

Для этого выполните следующие действия:

• Найдите сумму значений в каждом столбце.
• Поделите каждое значение на сумму всех значений в столбце, чтобы получить относительный вес каждого фактора.

Запишите рассчитанные относительные веса в отдельный столбец справа от таблицы.
Суммируйте все значения относительных весов и убедитесь, что их сумма равна 1. Если сумма не равна 1, проверьте правильность процедуры расчета.

После выполнения этих шагов, вы будете иметь готовые весовые коэффициенты для матрицы БКГ. Их можно использовать для оценки альтернативных вариантов решений и принятия обоснованных решений на основе анализа данных.

Матрица БКГ

Матрица Бостонской консалтинговой группы (БКГ) — основа анализа продвижения групп товаров, которая базируется на темпе роста рынка и на их доле в конкретном рыночном сегменте.

Согласно стратегии матрицы, все товары разделены на четыре типа:

«Собаки» — это товары, имеющие малую долю рынка в сегменте с низким темпом роста. Как правило, их развитие считается нецелесообразным. Они являются неперспективными, их производство следует сворачивать.

«Трудные дети» — товары, занимающие малую долю рынка, но на быстро развивающемся сегменте. Данная группа имеет также ещё одно название — «тёмные лошадки». Это связано с тем, что у них имеется перспектива потенциального развития, но в то же время они требуют для своего развития постоянных денежных вложений.

«Дойные коровы» — это товары, занимающие значительную долю слабо растущего рынка. Они приносят постоянный стабильный доход, который компания может направлять на развитие «Трудных детей» и «Звезд». Сами «Дойные коровы» вложений уже не требуют.

«Звёзды» — это наиболее успешная группа, занимающая существенную долю на быстрорастущем рынке. Эти товары уже в настоящее время приносят значительный доход, но вложения в них позволят этот доход ещё больше увеличить.

Задачей матрицы БКГ является определение того, к какой из данных четырех групп можно отнести конкретный вид товара для того, чтобы проработать стратегию его дальнейшего развития.

3.5. Надстройки

Написанные пользователем программы хранятся в той книге
Excel, в которой они были созданы, в ее специальных разделах, называемых
модулями. Для того чтобы эти макросы были доступны в других
книгах, их можно туда скопировать, но можно поступить и по-другому –
создать надстройку.

Надстройка – это специальный файл Excel,
содержащий в  себе несколько VBA модулей, связанных со всеми
необходимыми библиотеками DLL. Надстройку можно подключить к системе
Excel для расширения ее возможностей.

Стандартная версия Excel включает несколько надстроек,
среди которых для нас примечательны две: Solver Add-In и Analysis
Toolpak.

Надстройка

Solver Add-In предназначена для оптимизации значения в целевой
ячейке. Решение находится с помощью поиска величин в других ячейках,
функционально связанных с целевой.

Надстройка

Analysis Toolpak содержит набор статистических инструментов
для анализа данных

В сети можно найти много надстроек для Excel, некоторые
из которых распространяются свободно, другие за деньги. Вот некоторые
примечательные.

J-Walk Chart Tools Add-In – бесплатная утилита для
управление диаграммами: добавление подписей, ярлыков, и т.п. – все то,
что отсутствует в стандартной версии.

XLStat
– большой (и дорогой) пакет статистического анализа, включающий, в
частности, и PLS регрессию.

Multivariate Analysis Add-in – условно бесплатный пакет для
анализа многомерных данных, созданный в Бристольском университете

Fitter – надстройка для нелинейного регрессионного анализа.

Chemometrics – пакет функций листа, выполняющий анализ
многомерных данных.

Подробнее о надстройках можно прочитать

здесь. 

Формулы массива

построение массива с помощью Excel в большинстве случаев требует использования формулы массива. Основное их отличие в том, что результатом является не одиночное значение, а массив данных (массив чисел).

Чтобы использовать формулу массива:

1. Выберите область, в которой будет отображаться результат формулы.
2. Введите формулу (как и положено, со знаком «=» и «=»).
3. Нажмите комбинацию клавиш Ctrl+Shift+Enter.

В строке формул формула массива отображается в фигурных скобках.

Чтобы изменить или удалить формулу массива, выберите весь диапазон и выполните соответствующие действия. Та же комбинация (Ctrl+Shift+Enter) используется для внесения изменений. Часть матрицы изменить нельзя.

Как найти обратную матрицу в Excel?

В отличие от транспонированной матрицы, вычислить обратную матрицу технически несколько сложнее. Посчитать обратную матрицу можно через построение матриц алгебраических дополнений и определителя исходной матрицы. Однако сложность вычисления по данному алгоритму имеет квадратичную зависимость от порядка матрицы. К примеру, для обращения квадратной матрицы 3-го порядка нам необходимо будет дополнительно сделать 9 матриц алгебраических дополнений, транспонировать итоговую созданную матрицу и поэлементно разделить на определитель начальной матрицы, что затрудняет возможность подобного расчета в Excel. Поэтому воспользуемся стандартной функцией МОБР, которая позволит найти обратную матрицу:

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

Что можно делать с матрицами

В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.

Транспонирование

Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием. 

Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.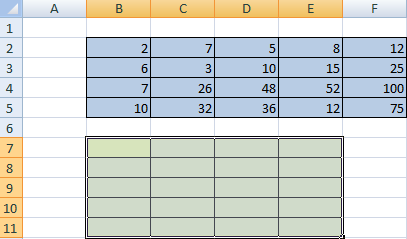

Далее есть несколько методов, как можно осуществить транспонирование. 

Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».

Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.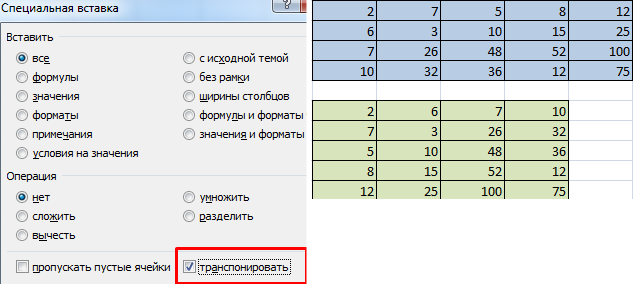

Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.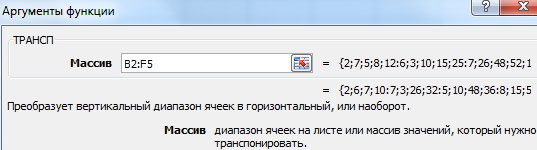

После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:

1. Выделить набор ячеек, отведенных под транспонированную матрицу.
2. Нажать клавишу F2.
3. Нажать на горячие клавиши Ctrl + Shift + Enter.

Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.

Видеоурок

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя стало известно автору, войдите на сайт как пользователь и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?Оставьте комментарий

Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст

Что учитывать при выборе бизнес идеи?

Выбирая бизнес идею, необходимо учитывать следующие факторы.

Современность товаров или услуг, способов их продажи

Некоторые идеи становятся устаревшими уже по истечению нескольких лет. Например, нанимать
коммивояжеров, чтобы они напрямую распространяли товары, еще пару лет назад было выгодной идеей,
особенно, если такой продукции не могли предложить конкуренты. Но сейчас с большой долей
вероятности такой бизнес потерпит катастрофу.

Наличие постоянной клиентской аудитории

Разумно выбрать такую идею, которая охватывала бы максимально широкий круг населения, или
наоборот, максимально специфический, требующий уникальных услуг. К примеру, открывать барбершоп стоит, если город довольно большой, и есть
достаточно людей, постоянно пользующихся услугами. Если нет уверенности, что клиентов будет
достаточно, лучше открыть обычную парикмахерскую.

Отсутствие прямых конкурентов

При наличии, например, супермаркета по соседству лучше не открывать маленький продуктовый
магазин – большинство решит пойти в привычное место.

Высокое качество предлагаемых товаров или услуг

Задача рекламы и маркетинга – привлечь покупателя. Удержать его сможет лишь качество
предлагаемой продукции или услуг.

Используйте функции для работы с матрицей

Excel предоставляет множество функций, которые можно использовать для работы с матрицами. Вот некоторые из них:

• Матричные формулы: с помощью этих формул можно выполнять операции со всей матрицей или с ее частью. Например, суммировать все элементы матрицы или умножить матрицу на число.
• Функции массива: такие функции могут работать с массивами значений и возвращать результат как массив. Например, можно использовать функцию СРЗНАЧ для нахождения среднего значения для каждого столбца матрицы.
• Функции работы с данными: Excel имеет функции для сортировки, фильтрации и анализа данных в матрице. Например, можно использовать функцию СОРТИРОВАТЬ для сортировки матрицы по определенному столбцу.

Вот некоторые примеры использования функций для работы с матрицей:

1. Чтобы использовать матричную формулу, нужно выделить диапазон ячеек, в которых будет содержаться результат, ввести формулу и закрыть ее фигурной скобкой. Например, для сложения двух матриц можно использовать формулу =A1:A3+B1:B3.
2. Чтобы использовать функцию массива, нужно выделить диапазон ячеек, в которых будет содержаться результат, ввести формулу и нажать комбинацию клавиш Ctrl + Shift + Enter, чтобы ввести ее как массивную формулу. Например, для нахождения среднего значения для каждого столбца матрицы можно использовать формулу =СРЗНАЧ(A1:C1:A3:C3).
3. Чтобы использовать функцию работы с данными, нужно ввести формулу и указать диапазон данных, к которому она будет применяться. Например, чтобы отфильтровать матрицу по определенным критериям, можно использовать формулу =ФИЛЬТР(A1:C3,A1:C3>10).

Использование функций для работы с матрицей поможет вам выполнять сложные операции с данными и получать нужные результаты быстро и эффективно.