Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
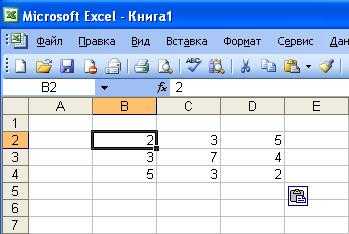
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
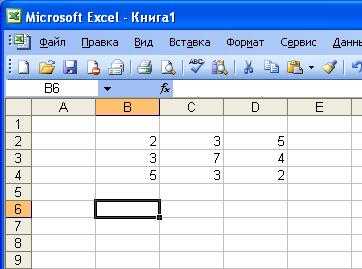
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
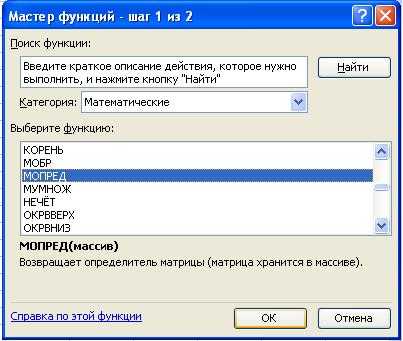
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .

Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).

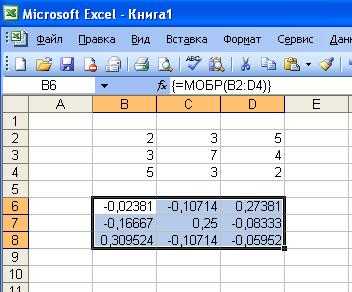
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
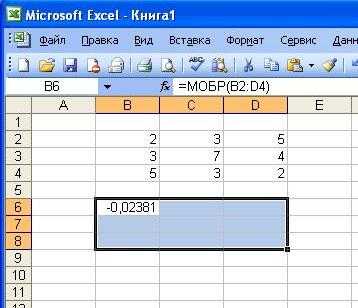

Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.
Данную систему уравнений можно представить в матричной форме:
Матрица неизвестных вычисляется по формуле
где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Как воспользоваться функциями подбора параметра и поиска решения в Excel
Функция поиска решения понадобится по мере необходимости найти неведомую величину
Табличный микропроцессор Microsoft Excel может делать не только лишь обыкновенные операции с числами (сложение, умножение), расчет суммы либо среднего значения. У данной нам программки имеется весьма мощнейший функционал, который дозволяет решать задачки разной трудности. К примеру, Эксель может улучшить значения в таблице, подставляя их таковым образом, чтоб они удовлетворяли определенным аспектам. Для этого программка вооружена особыми средствами для анализа данных: 1-ый — это подбор параметра, а 2-ой — поиск решения.
Методы решения задач
1. Методы дифференциального исчисления
Данный метод основан на использовании производных функций, которые определяют ее поведение в заданной точке. Метод дифференциального исчисления позволяет найти экстремумы функции. Для этого необходимо вычислить производную функции и найти точки, где она равна нулю. После этого можно сравнить значения функции в этих точках и выбрать ту, где достигается экстремум.
2. Методы градиентного спуска
Методы градиентного спуска также используют производные функций, но вместо поиска точек, где они равны нулю, ищут точки минимума или максимума функции. Идея методов градиентного спуска заключается в том, чтобы начать с некоторой точки и постепенно двигаться в направлении, противоположном градиенту функции, чтобы достичь минимума или максимума.
3. Методы динамического программирования
Методы динамического программирования применяются в случаях, когда задача может быть разбита на подзадачи, которые можно решить независимо друг от друга. Идея заключается в том, чтобы решить каждую подзадачу только один раз и сохранить полученные результаты для использования в последующих подзадачах. Это позволяет значительно сократить время решения задачи.
4. Методы комбинаторной оптимизации
Методы комбинаторной оптимизации применяются в задачах, связанных с выбором наилучшей комбинации из заданного набора альтернатив. Такие задачи могут быть решены перебором всех возможных комбинаций, однако это затратно по времени. Вместо этого, применяются эвристические алгоритмы, которые позволяют приближенно найти оптимальное решение.
5. Методы линейного программирования
Методы линейного программирования применяются в задачах оптимизации при наличии линейных ограничений. Данный метод основан на геометрическом представлении задачи и нахождении точек пересечения линейных функций, ограничивающих решение. Метод линейного программирования позволяет найти точку максимума или минимума линейной функции при заданных линейных ограничениях.
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Простой пример использования Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см. файл примера ).
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.
При ограничении 17 м3 Поиск решения найдет решение.
Решить уравнения в Excel
Solver Add-in мощный и полезный инструмент Excel, который выполняет вычисления, чтобы дать оптимальные решения, отвечающие указанным критериям. Итак, давайте посмотрим, как использовать надстройку Solver для Excel. Надстройка Solver не загружена в excel по умолчанию, и нам нужно загрузить ее следующим образом:
Откройте Excel и нажмите кнопку «Файл» или «Офис», затем нажмите « Параметры Excel.
Откроется диалоговое окно «Параметры Excel» и нажмите Надстроек с левой стороны. Затем выберите Надстройка Solver из списка и нажмите «Идти» кнопка.
В диалоговом окне надстроек отображается список надстроек. Выберите надстройку Solver и нажмите кнопку «Ok».
Теперь надстройка Solidver добавлена в лист Excel. Нажмите на вкладку «Данные» и в крайнем правом углу вы увидите добавленную надстройку Solver.
Как использовать надстройку Solver
Мы добавили надстройку Solver в Excel, и теперь мы увидим, как ее использовать. Чтобы понять это лучше, давайте рассмотрим пример расчета прибыли продукта. См. Таблицу Excel ниже с некоторыми примерами данных. Чтобы найти прибыль%, воспользуемся формулой прибыль% = ((Цена продажи-Себестоимость) / Себестоимость) * 100
Мы можем видеть, что есть три продукта: Продукт А, Продукт Б и Продукт С с ценой, продажей и прибылью (%) соответствующих продуктов. Теперь наша цель — получить прибыль (%) продукта А до 20%. Нам нужно узнать стоимость цены и продажные цены продукта A, необходимые для получения прибыли как 20%. Здесь мы также имеем ограничение, согласно которому стоимость цены должна быть больше или равна 16 000, а цена продажи должна быть меньше или равна 22 000. Итак, сначала нам нужно перечислить нижеследующую информацию, основанную на примере, который мы взяли.
Целевая ячейка: B5 (Прибыль%)
Переменные ячейки для продукта A: B3 (себестоимость) и B4 (цена продажи)
Ограничения: B3> = 16 000 и B4 <= 22 000
Формула, используемая для расчета прибыли%: ((Цена продажи-Себестоимость) / Себестоимость) * 100
Целевое значение: 20
Поместите формулу в целевую ячейку (B5) для расчета прибыли%.
Это необходимая информация, необходимая для решения любого уравнения с помощью надстройки Solver в Excel.
Теперь запустите надстройку Solver, щелкнув вкладку «Данные» и выберите «Solver».
ШАГ 1: Укажите «Целевую ячейку» как B5, «Значение» в качестве целевой прибыли% как 20 и указать ячейки, которые необходимо изменить для удовлетворения требуемой прибыли%. В нашем случае, B3 (C.P) а также B4 (S.P) необходимо указать как $ B $ 3: $ B $ 4 в разделе «Изменение переменных ячеек».
ШАГ 2: Теперь пришло время добавить ограничения. В нашем случае цена себестоимости (B3)> = 16 000 и цена продажи (B4) <= 22 000. Нажмите кнопку «Добавить» и добавьте ограничения следующим образом.
ШАГ 3: После ввода всех необходимых данных нажмите кнопку «Решить». Он спрашивает, хотите ли вы сохранить решение решателя вместе с некоторыми вариантами. Выберите на основе вашего требования и нажмите кнопку «ОК».
Теперь вы увидите, что последняя цена себестоимости и продажная цена была изменена на 17, 708 и 21, 250 соответственно, чтобы получить 20% прибыли.
Это способ использовать надстройку Solver для решения уравнений в Excel. Исследуйте это, и вы можете получить больше от него. Поделитесь с нами, как наилучшим образом вы использовали надстройку Solver.
Похожие сообщения:
- Как вставить таблицу Excel в документе Word
- Лучше всего использовать поле «Имя» в Excel
- Сравнение таблиц Excel с помощью Excel Compare Tool
- Как создать пользовательские функции Excel
- История и эволюция программного обеспечения Microsoft Office
Tweet
Share
Link
Plus
Send
Send
Pin
Оптимизация графика работ по проекту с помощью Поиска решений в EXCEL
Решим задачу об оптимизации плана-графика работ по проекту с помощью Поиска решений MS EXCEL 2010. В качестве примера разберем задачу из сборника «Методы оптимизации управления и принятия решений» авторы Зайцев М.Г. и Варюхин С.Е. (2008г.). Задача 3.7 «Проект комапании Мегашоп».
Сборник задач «Методы оптимизации управления и принятия решений» довольно популярен в качестве задачника для Вузов, поэтому ссылки на него встречаются повсеместно в интернете. Приятно, что для каждой задачи имеется ответ в конце книги — можно сравнить получившееся решение с решением, которое найдено авторами с помощью Поиска решения (в году так 2000-м, я полагаю).
Функция «Подбор параметра»
Подбор параметра в Excel дозволяет подобрать некий определенный параметр, значение которого непонятно. Чтоб было понятней, можно привести таковой пример. Допустим, есть прямоугольник со сторонами A и B. Понятно, что общая площадь данной нам фигуры составляет 400 квадратных метров, а сторона B — 40 метров. Сторона A неведома и, соответственно, необходимо ее отыскать. Для решения таковой задачки нужно заполнить рабочий лист программки теми данными, которые уже известны. Для этого необходимо сделать таблицу с 2 колонками и 3 строчками (спектр ячеек A1:B3).
1-ый столбец будет содержать заглавие сторон прямоугольника и буковку, обозначающую его площадь (т.е. A, B и S). А во 2-м столбце нужно указать известные значения:
- в примыкающей ячейке для стороны B (ячейка B2) написать — 40 (значение для стороны А остается пустым);
- а в примыкающем поле для площади прямоугольника (поле B3) написать последующую формулу: = B1*B2 (т.е. формула для расчета площади).
Если все было изготовлено верно, то в поле B3 обязано быть значение 0. Потом нужно выделить эту ячейку и избрать в панели меню пункты: «Сервис — Подбор параметра». В показавшемся окне необходимо указать то значение, которое обязано быть получено в итоге, т.е. 400. В строке «Установить в ячейке» будет обозначено поле «B3»: поменять его не надо, так и обязано быть (сюда будет выведен итог). А в строке «Изменяя значение» нужно избрать неведомый параметр, т.е. поле B1. Опосля нажатия клавиши «ОК» программка выдаст итог: сторона А — 10 метров, а в поле общей площади прямоугольника будет обозначено число 400.
Это была весьма обычная задачка на уровне 3 класса, но при помощи таковой функции можно решать и наиболее сложные задачки. К примеру, вы решили приобрести для себя кар в кредит. Вы буквально понимаете, что можете выплачивать каждомесячную выплату в размере 1000 $ (но не больше), также, что банк выдает автокредит с процентной ставкой 6,5%. Сущность задачки заключается в последующем: «Какова наибольшая сумма машинки, которую можно взять в кредит на таковых критериях?». Другими словами сейчас программка будет находить стоимость кара, отталкиваясь от того, что каждомесячный платеж не должен превосходить 1000 $. Таковой пример является уже наиболее сложным, также наиболее удобным, нежели расчет площади прямоугольника.
Запуск инструмента Поиск решения
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
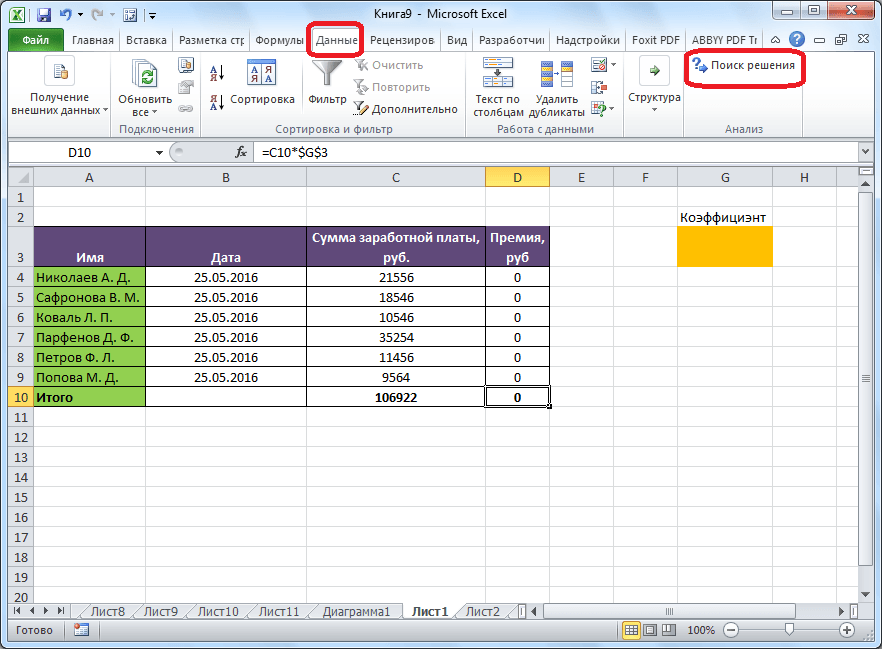
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
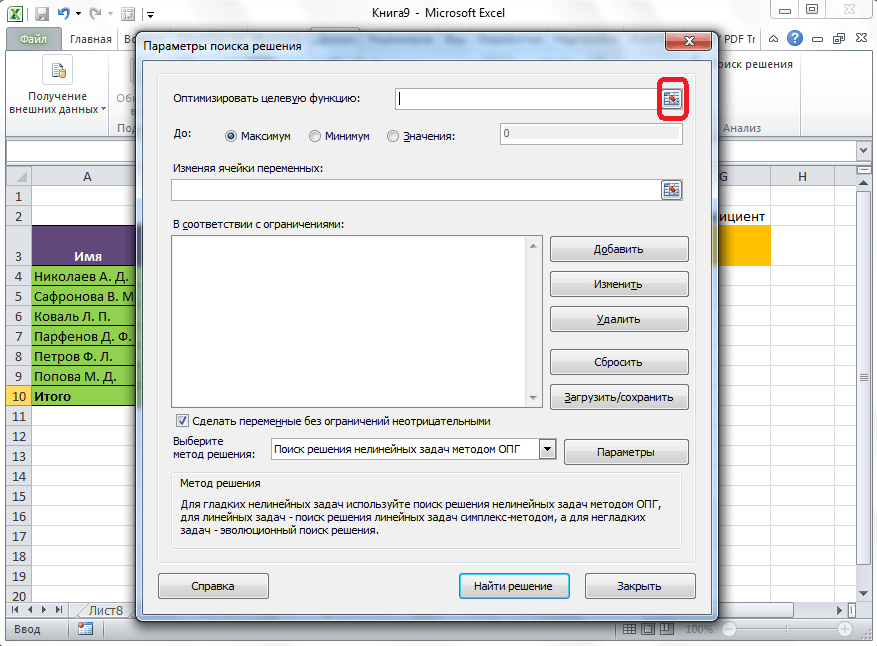
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
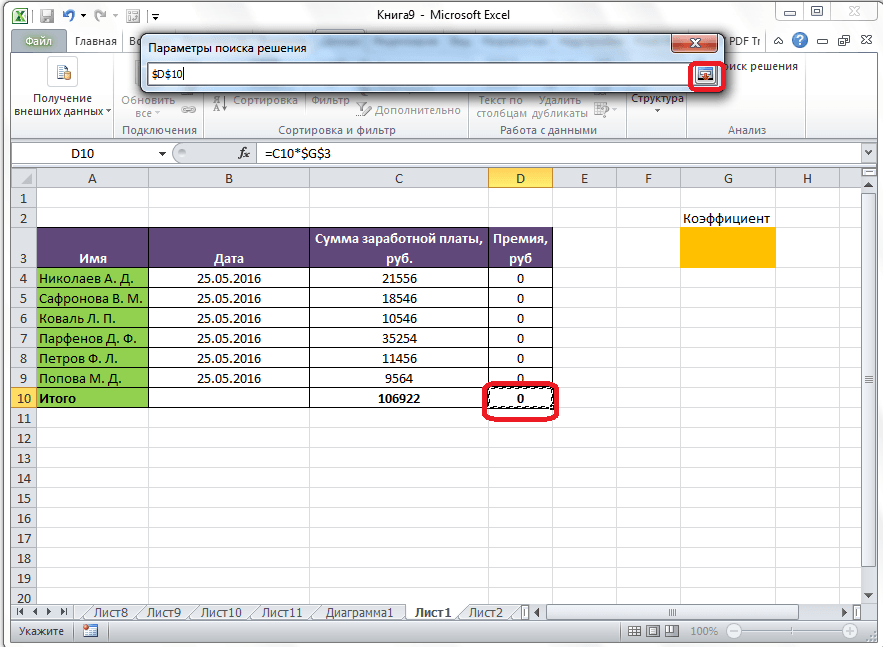
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
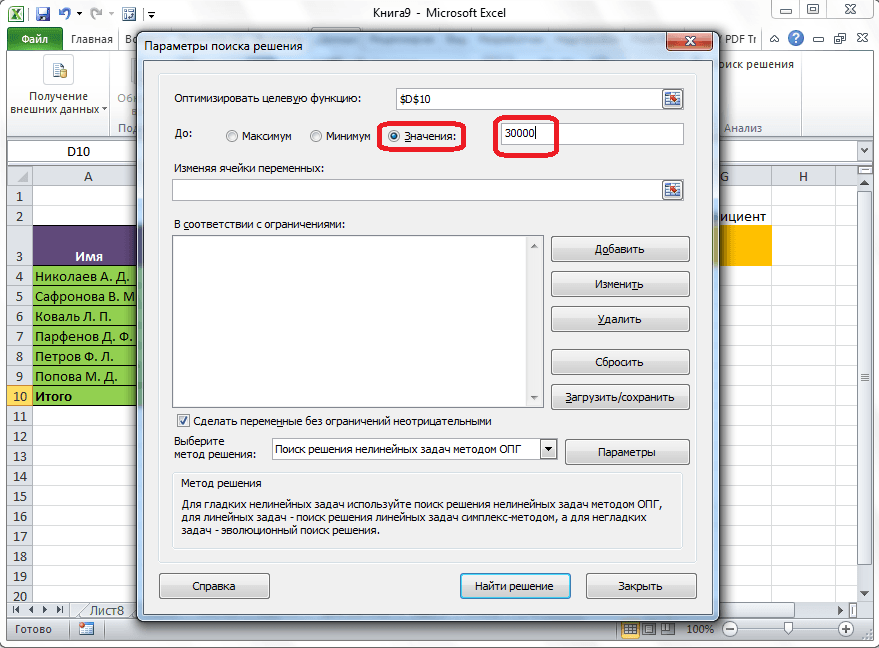
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
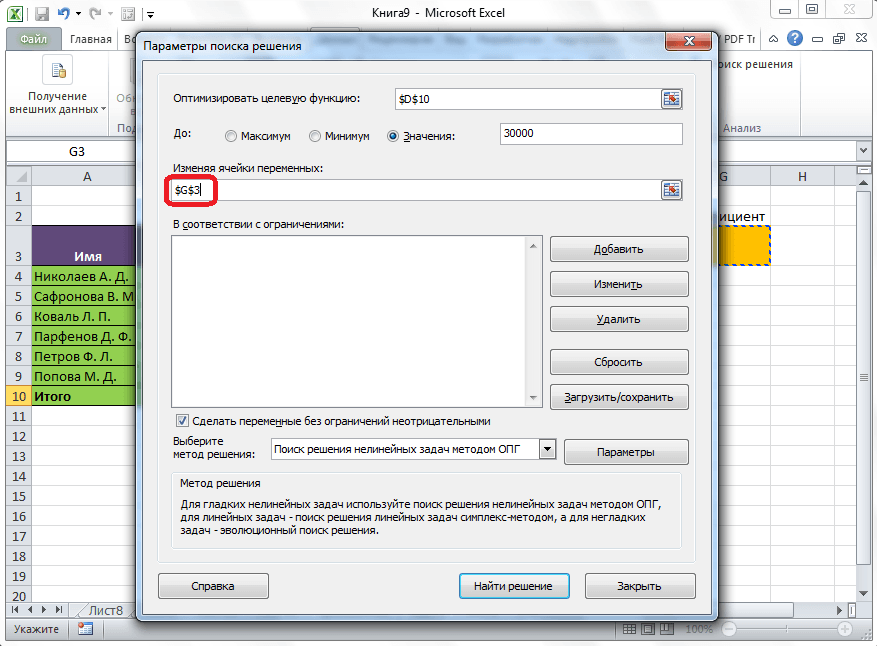
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
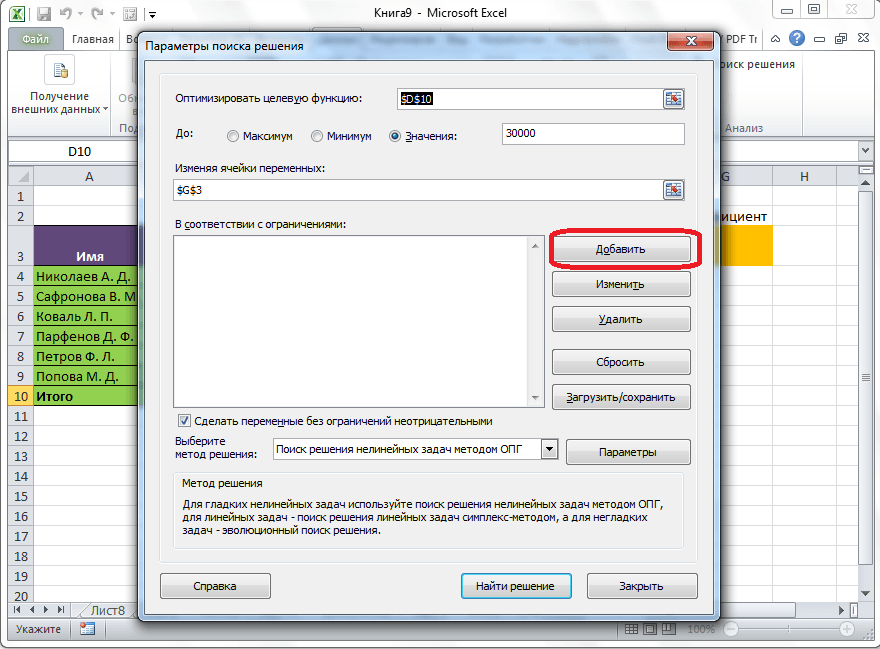
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
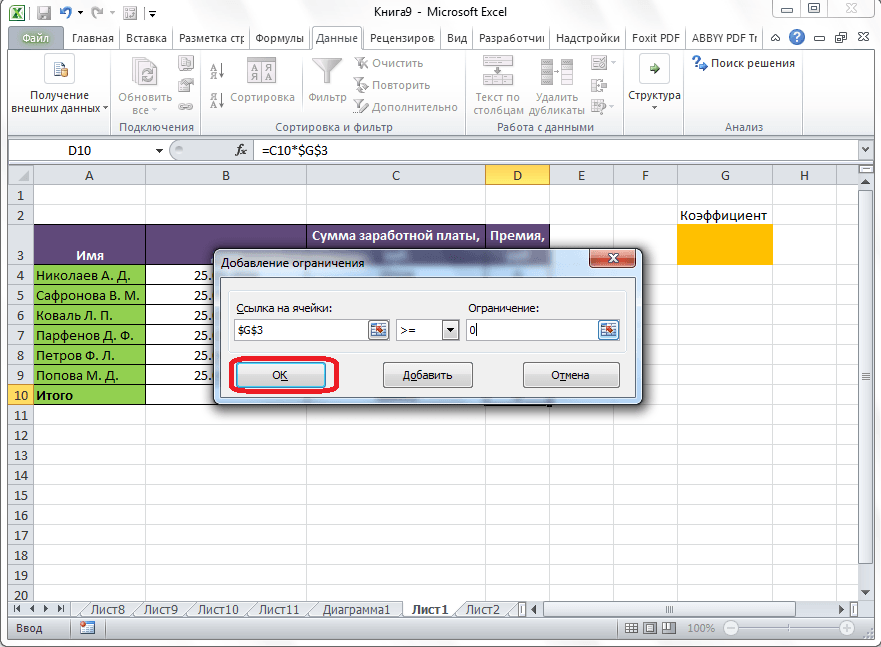
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
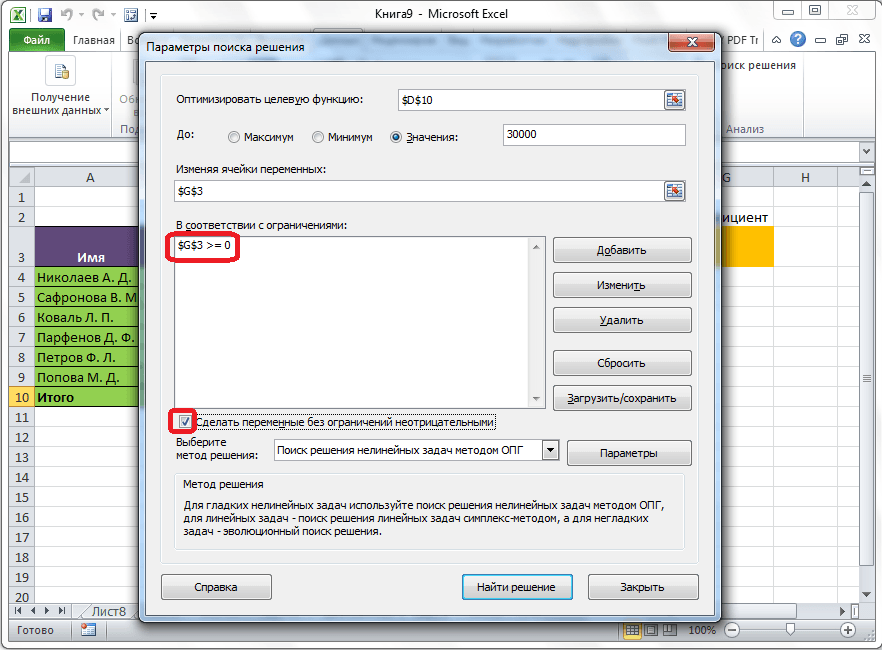
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
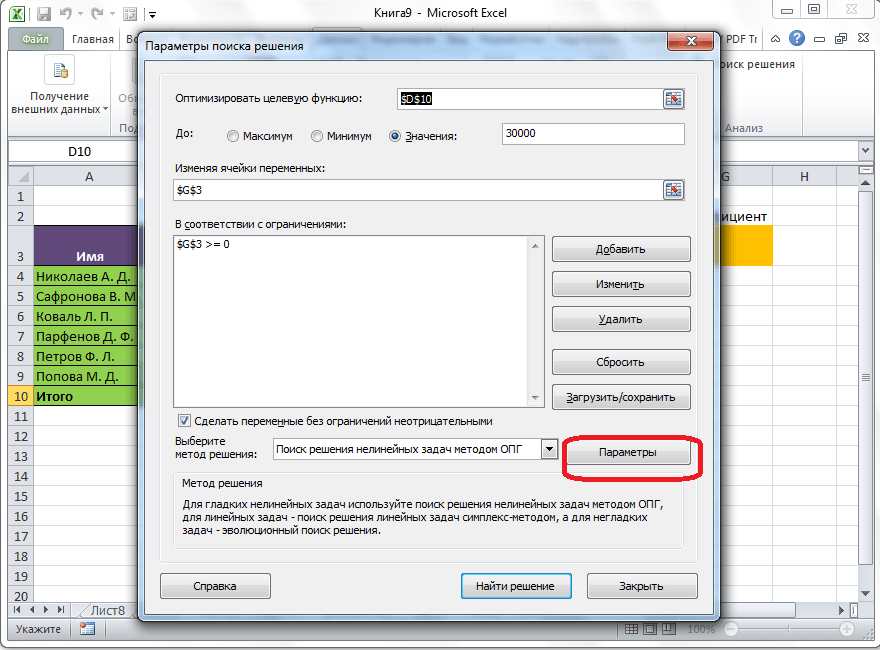
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
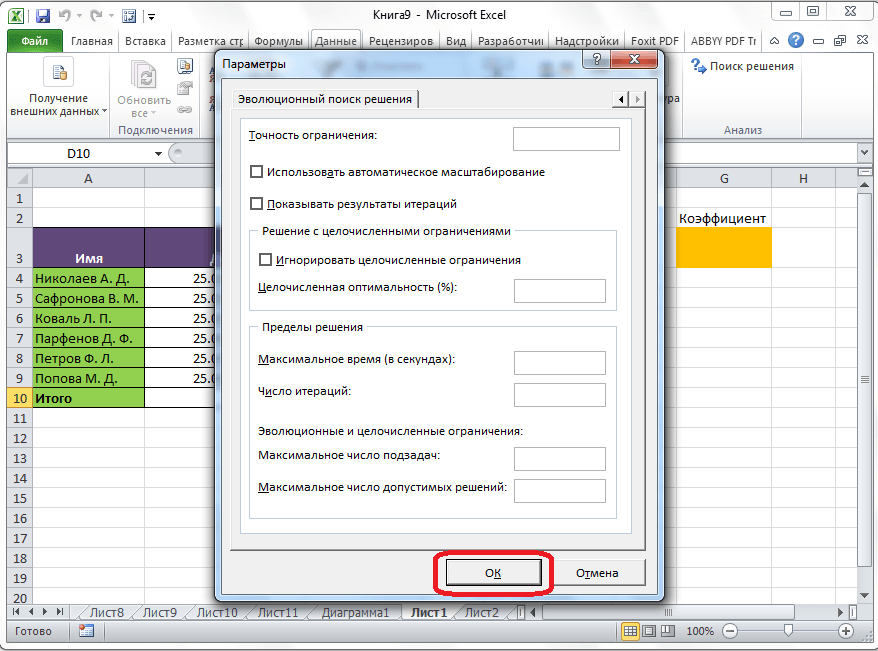
После того, как все настройки установлены, жмем на кнопку «Найти решение».
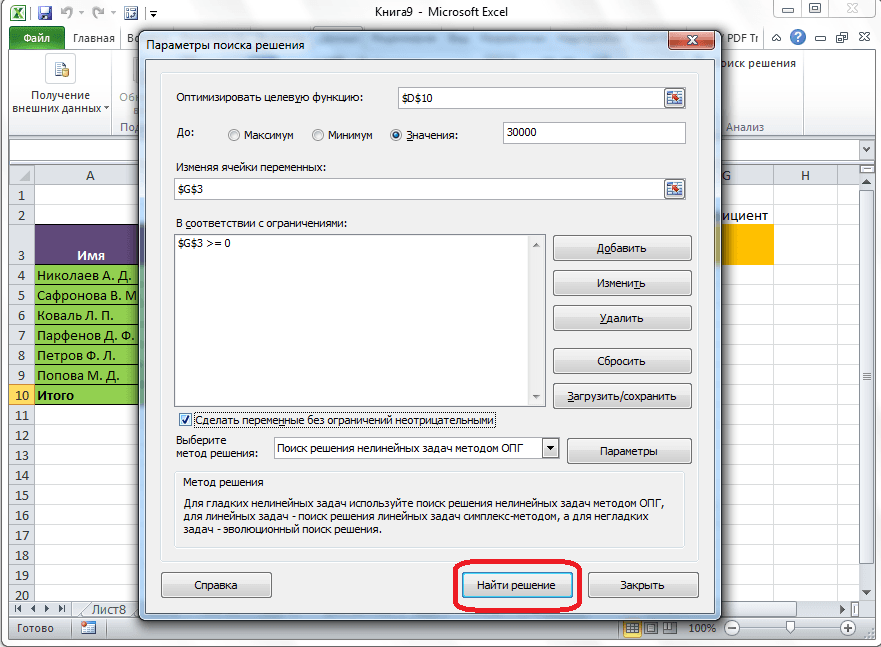
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
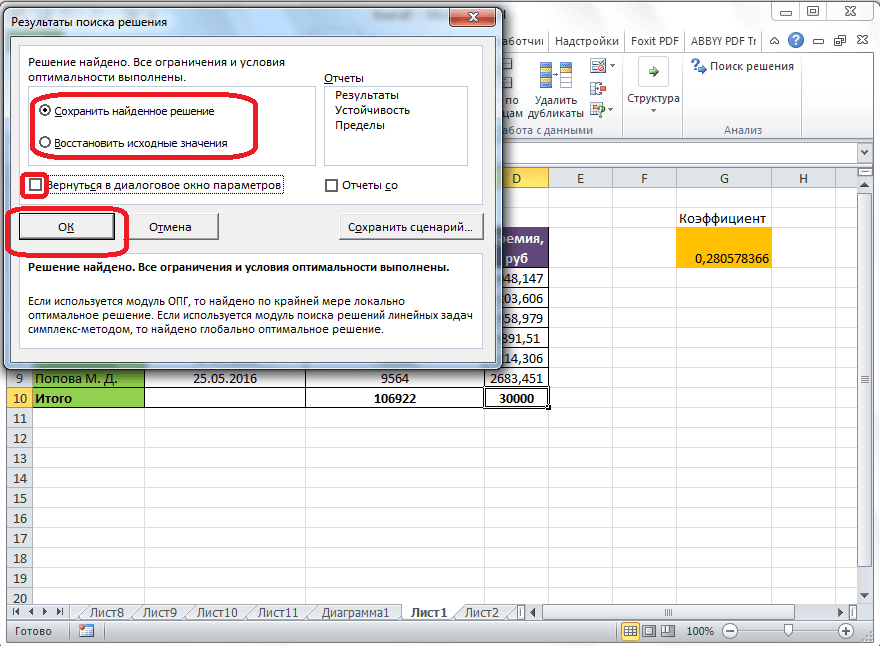
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
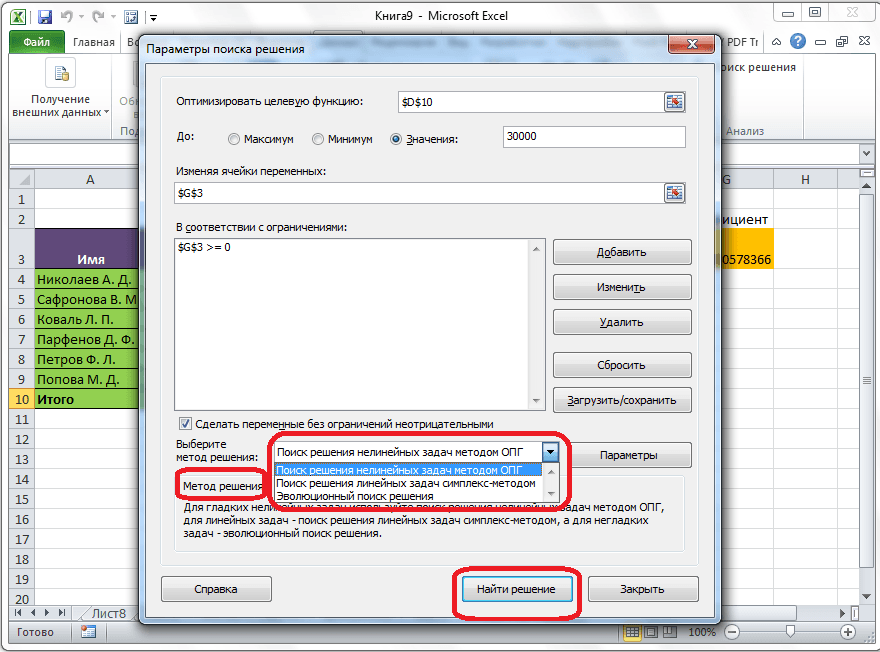
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию , но в то же время, имеет и существенные различия с ним.
Поиск оптимального решения в Excel
Решение задач оптимизации в Excel чаще всего осуществляется именно с помощью надстройки «Поиск решения».Например, с помощью этой функции можно решить транспортную задачу. Как известно, главной целью транспортной задачи является расчет оптимального маршрута, чтобы затраты на перевозки груза при этом были минимальными. В таких задачах имеется уже не один, а одновременно несколько значений, которые нужно рассчитывать. Как правило, обычно известно лишь количество фирм, количество поставщиков, общие запасы товара и потребность каждой фирмы в этом товаре (кому сколько нужно). И нужно рассчитать, как весь этот груз развести, чтобы стоимость перевозок была минимальной.
Процедура поиска оптимального значения в Excel осуществляется не так уж и просто, но принцип примерно тот же, что и в первом случае: пользователь указывает диапазон изменяемых ячеек и поле, куда выводить итоговый результат, а все остальное программа сделает сама. Вот такими способами осуществляется решение задач оптимизации в табличном процессоре Microsoft Excel.
Проблемы решения нелинейных задач в Excel
Во-первых, Excel предназначен в первую очередь для работы с линейными моделями, поэтому решение нелинейных задач в нем может быть затруднительным. Например, вычисление градиента для оптимизации может требовать использования сложных формул и макросов, что может быть неприятным и трудоемким.
Во-вторых, Excel имеет ограниченные возможности для работы с математическими функциями высокого порядка, такими как синус, косинус, экспонента и другие. Это может сильно ограничить способность решения нелинейных задач в Excel и требовать от пользователя постоянного использования аппроксимаций и приближенных методов.
И, наконец, Excel может иметь ограничения на количество итераций или точность вычислений при решении нелинейных задач. Такие ограничения могут привести к неправильным результатам или сбоям в процессе решения задачи.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Лабораторная работа №12: Нахождение решения задач нелинейного программирования (метод множителей Лагранжа)
Научиться решать задачи нелинейного программирования.
Рекомендации по решению:
1. При решении задач нелинейного программирования средствами Microsoft Excel используется надстройка Поиск решения, которая позволяет найти оптимальные решения.
2. При решении задач линейного программирования средствами MathCad с помощью встроенной функции Maximize (в случае поиска максимума функции) или Minimize (в случае поиска минимума функции).
Задание к лабораторной работе:
Составить математическую модель задачи. Для расчёта модели использовать метод множителей Лагранжа.
Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов. При продаже х кг муки через магазин расходы на реализацию составляют
2
Решение. Составим математическую модель задачи. Найдем минимум суммарных расходов
Для расчета модели используем метод множителей Лагранжа. Составим функцию Лагранжа.
Найдем частные производные функции F по х1, х2 и λ, приравняем к нулю, получим систему уравнений:
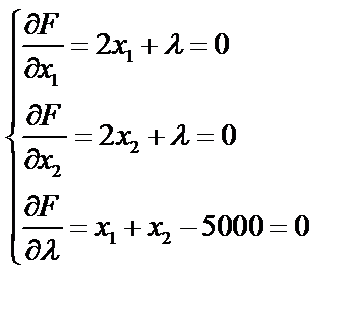
Из первого и второго уравнений имеем x1 – x2 =0.
Решая это уравнение совместно с третьим, имеем λ = -5000, х1 = 2500, х2 = 2500, L=12 500 тыс. ден. ед. Давая х1 значения больше и меньше 2500 находим L и из определения экстремума функции получаем, что L при х1 = х2 = 2500 достигает минимума.
Ответ. Для получения минимальных расходов необходимо расходовать в сутки через магазин и торговых агентов по 2500 кг муки, при этом расходы на реализацию составят 12 500 тыс. ден. ед.
| Переменные: | x1 | x2 | Значение ЦФ |
| Значения переменных | |||
| Коэффициенты Ц.Ф. | Значения огр-ний | ||
| Коэффициенты ограничений: |
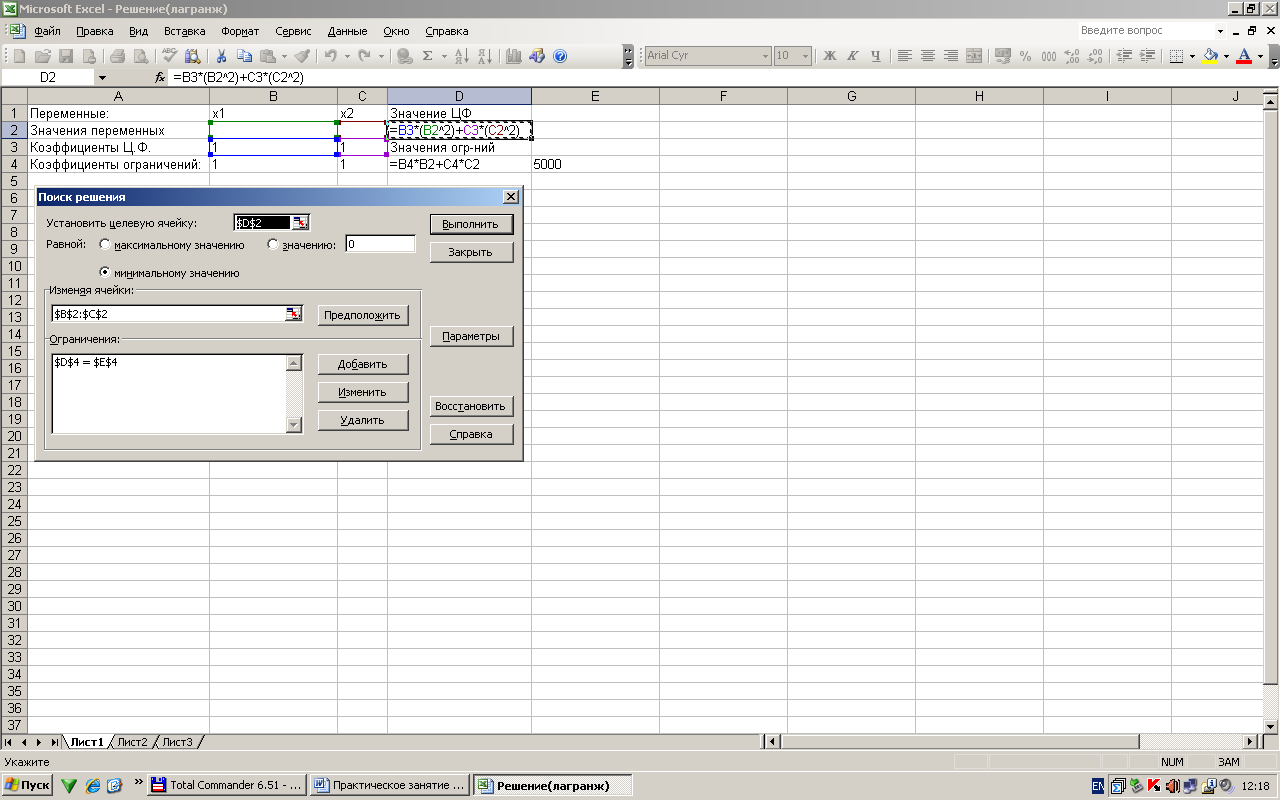
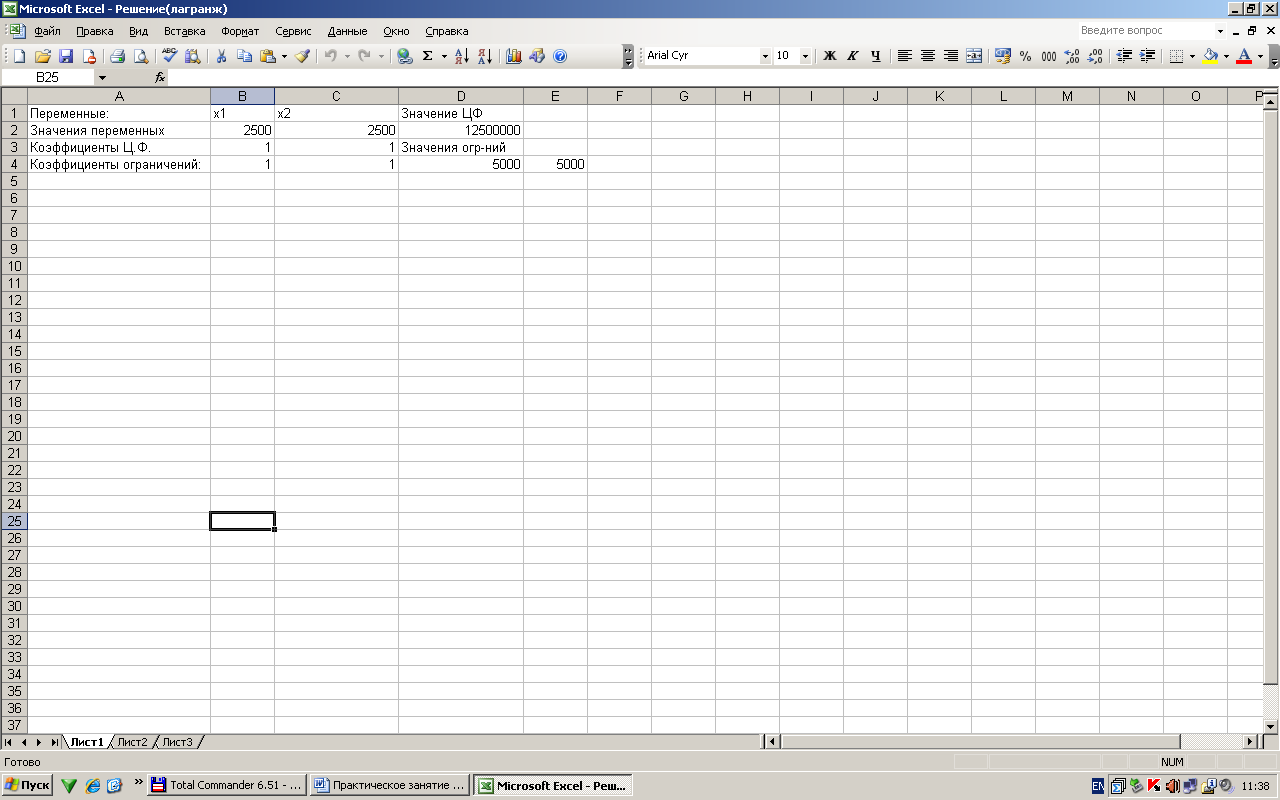
II вариант решения в Exsel
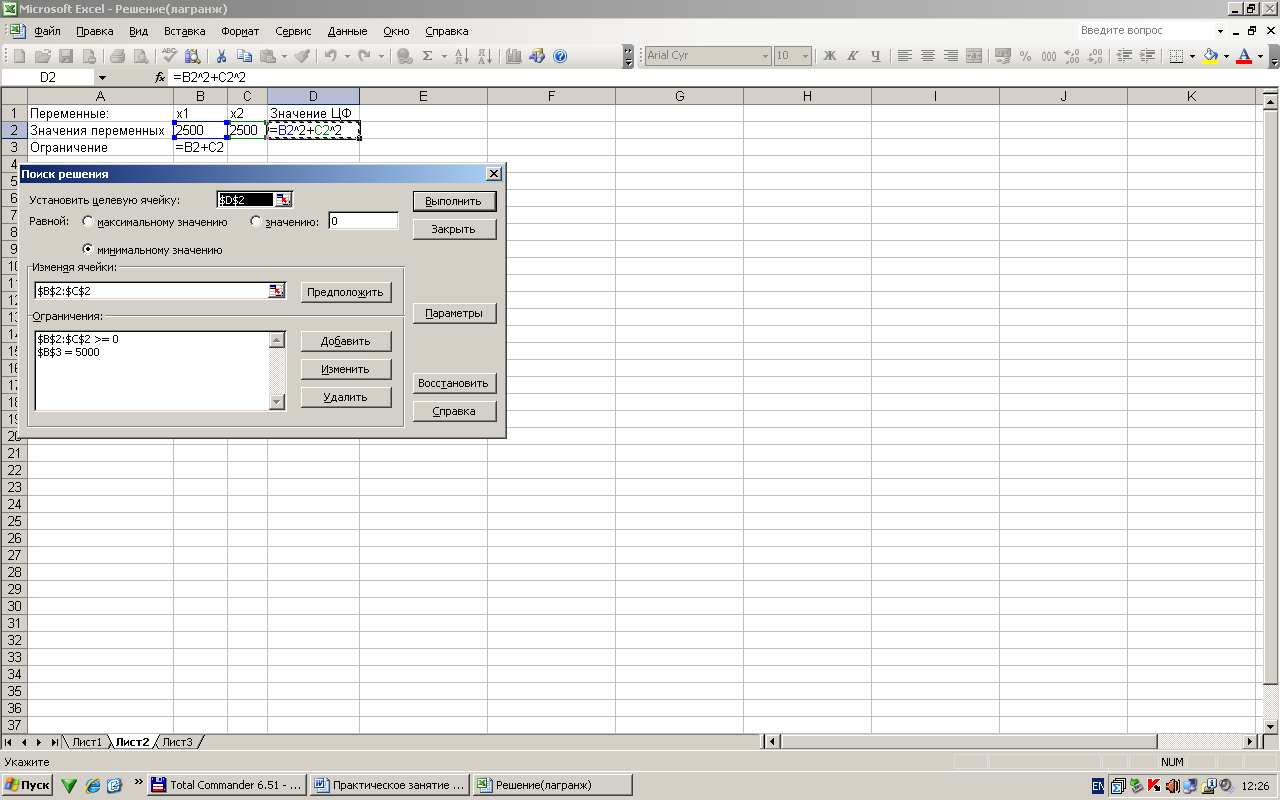
Варианты заданий:
Студопедия рекомендует:
Общественные движения России в первой половине XIX века. Декабристы. Западники и славянофилы. Утопический социализм В первой четверти 19 в. в России зародилась революционная идеология. Микроклимат производственных помещений Микроклимат производственных помещений – это климат внутренней среды данных помещений. ГЛАВА 9. АНАЛИЗ ФИНАНСОВОГО СОСТОЯНИЯ ПРЕДПРИЯТИЯ 9.1. Значение и задачи анализа финансового состояния Предприятия В условиях рыночных отношений исключительно велика роль анализа. Язык — важнейшее средство общения Язык – основное средство общения людей. При помощи языка люди общаются друг с другом. Абсолютная и относительная погрешность вычислений Абсолютная погрешность вычислений находится по формуле: Знак модуля показывает.
Подготовка таблицы
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
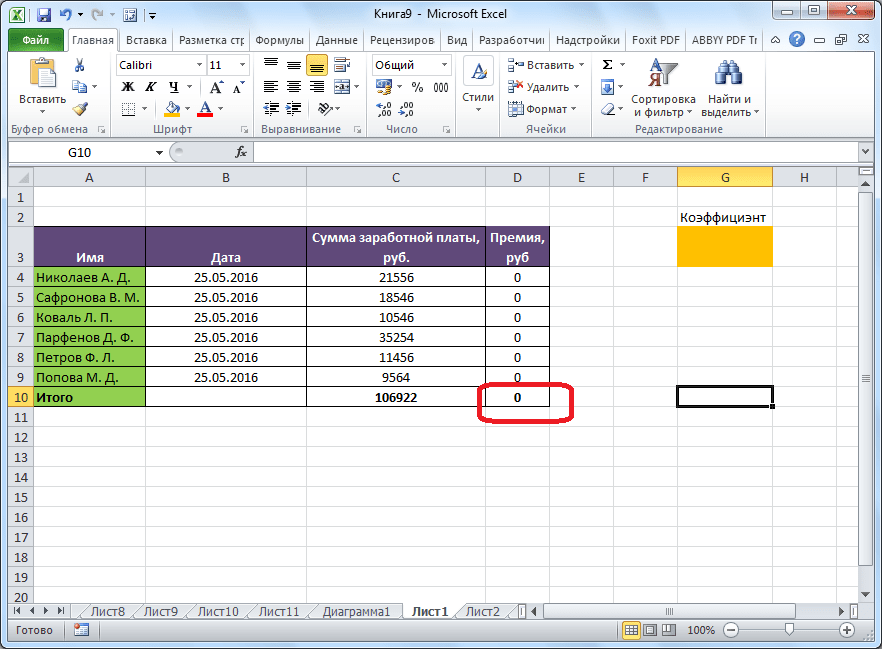
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
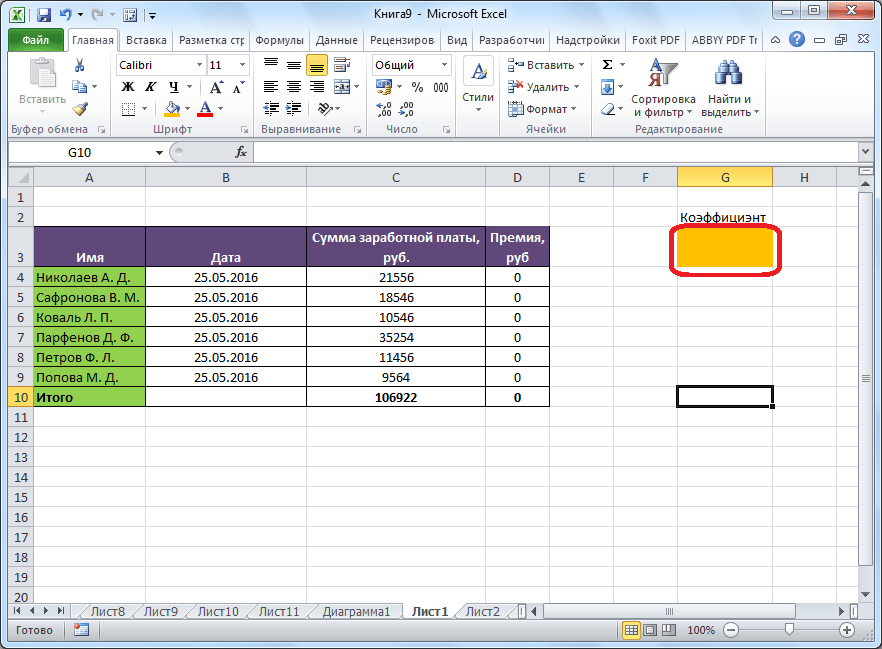
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Загрузка пакета анализа в Excel
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки
Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы
Для удобства также приводим ссылку на оригинал (на английском языке).
Если вам нужно разработать сложные статистические или инженерные анализы, вы можете сэкономить этапы и время с помощью пакета анализа. Вы предоставляете данные и параметры для каждого анализа, и в этом средстве используются соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые инструменты создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
Если вы используете Excel 2007, нажмите кнопку Microsoft Office , а затем – кнопку Параметры Excel.
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
Примечание: Чтобы включить функцию Visual Basic для приложений (VBA) для пакета анализа, вы можете загрузить надстройку » Пакет анализа — VBA » таким же образом, как и при загрузке пакета анализа. В диалоговом окне Доступные надстройки установите флажок Пакет анализа — VBA .
Примечание: Пакет анализа недоступен для Excel для Mac 2011. Дополнительные сведения о том, как найти пакет анализа в Excel для Mac 2011, я не вижу.
Чтобы загрузить пакет анализа в Excel для Mac, выполните указанные ниже действия.
В меню Сервис выберите пункт надстройки Excel.
В окне Доступные надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
Если надстройка Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы найти ее.
Если появляется сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.
Выйдите из приложения Excel и перезапустите его.
Теперь на вкладке Данные доступна команда Анализ данных.
Я не могу найти пакет анализа в Excel для Mac 2011
Существуют несколько сторонних надстроек, которые предоставляют функции пакета анализа для Excel 2011.
Вариант 1. Скачайте статистическое программное обеспечение надстройки КСЛСТАТ для Mac и используйте его в Excel 2011. КСЛСТАТ содержит более 200 основных и расширенных статистических средств, включающих все функции пакета анализа.
Выберите версию КСЛСТАТ, соответствующую операционной системе Mac OS, и загрузите ее.
Откройте файл Excel, содержащий данные, и щелкните значок КСЛСТАТ, чтобы открыть панель инструментов КСЛСТАТ.
В течение 30 дней вы получите доступ ко всем функциям КСЛСТАТ. По истечении 30 дней вы сможете использовать бесплатную версию, включающую функции пакета анализа, или заказать одно из более полных решений КСЛСТАТ.
Вариант 2. Скачайте Статплус: Mac LE бесплатно из Аналистсофт, а затем используйте Статплус: Mac LE с Excel 2011.
Вы можете использовать Статплус: Mac LE для выполнения многих функций, которые ранее были доступны в пакетах анализа, таких как регрессия, гистограммы, анализ вариации (Двухфакторный дисперсионный обработки) и t-тесты.
Перейдите на веб-сайт аналистсофти следуйте инструкциям на странице загрузки.
После загрузки и установки Статплус: Mac LE откройте книгу, содержащую данные, которые нужно проанализировать.
Откройте Статплус: Mac LE. Эти функции находятся в меню Статплус: Mac LE.
В Excel 2011 не входит Справка для Кслстат или Статплус: Mac LE. Справка по Кслстат предоставляется кслстат. Справка для Статплус: Mac LE предоставляется Аналистсофт.
Корпорация Майкрософт не предоставляет поддержку ни для каких продуктов.
Применение Excel для решения нелинейных задач
Нелинейные задачи возникают в различных областях, включая физику, экономику и инженерию. Они включают в себя нелинейные уравнения, которые не могут быть решены с помощью простых аналитических методов. Вместо этого, для их решения можно использовать численные методы, такие как метод оптимизации градиента.
Excel предлагает несколько инструментов для решения нелинейных задач. Один из них — это функции «Goal Seek» и «Solver». Функция «Goal Seek» позволяет находить значения переменных в уравнении, чтобы достичь желаемого результата. Функция «Solver» предоставляет более сложные опции оптимизации, включая оптимизацию градиента.
Оптимизация градиента — это метод численной оптимизации, который использует информацию о градиенте функции для поиска ее минимума или максимума. В Excel, этот метод может быть реализован с помощью функции «Solver».
Для решения нелинейной задачи в Excel, необходимо сначала определить целевую функцию, которую необходимо оптимизировать. Затем, используя функцию «Goal Seek» или «Solver», можно найти значения переменных, которые минимизируют или максимизируют эту функцию.
Однако, при использовании Excel для решения нелинейных задач, следует учитывать его ограничения. Например, некоторые задачи могут быть слишком сложными для решения в Excel, особенно если требуется большое количество переменных или ограничений. Кроме того, Excel может иметь некоторые численные ограничения, которые могут повлиять на точность решения.
В заключение, Excel предоставляет эффективный способ решения нелинейных задач с использованием метода оптимизации градиента. Хотя Excel имеет некоторые ограничения, он все равно является удобным инструментом для быстрого и относительно простого решения нелинейных задач в различных областях.






























